StanFord ML 笔记 第一部分

---

本章节内容：

　　　　1.学习的种类及举例

　　　　2.线性回归，拟合一次函数

　　　　3.线性回归的方法：

　　　　　　　　　　A.梯度下降法--->>>批量梯度下降、随机梯度下降

　　　　　　　　　　B.局部线性回归

　　　　　　　　　　C.用概率证明损失函数(极大似然函数)

---

监督学习：有实际的输入和输出，给出标准答案做参照。比如：回归的运算，下面有例子。

非监督学习：内有标准答案，靠自己去计算。比如：聚类。

梯度下降法：

　　注释：以下直接复制Stanford课程的一位同学评论：super萝卜 [网易北京市海淀区网友]。

　　m代表训练样本的数量，number of training examples； n代表特征的数量（如房屋估价问题中房屋面积，卧室数量为特征，则n=2）； x代表输入变量或者特征，input variables/features； y代表输出变量或目标变量，output variable/target ； variable； （x，y）代表一个样本
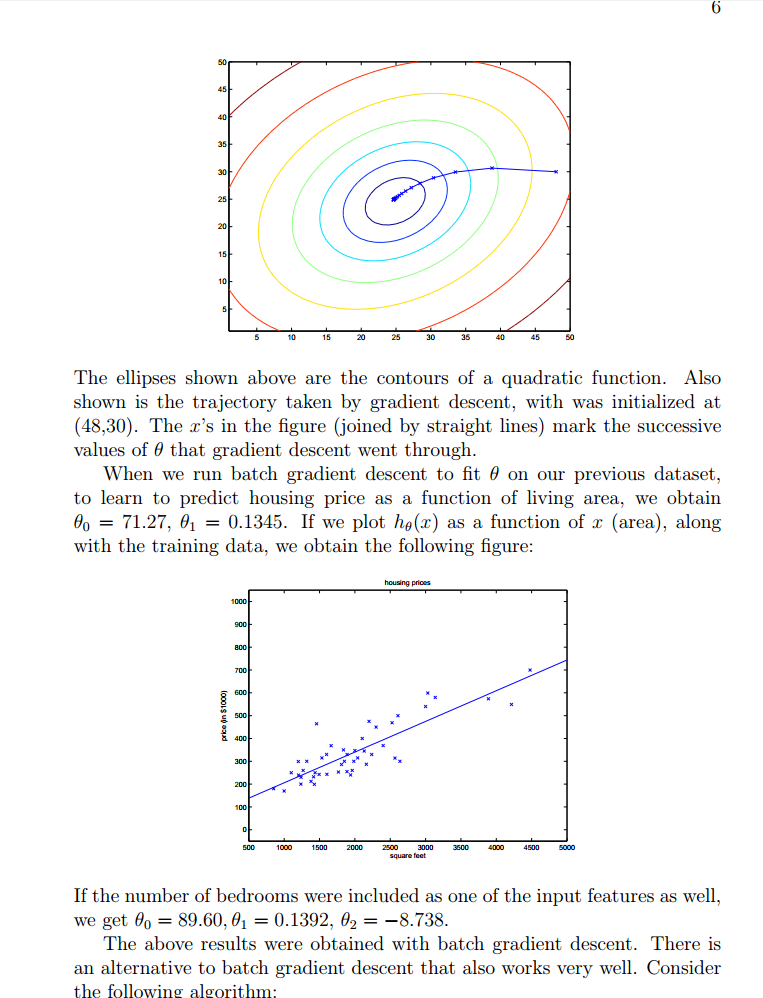
梯度下降的结果有时依赖于参数的初始值。(局部最优问题) 梯度下降法： θj := θj − α ∂(J(θ))/∂θj α：学习速率，控制收敛的速度，过小则需要花费太多时间收敛，过大则可能会跳过最小值部分。 当你接近局部最小值的时候，步子会越来越小，最终直到收敛，当达到局部最小值的时候，梯度值也会为0，所以当越来越接近局部最小值的时候，梯度值也是越来越小，梯度下降的步子也会越来越小。 检测收敛的方法：比较两次迭代的结果，看两次结果是否变化很多，最常见的还是检测J(θ)函数的值，如果该值没有很大变化，则认为达到收敛的效果。 梯度下降算法中，计算的梯度(偏导)，事实上已经是梯度变化最大的方向。 随机梯度下降法：（大数据集合情况下） 并不会精确的收敛到全局最小值。会在最小值周围徘徊，得到近似的全局最小值。
Batch Gradient Descent ——批量梯度下降算法，每次迭代都会遍历整个训练集；不适于数据集很大。 stochastic gradient descent——随机梯度下降算法，每次迭代只会使用训练集的一个样本，比较快，不会精确的收敛到全局的最小值，在最小值附近徘徊。
gradient descent梯度下降 batch gradient descent 批梯度下降 stochastic gradient descent随机梯度下降（incremental gradient descent增量梯度下降）：是对批梯度下降的一种改进，可以不必遍历所有的样本而得出收敛量，速度较快；缺点是无法得出精确的全局最小值；但是得出的收敛值很接近全局最小值，这对我们而言已经足够。
如何检测收敛，一种是检验两次迭代，看两次迭代中是否改变了很多。更多的是检验的值，如果视图最小化的量，不再发生大的改变，就可以认为收敛了。

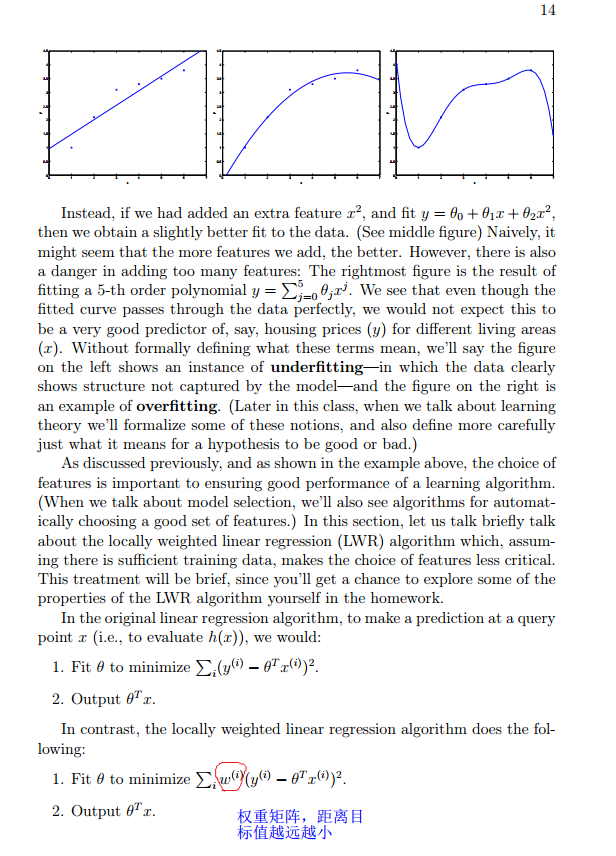
局部线性回归：

　　　　回忆一下高斯滤波比均值滤波的好处？第一：局部性。第二：空间性。局部性在于距离太远就等于没有权重W=0，空间性在于不同的距离权重不一样。

　　　　这篇博文讲的很清楚：http://blog.csdn.net/allenalex/article/details/16370245

中心极限定理：

　　　　设随机变量X1，X2，......Xn，......独立同分布，并且具有有限的数学期望和方差：E(Xi)=μ，D(Xi)=σ20(k=1,2....)，则对任意x，分布函数都符合正太分布。

　　　　该定理说明，当n很大时，随机变量

  

　　　　近似地服从标准正态分布N(0，1)。

　　　　这里的作用是判断一个模型是否可以符合正太分布，下面课程的房价是一个不固定的因素受到天气、人的心情、道路等。。。因素影响，且这些特征都是独立的，所以可以把房价模型假设为正太分布，同时房价-预测=误差，那么误差也就是满足正太N(0,1)分布了。

 似然函数：

　　　　应用在概率函数中，其实和概率函数差不多，就是一个数产生的概率函数，比如：

　　　　

　　　　引申到“最大似然函数”：就是求最大概率下的参数。

　　　　知乎上这个解释感觉很完美：

　　　　最大似然估计：现在已经拿到了很多个样本（你的数据集中所有因变量），这些样本值已经实现，最大似然估计就是去找到那个（组）参数估计值，使得前面已经实现的样本值发生概率最大。因为你手头上的样本已经实现了，其发生概率最大才符合逻辑。这时是求样本所有观测的联合概率最大化，是个连乘积，只要取对数，就变成了线性加总。此时通过对参数求导数，并令一阶导数为零，就可以通过解方程（组），得到最大似然估计值。