GBDT多分类示例

相当于每次都是用2分类，然后不停的训练，最后把所有的弱分类器来进行汇总

样本编号	花萼长度(cm)	花萼宽度(cm)	花瓣长度(cm)	花瓣宽度	花的种类
1	5.1	3.5	1.4	0.2	山鸢尾
2	4.9	3.0	1.4	0.2	山鸢尾
3	7.0	3.2	4.7	1.4	杂色鸢尾
4	6.4	3.2	4.5	1.5	杂色鸢尾
5	6.3	3.3	6.0	2.5	维吉尼亚鸢尾
6	5.8	2.7	5.1	1.9	维吉尼亚鸢尾

Iris数据集

　　这是一个有6个样本的三分类问题。我们需要根据这个花的花萼长度，花萼宽度，花瓣长度，花瓣宽度来判断这个花属于山鸢尾，杂色鸢尾，还是维吉尼亚鸢尾。具体应用到gbdt多分类算法上面。我们用一个三维向量来标志样本的label。[1,0,0] 表示样本属于山鸢尾，[0,1,0] 表示样本属于杂色鸢尾，[0,0,1] 表示属于维吉尼亚鸢尾。

　　gbdt 的多分类是针对每个类都独立训练一个 CART Tree。所以这里，我们将针对山鸢尾类别训练一个 CART Tree 1。杂色鸢尾训练一个 CART Tree 2 。维吉尼亚鸢尾训练一个CART Tree 3，这三个树相互独立。

　　我们以样本 1 为例。针对 CART Tree1 的训练样本是[5.1,3.5,1.4,0.2]，label 是 1，最终输入到模型当中的为[5.1,3.5,1.4,0.2,1]。针对 CART Tree2 的训练样本也是[5.1,3.5,1.4,0.2],但是label 为 0,最终输入模型的为[5.1,3.5,1.4,0.2,0]. 针对 CART Tree 3的训练样本也是[5.1,3.5,1.4,0.2],label 也为0,最终输入模型当中的为[5.1,3.5,1.4,0.2,0]。

　　下面我们来看 CART Tree1 是如何生成的，其他树 CART Tree2 , CART Tree 3的生成方式是一样的。CART Tree的生成过程是从这四个特征中找一个特征做为CART Tree1 的节点。比如花萼长度做为节点。6个样本当中花萼长度 大于5.1 cm的就是 A类，小于等于 5.1 cm 的是B类。生成的过程其实非常简单，问题 1.是哪个特征最合适？ 2.是这个特征的什么特征值作为切分点？ 即使我们已经确定了花萼长度做为节点。花萼长度本身也有很多值。在这里我们的方式是遍历所有的可能性，找到一个最好的特征和它对应的最优特征值可以让当前式子的值最小。

　　

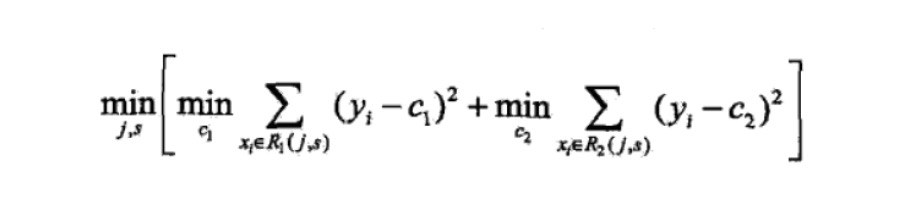
　　我们以第一个特征的第一个特征值为例。R1 为所有样本中花萼长度小于 5.1 cm 的样本集合，R2 为所有样本当中花萼长度大于等于 5.1cm 的样本集合。所以 R1={2}，R2={1,3,4,5,6}.

y1 为 R1 所有样本的label 的均值 1/1=11/1=1。y2 为 R2 所有样本的label 的均值 (1+0+0+0+0)/5=0.2(1+0+0+0+0)/5=0.2。

下面便开始针对所有的样本计算这个式子的值。样本1 属于 R2 计算的值为(1−0.2)², 样本2 属于R1 计算的值为(1−1)2(1−1)2, 样本 3，4，5，6同理都是 属于 R2的 所以值是(0−0.2)². 把这六个值加起来，便是 山鸢尾类型在特征1 的第一个特征值的损失值。这里算出来(1-0.2)²+ (1-1)² + (0-0.2)²+(0-0.2)²+(0-0.2)² +(0-0.2)²= 0.84

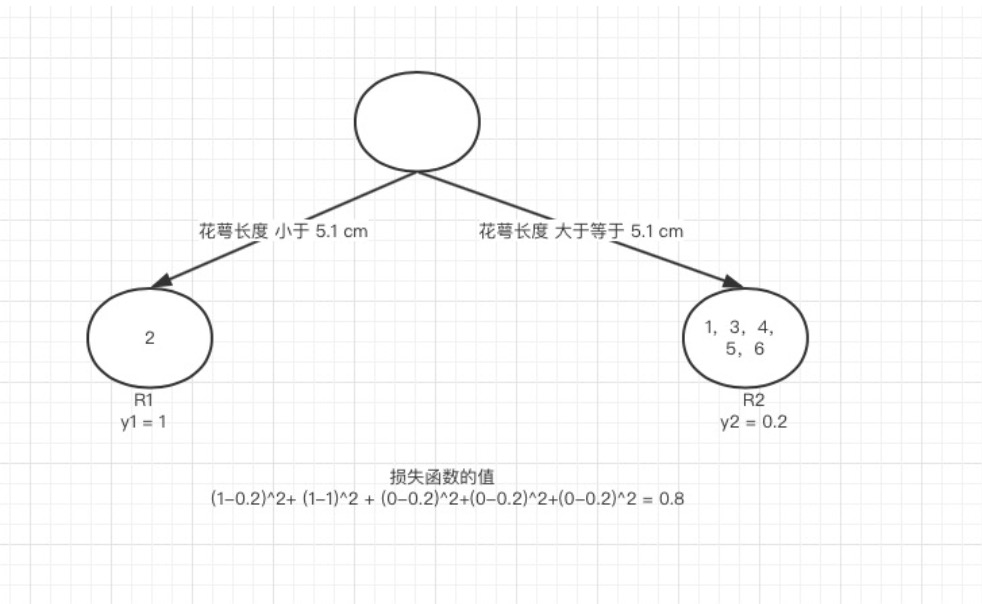
接着我们计算第一个特征的第二个特征值，计算方式同上，R1 为所有样本中 花萼长度小于 4.9 cm 的样本集合，R2 为所有样本当中 花萼长度大于等于 4.9 cm 的样本集合.所以 R1={}，R1={1,2,3,4,5,6}. y1 为 R1 所有样本的label 的均值 = 0。y2 为 R2 所有样本的label 的均值 (1+1+0+0+0+0)/6=0.3333。

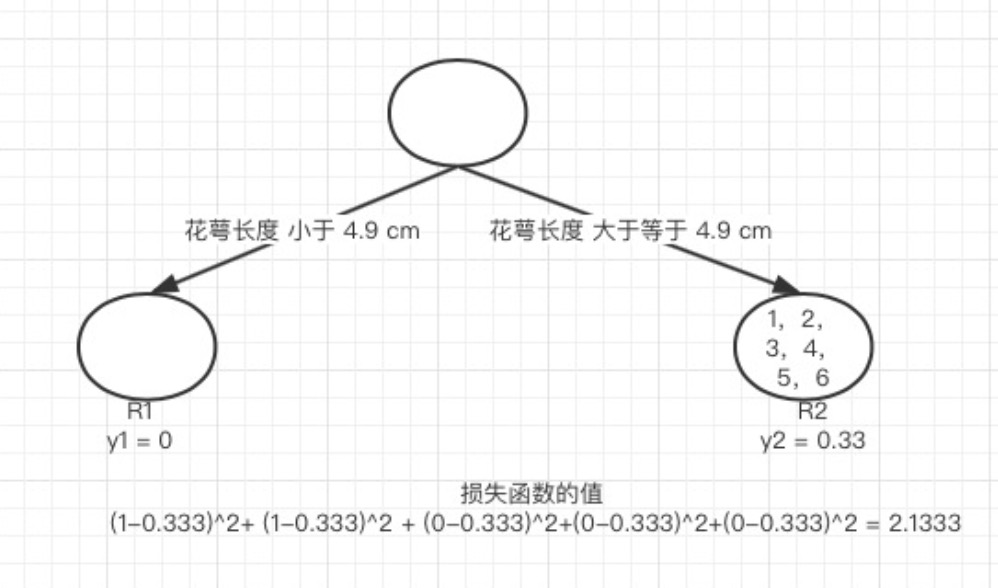
我们需要针对所有的样本,样本1 属于 R2, 计算的值为(1−0.333)², 样本2 属于R2 ,计算的值为(1−0.333)², 样本 3，4，5，6同理都是 属于 R2的, 所以值是(0−0.333)². 把这六个值加起来山鸢尾类型在特征1 的第二个特征值的损失值。这里算出来 (1-0.333)^2+ (1-0.333)^2 + (0-0.333)^2+(0-0.333)^2+(0-0.333)^2 +(0-0.333)^2 = 2.244189. 这里的损失值大于 特征一的第一个特征值的损失值，所以我们不取这个特征的特征值。

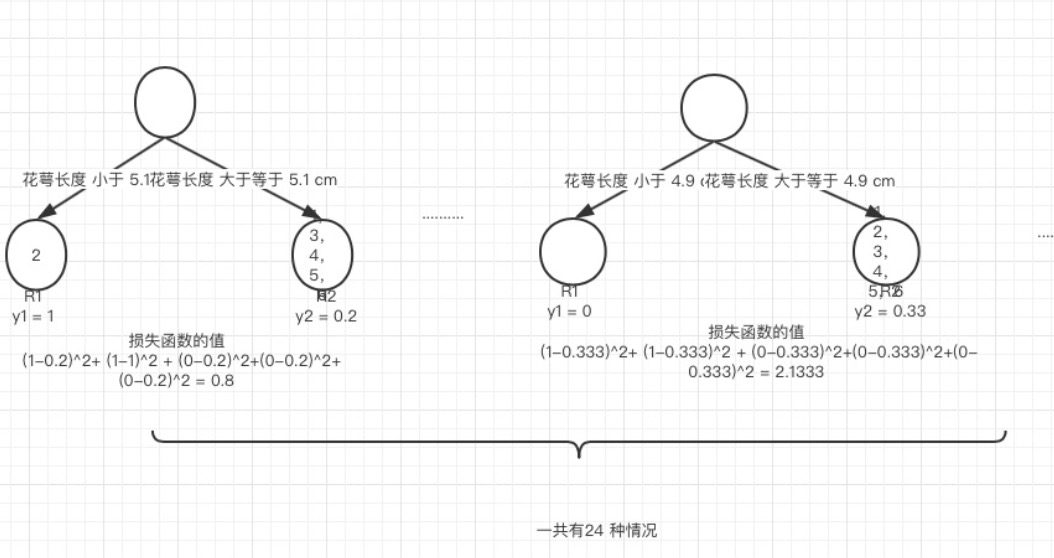
这样我们可以遍历所有特征的所有特征值，找到让这个式子最小的特征以及其对应的特征值，一共有24种情况,4个特征*每个特征有6个特征值。在这里我们算出来让这个式子最小的特征花萼长度,特征值为5.1 cm。这个时候损失函数最小为 0.8。

于是我们的预测函数此时也可以得到:

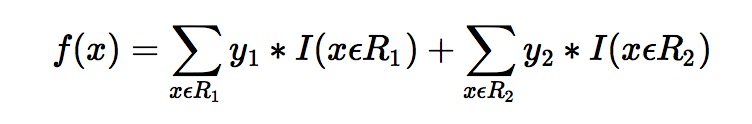
此处 R1 = {2},R2 = {1,3,4,5,6}，y1 = 1,y2 = 0.2。训练完以后的最终式子为

借由这个式子，我们得到对样本属于类别1 的预测值 f1(x)=1+0.2∗5=2f1(x)=1+0.2∗5=2。同理我们可以得到对样本属于类别2,3的预测值f2(x)f2(x),f3(x)f3(x).样本属于类别1的概率 即为