数学图形之罗马曲面(RomanSurface)

罗马曲面,像是一个被捏扁的正四面体.

本文将展示罗马曲面的生成算法和切图,使用自己定义语法的脚本代码生成数学图形.相关软件参见:数学图形可视化工具,该软件免费开源.QQ交流群: 367752815

维基上关于罗马曲面的解释如下:

The Roman surface or Steiner surface (so called because Jakob Steiner was in Rome when he thought of it) is a self-intersecting mapping of the real projective plane into three-dimensional space, with an unusually high degree of symmetry. This mapping is not an immersion of the projective plane; however, the figure resulting from removing six singular points is one.

The simplest construction is as the image of a sphere centered at the origin under the map f(x,y,z) = (yz,xz,xy). This gives an implicitformula of

Also, taking a parametrization of the sphere in terms of longitude (θ) and latitude (φ), gives parametric equations for the Roman surface as follows:

x = r² cos θ cos φ sin φ

y = r² sin θ cos φ sin φ

z = r² cos θ sin θ cos² φ.

罗马曲面脚本代码:

#http://www.ipfw.edu/departments/coas/depts/math/coffman/steinersurface.html
#Steiner's Roman Surface. Three double lines, six pinch points, and a triple point.
#plot3d([r^*sin(t)*cos(t), r*sin(t)*(-r^)^(/), r*cos(t)*(-r^)^(/)], r=.., t=..*Pi, numpoints=)

vertices = D1: D2:
u = from  to (PI) D1
v = from  to (PI) D2

a = sin(u)
b = cos(u)

c = sin(v)
d = cos(v)

r = 5.0

x = r*r*b*d*c
y = r*r*a*d*c
z = r*r*b*a*d*d

我还找到几个与罗马曲面相关的图形

The three double lines of Steiner's Roman Surface coincide

vertices = D1:100 D2:100
t = from 0 to (PI*2) D1
r = from 0 to 1 D2

y = 1-r^2+(r^2)*(sin(t)^2)
x = (r^2)*(sin(t)^2) + 2*(r^2)*sin(t)*cos(t)
z = sqrt((1-r^2)/2) * r * (sin(t)+cos(t))

x = x*5
y = y*5
z = z*5

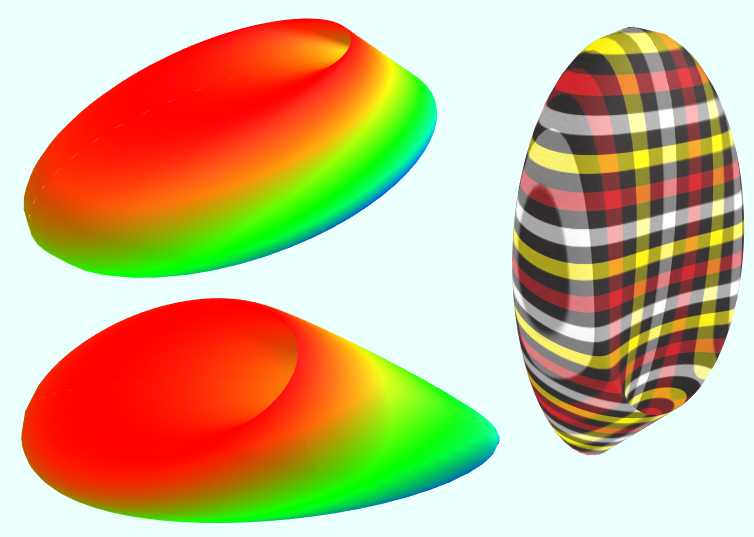
Two of the three double lines in Steiner's Roman Surface

vertices = D1:100 D2:100
t = from 0 to (PI*2) D1
r = from 0 to 1 D2

x = 2*r*cos(t)*sqrt(1-r^2)
y = 2*r*sin(t)*sqrt(1-r^2)
z = 1-2*r*r*(cos(t)^2)

x = x*5
y = y*5
z = z*5