建模算法（三）——非线性规划

一、非线性规划和线性规划不同之处

1、含有非线性的目标函数或者约束条件

2、如果最优解存在，线性规划只能存在可行域的边界上找到（一般还是在顶点处），而非线性规划的最优解可能存在于可行域的任意一点达到。

二、非线性规划的Matlab解法

1、Matlab中非线性规划的数学模型为：

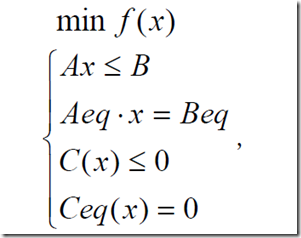
其中f（x）是标量函数，A，B，Aeq，Beq是相应维数的矩阵和向量，C（x），Ceq（X）是非线性向量函数。

然后我们通过一个例子来加深印象

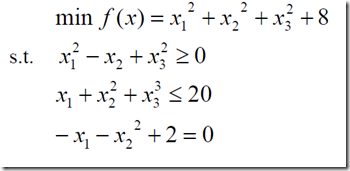
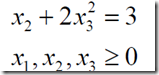
MATLAB实现：

function f=fun1(x)       %定义目标函数
f=sum(x.^2)+8;

function [g,h]=fun2(x)     %非线性约束条件
g=[-x(1)^2+x(2)-x(3)^2
    x(1)+x(2)^2+x(3)^3-20];
h=[-x(1)-x(2)^2+2
    x(2)+2*x(3)^2-3];

options = optimset('largescale','off');
[x,y]=fmincon('fun1',rand(3,1),[],[],[],[],zeros(3,1),[],'fun2',options)  %初始值是个随意的数字

2、求解线性规划的基本迭代格式

（1） 这一块主要是一些概念，认识了这些概念，才能继续理解下面的思想，不得不看，不要觉得烦，就想学加减乘除，我们必须定下’+’就是加这个规则一样，所以我们要理解这些概念。

（2）对于NP问题（非线性规划），可以采用迭代方法求它的最优解。基本思想就是：

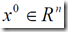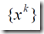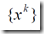从一个选定的初始点出发，按照某一特定的迭代规则产生一个点列，使得当时有穷点列时，其最后一个是NP的最优解；当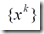时无穷点列是，它存在极限，并且极限点就是NP的最优解

（3）求解NP问题的一般步骤

在列出步骤之前，我们要先理解一个概念（用来决定搜索的最佳方向）

一般步骤为：

a、选取初始点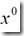，令k：=0

b、构造搜索方向，按照一定的规划，构造f在点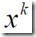处关于K的可行下降方向作为搜索方向。

c、求出下一个迭代点，按迭代格式求出

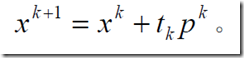
若满足了某种终止条件，就停止迭代

d、用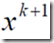代替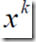，继续迭代。

（4）凸函数、凸规划

这种规划的特点在于，他的局部最优解就是全局最优解，这是很棒的特性，说明这一类的NP问题很容易进行求解。

（二）无约束问题

一、一维搜索方法

例如一维极小化问题，若f(t）是[a,b]区间上的下单峰函数，通过不断地缩短[a,b]的长度，来搜索得到近似最优解。

就是找到关于这个区间对称的2点，然后比较这两点的大小，那么t*肯定将大的那边回缩，构造一个更小的区间来求解，这样的话最后就取到极限值，就可以得到最优解。

1、斐波那契数列法

这个方法就是用来确定步长是如何取得一种方式，是采用斐波那契分数来刻画每次区间的差值。

然后就是经过一系列的探索之后，使最后的探索点和最优解之间的距离不超过精度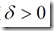，也就是最后的区间长度不能超过这个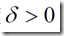，这样子的话，我们可以通过精度，反过来确定需要探索的次数N，进行N次停下来，最终的就是最优解。

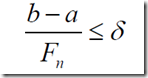
下面是算法的整体思路（编程思路）

2、0.618法（黄金分割法）

只是将比值改为了0.618，这样子的话，编程实现起来更加的简单，只要将上述的第三部中的斐波那契比值改为0.618即可。

3、二次插值法（暂时略过）

4、无约束极值问题的解法

（1）一般格式为：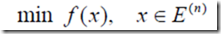

（2）解析法——梯度法

对于基本的迭代格式，我们首先要确定的是搜索方向，那么由微积分的知识可得，沿着负梯度的方向是f下降最快的方向，所以我们作为我们以为搜索的方向。

这个方法的特点就是每次搜索的方向都是下降最快的方向，于是乎我们的停止条件为：

具体步骤如下：

在此举出一个例题

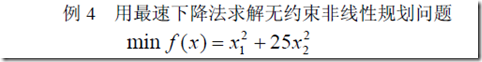
MATLAB实现

function [f,df]=detaf(x)
 
f=x(1)^2+25*x(2)^2;
df=[2*x(1)
    50*x(2)];

x=[2;2];
[f0,g]=detaf(x);
while norm(g)>1e-6
    p=-g/norm(g);
    t=1.0;
    f=detaf(x+t*p);
    while f>f0
        t=t/2;
        f=detaf(x+t*p);
    end
    x=x+t*p;
    [f0,g]=detaf(x);
end
x,f0

最后极值趋近于0，差不多= =。

（3）解析法——牛顿法

其实就是用二次展开式逼近，确定出一个搜索的方向。至于中间的计算（呵呵了- -）

然后一般步骤（编程思路）

然后举一题例题

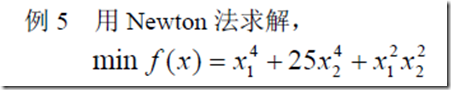
我们可以通过计算得到

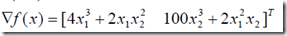
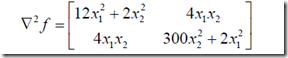
然后使用MATLAB编程求解（其实用C也可以。。）

function [f,df,d2f]=nwfun(x)
 
f=x(1)^4+25*x(2)^4+x(1)^2*x(2)^2;
df=[4*x(1)^3+2*x(1)*x(2)^2
    100*x(2)^3+2*x(1)^2*x(2)];
d2f=[12*x(1)^2+2*x(2)^2,4*x(1)*x(2)
    4*x(1)*x(2),300*x(2)^2+2*x(1)^2];

x=[2;2];
[f0,g1,g2]=nwfun(x);
 
while norm(g1)>0.00001
    p=-inv(g2)*g1;
    x=x+p;
    [f0,g1,g2]=nwfun(x);
end
x,f0

然后如果目标函数不是二次函数，那么一般来说Newton法不能保证求得最优解。

为了提高计算精度，我们在迭代的时候依旧可以使用变步长的方法。

x=[2;2];
[f0,g1,g2]=nwfun(x);
 
while norm(g1)>0.00001
    p=-inv(g2)*g1;
    p=p/norm(p);
    t=1.0;
    f=nwfun(x+t*p);
    while f>f0
       t=t/2;
       f=nwfun(x+t*p)
    end
x=x+t*p;
[f0,g1,g2]=nwfun(x);
end
 
x,f0

（3）解析法——变尺度法

这是用来解决Newton法求逆矩阵太耗时而研究出的一种解决的方法。推到我们可以直接略过吧。

直接写出一般步骤

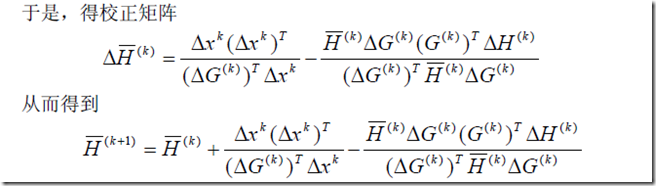
（4）直接法——Powell方法

5、无约束问题的MATLAB方法。。（= =，早说，我都不写了）

1、无约束问题的MATLAB格式

（1）fminunc命令

例子如下

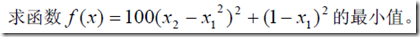
MATLAB调用解题

（2）fminsearch命令

（三）约束极值问题

一、二次规划

1、定义：目标函数是x的二次函数，而且约束条件都是线性的。

2、一般数学模型

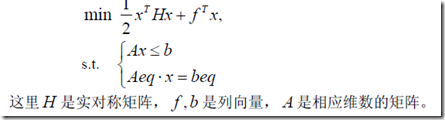
3、MATLAB的求解函数

二、外罚函数法

例题：

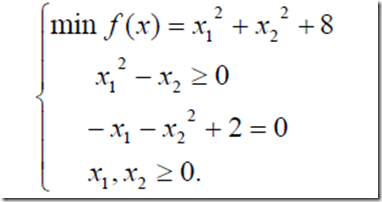
求解

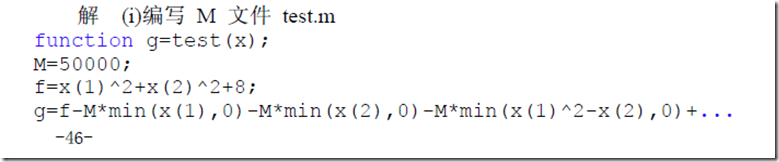
三、MATLAB求约束极值问题

1、fminbnd函数

2、fseminf函数

3、fseminf函数