我们在推导机器学习公式时，常常会用到各种各样的对数，但是奇怪的是--我们往往会忽略对数的底数是谁，不管是2，e，10等。

原因在于，lnx，log2x，log10x，之间是存在常数倍关系。

回顾学过的数学知识，换底公式如下:

　　　　　　　　　　　　　　　　

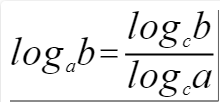
则有

　　　　　　　　　　　　　　　　

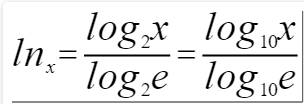
故我们不用纠结对数公式中底数究竟是谁，常数倍关系往往对最后结果不产生影响

【机器学习理论】换底公式--以e，2，10为底的对数关系转化的更多相关文章

  1. Codeforces Gym101502 H.Eyad and Math-换底公式

    H. Eyad and Math   time limit per test 2.0 s memory limit per test 256 MB input standard input outpu ...

  2. 机器学习理论提升方法AdaBoost算法第一卷

    AdaBoost算法内容来自<统计学习与方法>李航,<机器学习>周志华,以及<机器学习实战>Peter HarringTon,相互学习,不足之处请大家多多指教! 提 ...

  3. C语言中 ln（以自然对数e为底） lg(以十为底) 以及logab（以a为底，b为真数）的相关知识

    总所周知,我们在高中学过对数函数,记作y=logax.下面是百度百科关于对数函数的描述: 对数的定义:一般地,如果ax=N(a>0,且a≠1),那么数x叫做以a为底N的对数,记作x=logaN, ...

  4. ACM1229_还是A+B(求A的第K位的数公式:A%((int)(pow(10,K)))

    #include<stdio.h> #include<math.h> int main() { int A,k,B,sum,c,d; while(scanf("%d% ...

  5. 机器学习理论与实战（十）K均值聚类和二分K均值聚类

    接下来就要说下无监督机器学习方法,所谓无监督机器学习前面也说过,就是没有标签的情况,对样本数据进行聚类分析.关联性分析等.主要包括K均值聚类(K-means clustering)和关联分析,这两大类 ...

  6. 机器学习理论与实战（十一）关联规则分析Apriori

    <机器学习实战>的最后的两个算法对我来说有点陌生,但学过后感觉蛮好玩,了解了一般的商品数据关联分析和搜索引擎智能提示的工作原理.先来看看关联分析(association analysis) ...

  7. 机器学习理论知识部分--偏差方差平衡（bias-variance tradeoff）

    摘要: 1.常见问题 1.1 什么是偏差与方差? 1.2 为什么会产生过拟合,有哪些方法可以预防或克服过拟合? 2.模型选择例子 3.特征选择例子 4.特征工程与数据预处理例子 内容: 1.常见问题 ...

  8. 机器学习理论之SVM

    支持向量机系列 (1) 算法理论理解 http://blog.pluskid.org/?page_id=683 手把手教你实现SVM算法(一) (2) 算法应用 算法应用----python 实现实例 ...

  9. [机器学习理论] 降维算法PCA、SVD(部分内容，有待更新)

    几个概念 正交矩阵 在矩阵论中,正交矩阵(orthogonal matrix)是一个方块矩阵,其元素为实数,而且行向量与列向量皆为正交的单位向量,使得该矩阵的转置矩阵为其逆矩阵:  其中,为单位矩阵. ...

随机推荐

  1. qt中用tcp传输xml消息 good

    本文博客链接:http://blog.csdn.net/jdh99,作者:jdh,转载请注明.   环境: 主机:WIN7 开发环境:Qt5 3.1.2 说明: 在tcp上传输xml消息. 协议格式如 ...

  2. windows service 之访问权限（有NetworkService和LocalSystem的区分）

    最近写了一个关于从局域网的算机上下载文件的winodws service,最初认为应该没什么大的问题.通过本地的调试也没发现问题.但是当我把程序发布后发现服务报错“访问路径被拒绝”,我的第一感觉,肯定 ...

  3. cookie,session,用户认证组件

    一. 绘画跟踪技术 在客户端与服务端的一次会务中,多次的请求与相应,HTTP协议是无状态协议,也就是说每个请求都是独立的!无法记录前一次请求的状态.会话跟踪技术即能够实现多次回话间信息共享的作用,HT ...

  4. Kafka笔记3

    向Kafka写入消息从创建一个ProducerRecord对象开始,ProducerRecord需要包含目标主题和要发送的内容,我们还可以指定键或分区,在发送ProducerRecord对象时,生产者 ...

  5. ZooKeeper学习第三期---Zookeeper命令操作（转）

    转载来源:https://www.cnblogs.com/sunddenly/p/4031881.html 一.Zookeeper的四字命令 Zookeeper支持某些特定的四字命令字母与其的交互.他 ...

  6. SpringCloud Sleuth入门介绍

    案例代码:https://github.com/q279583842q/springcloud-e-book 一.Sleuth介绍   为什么要使用微服务跟踪?它解决了什么问题? 1.微服务的现状? ...

  7. C++程序设计1（侯捷video 1-6）

    一.头文件的防御式声明(video2) #ifndef __COMPLEX__ #define __COMPLEX__ //内容 #endif 二.初步感受模板(video2) 定义的时候: //复数 ...

  8. eclipse下jdbc数据源与连接池的配置及功能简介

    今天在做四则运算网页版的时候遇到了一个困惑,由于需要把每个产生的式子存进 数据库,所以就需要很多次重复的加载驱动,建立连接等操作,这样一方面写程序不方便,加大了程序量,另一方面,还有导致数据库的性能急 ...

  9. asp.net core 系列之Dependency injection(依赖注入)

    这篇文章主要讲解asp.net core 依赖注入的一些内容. ASP.NET Core支持依赖注入.这是一种在类和其依赖之间实现控制反转的一种技术(IOC). 一．依赖注入概述 1.原始的代码 依赖 ...

  10. 常用的方法论-5why