【Luogu P3384】树链剖分模板

树链剖分的基本思想是把一棵树剖分成若干条链，再利用线段树等数据结构维护相关数据，可以非常暴力优雅地解决很多问题。

树链剖分中的几个基本概念：

重儿子：对于当前节点的所有儿子中，子树大小最大的一个儿子就是重儿子（子树大小相同的则随意取一个）

轻儿子：不是重儿子就是轻儿子

重边：连接父节点和重儿子的边

轻边：连接父节点和轻儿子的边

重链：相邻重边相连形成的链

值得注意的还有以下几点：

叶子节点没有重儿子也没有轻儿子；

对于每一条重链，其起点必然是轻儿子；

单独一个轻叶子节点也是一条重链；

结合上面三条可以得出树剖的一个性质：重链必然可以囊括所有的节点。



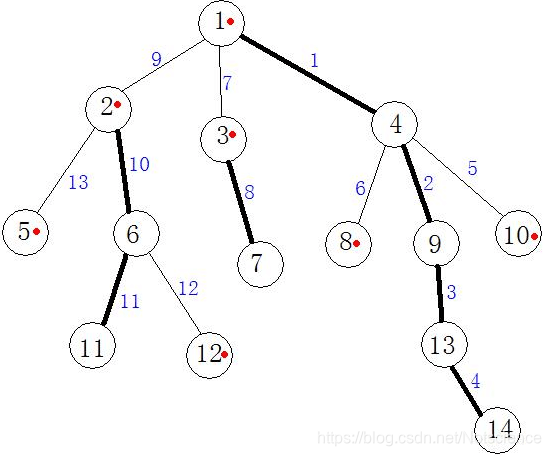
（图片来源百度图片，侵删）

红点标记的是轻儿子，粗线就是重链。结合图片理解概念。

树链剖分需要怎么做呢？

1、用DFS给每一个节点标记深度，父节点和重儿子。

2、用DFS按照DFS遍历的顺序给每一个节点标记新的编号。关键点：先处理重儿子再处理轻儿子

解释：先处理重儿子可以让重链上的每一个点的编号连续。可以观察上图，线上的数字就是DFS的顺序。使编号连续后，我们就可以使用线段树来维护数据了。

做完以上两步就算是完成了树链剖分了，接下来要做的就是利用其它数据结构来进行维护了。

void add(ll sta,ll to)
{
	edge[++cnt].to=to;
	edge[cnt].next=head[sta];
	head[sta]=cnt;
}//链式前向星存树
void dfs1(ll now,ll fa,ll deep)
{
	f[now]=fa;//记录父节点
	d[now]=deep;//记录深度（深度在区间求和时会用到）
	size[now]=1;//记录子树大小
	for (ll i=head[now];i!=0;i=edge[i].next)
	{
		if (edge[i].to==fa) continue;
		dfs1(edge[i].to,now,deep+1);
		size[now]+=size[edge[i].to];
		if (size[edge[i].to]>size[wson[now]]) wson[now]=edge[i].to;
		//取重儿子
	}
}
void dfs2(ll now,ll t)
{
	top[now]=t;//记录节点所在重链的起点
	id[now]=++cnt;//按照顺序编号
	rk[cnt]=now;//记录第cnt个点表示的是now节点，建树时会用到
	if (wson[now]) dfs2(wson[now],t);//优先处理重儿子
	for (ll i=head[now];i!=0;i=edge[i].next)
	{
		if (edge[i].to==wson[now]) continue;
		if (edge[i].to==f[now]) continue;
		dfs2(edge[i].to,edge[i].to);//一条重链的开头必然是轻儿子，链头即为它本身
	}
}

树上两点的最短路径修改操作：

void treeupd(ll x,ll y,ll num)
{
	while (top[x]!=top[y])
	{
		if (d[top[x]]>d[top[y]])
		{
			segupd(1,1,n,id[top[x]],id[x],num);
			//segupd为线段树的更新函数
			x=f[top[x]];
		}
		else
		{
			segupd(1,1,n,id[top[y]],id[y],num);
			//segupd为线段树的更新函数
			y=f[top[y]];
		}
	}
	//这一个循环的目的是，只要这两个节点不在一条重链上，
	//就让比较深的那一个往上跳到另一条链直到两者在同一条链上
	//又因为节点编号是连续的，所以可以很方便地给整条链加上修改操作
	if (id[x]<=id[y]) segupd(1,1,n,id[x],id[y],num);
	else segupd(1,1,n,id[y],id[x],num);
	//在最后两者位于同一条链上后，仍然要对他们两个之间的节点进行修改。
}

求和操作不再赘述，与上面的更新操作类似。

完整代码

#include<cstdio>
#include<algorithm>
#define lson root<<1
#define rson root<<1|1
#define ll long long
#define mid ((l+r)>>1)
using namespace std;
struct data
{
	ll to,next;
}edge[200005];
ll cnt,head[200005],f[100005],d[100005],size[100005],wson[100005],top[100005],id[100005];
ll rk[100005],tree[800005],n,m,a[100005],p,tag[800005],r,x,y,z,flag;
void add(ll sta,ll to)
{
	edge[++cnt].to=to;
	edge[cnt].next=head[sta];
	head[sta]=cnt;
}
void dfs1(ll now,ll fa,ll deep)
{
	f[now]=fa;
	d[now]=deep;
	size[now]=1;
	for (ll i=head[now];i!=0;i=edge[i].next)
	{
		if (edge[i].to==fa) continue;
		dfs1(edge[i].to,now,deep+1);
		size[now]+=size[edge[i].to];
		if (size[edge[i].to]>size[wson[now]]) wson[now]=edge[i].to;
	}
}
void dfs2(ll now,ll t)
{
	top[now]=t;
	id[now]=++cnt;
	rk[cnt]=now;
	if (wson[now]) dfs2(wson[now],t);
	for (ll i=head[now];i!=0;i=edge[i].next)
	{
		if (edge[i].to==wson[now]) continue;
		if (edge[i].to==f[now]) continue;
		dfs2(edge[i].to,edge[i].to);
	}
}
void build(ll root,ll l,ll r)
{
	if (l==r)
	{
		tree[root]=a[rk[l]]%p;
		return ;
	}
	build(lson,l,mid);
	build(rson,mid+1,r);
	tree[root]=(tree[lson]+tree[rson])%p;
}
void push_down(ll root,ll l,ll r)
{
	if (tag[root]==0) return ;
	tag[lson]+=tag[root];
	tag[rson]+=tag[root];
	tree[lson]+=tag[root]*(mid-l+1);
	tree[rson]+=tag[root]*(r-mid);
	tag[lson]%=p;
	tag[rson]%=p;
	tree[lson]%=p;
	tree[rson]%=p;
	tag[root]=0;
}
void segupd(ll root,ll l,ll r,ll al,ll ar,ll num)
{
	if (ar<l||r<al) return ;
	if (al<=l&&r<=ar)
	{
		tree[root]+=num*(r-l+1);
		tag[root]+=num;
		tree[root]%=p;
		tag[root]%=p;
		return ;
	}
	push_down(root,l,r);
	segupd(lson,l,mid,al,ar,num);
	segupd(rson,mid+1,r,al,ar,num);
	tree[root]=(tree[lson]+tree[rson])%p;
}
ll query(ll root,ll l,ll r,ll al,ll ar)
{
	if (ar<l||r<al) return 0;
	if (al<=l&&r<=ar) return tree[root]%p;
	push_down(root,l,r);
	return (query(lson,l,mid,al,ar)+query(rson,mid+1,r,al,ar))%p;
}
ll getsum(ll x,ll y)
{
	ll sum=0;
	while (top[x]!=top[y])
	{
		if (d[top[x]]>d[top[y]])
		{
			sum=(sum+query(1,1,n,id[top[x]],id[x]))%p;
			x=f[top[x]];
		}
		else
		{
			sum=(sum+query(1,1,n,id[top[y]],id[y]))%p;
			y=f[top[y]];
		}
	}
	if (id[x]<=id[y]) sum=(sum+query(1,1,n,id[x],id[y]))%p;
	else sum=(sum+query(1,1,n,id[y],id[x]))%p;
	return sum;
}
void treeupd(ll x,ll y,ll num)
{
	while (top[x]!=top[y])
	{
		if (d[top[x]]>d[top[y]])
		{
			segupd(1,1,n,id[top[x]],id[x],num);
			x=f[top[x]];
		}
		else
		{
			segupd(1,1,n,id[top[y]],id[y],num);
			y=f[top[y]];
		}
	}
	if (id[x]<=id[y]) segupd(1,1,n,id[x],id[y],num);
	else segupd(1,1,n,id[y],id[x],num);
}
int main()
{
	scanf("%lld%lld%lld%lld",&n,&m,&r,&p);
	for (ll i=1;i<=n;i++)
		scanf("%lld",&a[i]);
	for (ll i=1;i<n;i++)
	{
		scanf("%lld%lld",&x,&y);
		add(x,y);
		add(y,x);
	}
	cnt=0;
	dfs1(r,0,0);
	dfs2(r,r);
	build(1,1,n);
	for (ll i=1;i<=m;i++)
	{
		scanf("%lld",&flag);
		if (flag==1)
		{
			scanf("%lld%lld%lld",&x,&y,&z);
			treeupd(x,y,z);
		}
		if (flag==2)
		{
			scanf("%lld%lld",&x,&y);
			printf("%lld\n",getsum(x,y));
		}
		if (flag==3)
		{
			scanf("%lld%lld",&x,&z);
			segupd(1,1,n,id[x],id[x]+size[x]-1,z);
			//这里可以结合图片理解一下为什么。
		}
		if (flag==4)
		{
			scanf("%lld",&x);
			printf("%lld\n",query(1,1,n,id[x],id[x]+size[x]-1));
		}
	}
	return 0;
}

练习题：

NOI2015软件包管理器

HAOI2015树上操作

ZJOI2008树的统计