浅谈无旋treap(fhq_treap)

一、简介

无旋Treap（fhq_treap），是一种不用旋转的treap，其代码复杂度不高，应用范围广（能代替普通treap和splay的所有功能），是一种极其强大的平衡树。

无旋Treap是一个叫做范浩强的大佬发明的（快%啊！）

在我们一起学习无旋Treap之前，本蒟蒻有几句活想说：

1.无旋Treap我个人认为是最容易理解的一种平衡树，而且编程复杂度不高，功能还那么强大。

　我一开始学平衡树的时候是先从普通的带旋转的Treap开始学的。那种Treap，我现在都没搞懂什么左旋右旋究竟是怎么一回事。

　我当时真的以为我这辈子都不指望学会平衡树了，直到djq大佬（快%！）告诉了我这种很美妙的数据结构。

　我真就不明白了，为什么那么多人愿意去学普通的Treap而不学无旋Treap。无旋Treap更容易理解，最主要的是他与普通的Treap相比能可持久化！（尽管我不会）

　所以，在大家学习完无旋Treap以后，本蒟蒻请诸君不妨推广一下无旋Treap，造福更多的Oier。

　2.关于无旋Treap和其他平衡树的比较：（这个建议大家学完无旋Treap再来看，可能感触会更深刻一些）

　　与AVL相比：旋转操作真的很浪费时间，最坏情况下复杂度为O(log n)，而且AVL树难写无比，不适合运用于算法竞赛。

　　与普通Treap相比：参见第一条

　　与splay相比：基本上可以代替splay的所有功能，但是在处理LCT问题上没有splay优秀

　　与rbt（红黑树相比）：红黑树特别难写是众所周知的。

　　与sbt相比：sbt是我认为的最强大的平衡树。但是无旋Treap中的merge、split操作的应用的广泛（可持久化Treap维护Hash之类的）是sbt做不到的。

二、Treap

　　什么是Treap？

　　Treap=Tree+heap

　　相信大家都知道二叉堆吧。父节点的权值比子节点都要大（或小）

　　而Treap，则是在BST（二叉查找树）的基础上，添加二叉堆中的这个元素。

　　Treap与heap的区别是，heap是完全二叉树，而Treap不是。

　　下面的

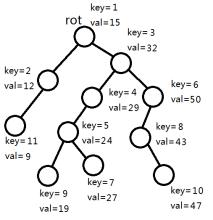
三、核心操作

我在前面说过，普通的Treap最烦人的地方便是旋转。

而无旋Treap是如何做到无旋的呢？

关键就在两个操作：merge和split

1.split

　split,顾名思义，就是把一个平衡树分成两棵树。

　split有两种：一种是按照权值split，一种是按照size来split。

　如果按照权值split，那么分出来两棵树的第一棵树上的每一个数的大小都小于（或小于等于，视具体情况而定）x;

　如果按照size split，那么分出来两棵树的第一棵树恰好有x个节点。

　我们可以结合具体代码讲解：　

inline void split(int k,int& l,int& r,int x){//理解时，我们可以把l当做是答案的第一个，r当做答案的第二个，这个函数的意义是：将以k为根的树按照val分为以l为根的树和以r为根的树。注意引用的作用
    if(!k){
        l=r=;//分到底了，返回
        return;
    }
    if(tree[k].val<x){//如果比它小
        l=k;//那么x肯定在k的右子树里，先将k贴到第一个答案上
        split(tree[l].r,tree[l].r,r,x);//把第一个答案的右子树按x分开，得到答案（这里自己理解一下，不难懂）
    }else{//反之亦然
        r=k;
        split(tree[r].l,l,tree[r].l,x);
    }
    push_up(k);
}

　　而按size split的道理是一样的：

inline void split(int k,int& l,int& r,int x){
    if(!k){
        l=r=;
        return;
    }
    if(tree[tree[k].l].size+<=x){
        l=k;
        split(tree[l].r,tree[l].r,r,x-tree[tree[k].l].size-);//注意这里有些变化
    }else{
        r=k;
        split(tree[r].l,l,tree[r].l,x);
    }
    push_up(k);
}

这样就把一棵树分开了。

2.merge

　merge就是把两颗原本分开的树合并在一起。

　我们仍然结合具体代码讲解

inline void merge(int& k,int l,int r){//函数名的意义是：把以l为根的树和以r为根的树合并为以k为根的树
    if(!l||!r){//合并到底，返回
        k=l+r;
        return;
    }
    if(tree[l].p>tree[r].p){//默认大根堆
        k=l;//先把l挂到k上
        merge(tree[k].r,tree[k].r,r);//注意要满足BST性质
    }else{//反之亦然
        k=r;
        merge(tree[k].l,l,tree[k].l);
    }
    push_up(k);
} 

　有了merge和split，其他平衡树的基本操作就好做多了

三、其他操作

inline void insert(int val){
    int x,y;
    split(root,x,y,val-);
    merge(x,x,New(val));
    merge(root,x,y);
}
inline void Delete(int val){
    int x,y,z;
    split(root,x,y,val);
    split(x,x,z,val-);
    merge(z,tree[z].l,tree[z].r);
    merge(x,x,z);
    merge(root,x,y);
}
inline int rnk(int val){
    int x,y;
    split(root,x,y,val-);
    int ans=tree[x].size+;
    merge(root,x,y);
    return ans;
}
inline int kth(int k){
    int x=root;
    while(true){
        if(k==tree[tree[x].l].size+) return tree[x].val;
        if(k<=tree[tree[x].l]) x=tree[x].l;
        else k-=tree[tree[x].l].size+,x=tree[x].r;
    }
}
inline int pre(int val){
    int x,y;
    split(root,x,y,val-);
    int ans=tree[x].val;
    merge(root,x,y);
    return ans;
}
inline int suf(int val){
    int x,y;
    split(root,x,y,val);
    int ans=kth(tree[x].size+);
    merge(root,x,y);
    return ans;
}

最后给大家放上一道模板题P3369 【模板】普通平衡树

如有不足请指正，谢谢