ZJOI2012网络 题解报告【LCT】

题目描述

有一个无向图G，每个点有个权值，每条边有一个颜色。这个无向图满足以下两个条件：

1. 对于任意节点连出去的边中，相同颜色的边不超过两条。

2. 图中不存在同色的环，同色的环指相同颜色的边构成的环。

在这个图上，你要支持以下三种操作：

1. 修改一个节点的权值。

2. 修改一条边的颜色。

3. 查询由颜色c的边构成的图中，所有可能在节点u到节点v之间的简单路径上的节点的权值的最大值。

输入输出格式

输入格式：

输入文件network.in的第一行包含四个正整数N, M, C, K，其中N为节点个数，M为边数，C为边的颜色数，K为操作数。

接下来N行，每行一个正整数vi，为节点i的权值。

之后M行，每行三个正整数u, v, w，为一条连接节点u和节点v的边，颜色为w。满足1 ≤ u, v ≤ N，0 ≤ w < C，保证u ≠ v，且任意两个节点之间最多存在一条边(无论颜色)。

最后K行，每行表示一个操作。每行的第一个整数k表示操作类型。

1. k = 0为修改节点权值操作，之后两个正整数x和y，表示将节点x的权值vx修改为y。

2. k = 1为修改边的颜色操作，之后三个正整数u, v和w，表示将连接节点u和节点v的边的颜色修改为颜色w。满足0 ≤ w < C。

3. k = 2为查询操作，之后三个正整数c, u和v，表示查询所有可能在节点u到节点v之间的由颜色c构成的简单路径上的节点的权值的最大值。如果不存在u和v之间不存在由颜色c构成的路径，那么输出“-1”。

输出格式：

输出文件network.out包含若干行，每行输出一个对应的信息。

1. 对于修改节点权值操作，不需要输出信息。

2. 对于修改边的颜色操作，按以下几类输出：

a) 若不存在连接节点u和节点v的边，输出“No such edge.”。

b) 若修改后不满足条件1，不修改边的颜色，并输出“Error 1.”。

c) 若修改后不满足条件2，不修改边的颜色，并输出“Error 2.”。

d) 其他情况，成功修改边的颜色，并输出“Success.”。

输出满足条件的第一条信息即可，即若同时满足b和c，则只需要输出“Error 1.”。

1. 对于查询操作，直接输出一个整数。

输入输出样例

输入样例#1：

4 5 2 7
1
2
3
4
1 2 0
1 3 1
2 3 0
2 4 1
3 4 0
2 0 1 4
1 1 2 1
1 4 3 1
2 0 1 4
1 2 3 1
0 2 5
2 1 1 4

输出样例#1：

4
Success.
Error 2.
-1
Error 1.
5

说明

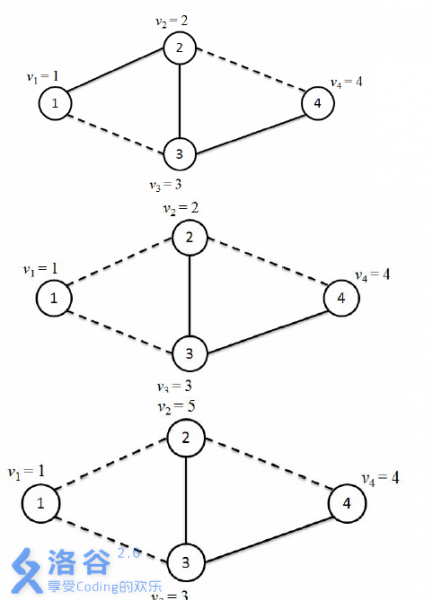
颜色0为实线的边，颜色1为虚线的边，

由颜色0构成的从节点1到节点4的路径有1 – 2 – 4，故max{v1, v2, v4} = max{ 1, 2, 4 } = 4。

将连接节点1和节点2的边修改为颜色1，修改成功，输出“Success.”

将连接节点4和节点3的边修改为颜色1，由于修改后会使得存在由颜色1构成的环( 1 – 2 – 4 – 3 – 1 )，不满足条件2，故不修改，并输出“Error 2”。

不存在颜色0构成的从节点1到节点4的边，输出“-1”。

将连接节点2和节点3的边修改为颜色1，由于修改后节点2的连出去的颜色为1的边有3条，故不满足条件1，故不修改，并输出“Error 1.”。

将节点2的权值修改为5。

由颜色1构成的从节点1到节点4的路径有 1 – 2 – 4，故max{v1, v2, v4} = max{ 1, 5, 4 } = 5。

【数据规模】

对于30%的数据：N ≤ 1000，M ≤ 10000，C ≤ 10，K ≤ 1000。

另有20%的数据：N ≤ 10000，M ≤ 100000，C = 1，K ≤ 100000。

对于100%的数据：N ≤ 10000，M ≤ 100000，C ≤ 10，K ≤ 100000。

题解

题目拿来一看，路径唯一，那么对于每种颜色就是一棵树，而且是动态的树，颜色改变就相当于断边与连边

很自然就想到对于每种颜色各建一棵LCT

很方地往下看数据范围。。。。nice√最多也就10种颜色，完全可以承受

由于一个节点的边最多两条，可以将它存下来，每次修改颜色时暴力查找就好了，不用想太多。。

【修改颜色甚至有可能是原来的颜色= =，忽略这个就才20分。。。加上一句特判就A了。。。扯淡吧。。】

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define LL long long int
#define isr(u,c) (e[c][e[c][u].f].ch[1] == u)
#define isrt(u,c) (!e[c][u].f || (e[c][e[c][u].f].ch[0] != u && e[c][e[c][u].f].ch[1] != u))
using namespace std;
const int maxn = 10005,maxm = 100005,INF = 200000000;

inline int read(){
	int out = 0,flag = 1;char c = getchar();
	while (c < 48 || c > 57) {if (c == '-') flag = -1; c = getchar();}
	while (c >= 48 && c <= 57) {out = out * 10 + c - 48; c = getchar();}
	return out * flag;
}

int N,M,C,K,temp[maxn];
int edge[maxn][11][3];

struct node{
	int w,f,ch[2],rev,Max;
	node() {f = ch[0] = ch[1] = rev = 0;}
}e[11][maxn];

inline void push_up(int u,int c){
	e[c][u].Max = max(e[c][u].w,max(e[c][e[c][u].ch[0]].Max,e[c][e[c][u].ch[1]].Max));
}

inline void pd(int u,int c){
	if (e[c][u].rev){
		swap(e[c][u].ch[0],e[c][u].ch[1]);
		e[c][e[c][u].ch[0]].rev ^= 1;
		e[c][e[c][u].ch[1]].rev ^= 1;
		e[c][u].rev = 0;
	}
}

inline void push_down(int u,int c){
	int i = 0;
	do {temp[++i] = u;} while(!isrt(u,c) && (u = e[c][u].f));
	while (i) pd(temp[i--],c);
}

inline int Find(int u,int c){
	while (e[c][u].f) u = e[c][u].f;
	return u;
}

inline void spin(int u,int c){
	int s = isr(u,c),fa = e[c][u].f;
	e[c][u].f = e[c][fa].f;
	if(!isrt(fa,c)) e[c][e[c][fa].f].ch[isr(fa,c)] = u;
	e[c][fa].ch[s] = e[c][u].ch[s^1];
	if(e[c][u].ch[s^1]) e[c][e[c][u].ch[s^1]].f = fa;
	e[c][fa].f = u;
	e[c][u].ch[s^1] = fa;
	push_up(fa,c);
}

inline void splay(int u,int c){
	push_down(u,c);
	while (!isrt(u,c)){
		if(isrt(e[c][u].f,c)) spin(u,c);
		else if(isr(u,c) ^ isr(e[c][u].f,c)) spin(u,c),spin(u,c);
		else spin(e[c][u].f,c),spin(u,c);
	}
	push_up(u,c);
}

inline void Access(int u,int c){
	for (int v = 0; u; u = e[c][v = u].f){
		splay(u,c);
		e[c][u].ch[1] = v;
		if (v) e[c][v].f = u;
		push_up(u,c);
	}
}

inline void Make_root(int u,int c){
	Access(u,c); splay(u,c);
	e[c][u].rev ^= 1;
}

inline bool Link(int u,int v,int c){
	if(Find(u,c) == Find(v,c)){
		printf("Error 2.\n");
		return false;
	}
	Make_root(u,c); Access(v,c); splay(v,c);
	e[c][u].f = v;
	return true;
}

inline void Cut(int u,int v,int c){
	Make_root(u,c); Access(v,c); splay(v,c);
	e[c][v].ch[0] = 0;
	e[c][u].f = 0;
	push_up(v,c);
}

inline void Change(int u,int w){
	for (int i = 0; i < C; i++){
		Access(u,i); splay(u,i);
		e[i][u].w = w;
		push_up(u,i);
	}
}

inline int Query(int u,int v,int c){
	if(Find(u,c) != Find(v,c)) return -1;
	Make_root(u,c); Access(v,c); splay(v,c);
	return e[c][v].Max;
}

void init(){
	for (int i = 0; i <= 10; i++) e[i][0].Max = -INF;
	N = read();
	M = read();
	C = read();
	K = read();
	int u,v,w;
	for (int i = 1; i <= N; i++){
		w = read();
		for (int j = 0; j < C; j++)
			e[j][i].w = e[j][i].Max = w;
	}
	while (M--){
		u = read();
		v = read();
		w = read();
		Link(u,v,w);
		edge[u][w][++edge[u][w][0]] = v;
		edge[v][w][++edge[v][w][0]] = u;
	}
}

void solve(){
	int k,x,y,z,c;
	while (K--){
		k = read();
		if (k == 0){
			x = read(); y = read();
			Change(x,y);
		}else if (k == 1){
			x = read(); y = read(); z = read();
			c = -1;
			for (int i = 0; i < C; i++)
				for (int j = 1; j <= edge[x][i][0]; j++)
					if (edge[x][i][j] == y){
						c = i;
						if (edge[x][i][0] == 2 && j == 1) swap(edge[x][i][1],edge[x][i][2]);
						if (edge[y][i][0] == 2 && edge[y][i][1] == x) swap(edge[y][i][1],edge[y][i][2]);
						break;
					}
			if (c == -1) printf("No such edge.\n");
			else if(c == z) printf("Success.\n");
			else if(edge[x][z][0] == 2 || edge[y][z][0] == 2) printf("Error 1.\n");
			else{
				if (Link(x,y,z)){
					edge[x][c][0]--;
					edge[y][c][0]--;
					edge[x][z][++edge[x][z][0]] = y;
					edge[y][z][++edge[y][z][0]] = x;
					Cut(x,y,c);
					printf("Success.\n");
				}
			}
		}else{
			c = read(); x = read(); y = read();
			printf("%d\n",Query(x,y,c));
		}
	}
}

int main()
{
	init();
	solve();
	return 0;
}