女神（goddess）——组合数学

出自某模拟赛。

题目大意：

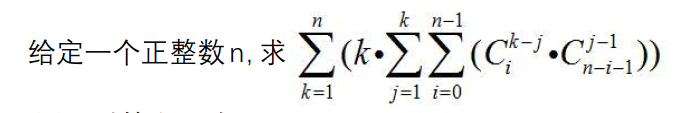
对1e9+7取模。

数据范围
 20 % ： n<=300
40 % ： n<=2,000
50 % ： n<=10,000
70 % ： n<=1,000,000
100 % ： n<=1,000,000,000

题解

方法众多。

然而我太蒟了，2h43min愣是写了一个40pts暴力走人。

开始指着想正解，但是发现想不出来，然后写n^2暴力，结果总是要么漏算要么算重要么取模出错。。。最后才调出来。

1.如果比较菜，请尝试打表：

$n^3$暴力显然。然后打表。

$n=1,ans_1=1$

$n=2,ans_2=6$

$n=3,ans_3=24$

$n=4,ans_4=80$

然后，套路的先观察相邻两项的关系。

然后尝试和项数的下标套上关系。

$ans_2=ans_1\times \frac{6}{1}$

$ans_3=ans_2\times \frac{8}{2}$

$ans_4=ans_3\times \frac{10}{3}$

诶，然后发现了规律！！

可以递推。

$f_{n+1}=f_n\times \frac{4+2\times n}{n}$

$f_{n+1}=f_n\times \frac{2\times(n+2)}{n}$

迭代下去得：

$f_{n+1}=f_1 \frac{2^n\times (n+2)!}{2n!}$

$f_{n+1}=\frac{2^{n}\times (n+1)\times(n+2)}{2}$

$f_{n}=\frac{2^{n-1}\times n\times(n+1)}{2}$

即可出结果

2.正解：

有点意思的是，i+n-i-1=n-1,k-j+j-1=k-1对于任意的i，j恒成立。

这就是突破口

考虑组合数的意义。

$\sum_{k=1}^n(k\times\sum_{j=1}^k\sum_{i=0}^{n-1}(C_i^{k-j}\times C_{n-i-1}^{j-1})$

$=\sum_{k=1}^n(k\times\sum_{i=0}^{n-1}\sum_{j=1}^k(C_i^{k-j}\times C_{n-i-1}^{j-1})$

j和i换了位置之后，

发现，其实i就是枚举的一个分割点，

然后对于选择的k-1个数，在1~i个数中选择k-j个，

在i+1~n-i-1个数中选择j-1个。

好像和$C_{n-1}^{k-1}$有些关系。

发现，对于$C_{n-1}^{k-1}$中的每个方案。

其实都可以找出0~n-1这n个分界点，然后统计一次。

每个方案被统计了n次。

所以，

原式

$=\sum_{k=1}^nk\times n\times C_{n-1}^{k-1}$

已经可以O(n)递推了。

我们可以用刚才的打表中方法，搞出递推式，然后迭代出来通项公式。

即可O(logn)求解。

3.但是这个还不够漂亮！！！

这个可是组合数啊！！不是一般的数。

组合数毕竟有实际的意义。

观察这个式子的组合意义。

$\sum_{k=1}^nk\times n\times C_{n-1}^{k-1}$

这个k-1和k，n有点麻烦。

提出来：

$=n\times (\sum_{k=1}^n(k-1)\times C_{n-1}^{k-1})+n\times 2^{n-1}$

第一个括号里面是什么意义？

对于n-1个数的集合中，所有子集的大小的和。

套路地，我们转化研究对象。

考虑每个元素被统计了几次。

就是：$2^{n-1-1}=2^{n-2}$

因为每个数自己必须出现一次，然后其他的数爱出现不出现。

所以，

$=n\times( n\times2^{n-2})+n\times 2^{n-1}$

然后就可以O(logn)计算了。

总结：

0.这个式子，我们尝试用数学知识、组合数公式化简，发现不容易化简。然后就要考虑组合数的意义。

1.组合数是一个有意义的数。这样的数学式子的推导，可以通过寻找式子的意义来进行化简。

往往起到立竿见影的效果。

2.打表找规律，要考虑把结果，递推关系和项的编号放在一起。