题目描述

http://codeforces.com/contest/1339/problem/A

给定一个 \(n(1\le n \le 10^9)\) ，问用一个由两个三角形组成的菱形，填充下面这种图形有多少种不同的填法。

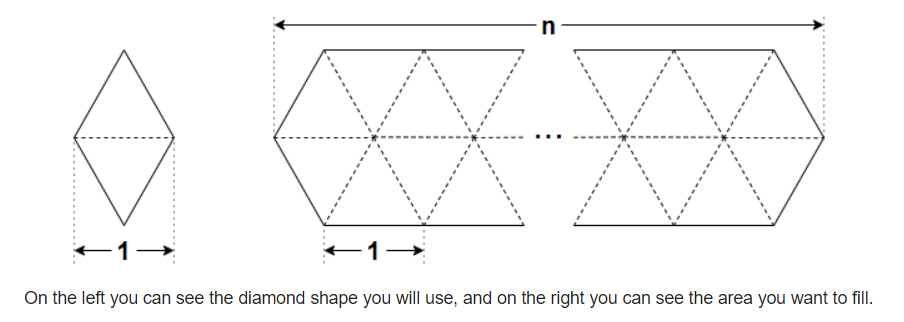
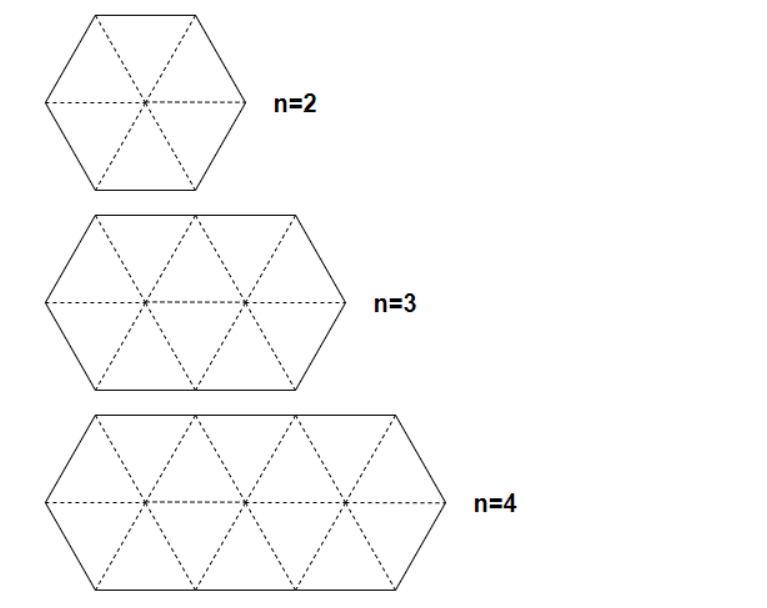
解题

通过枚举发现，被填充图形中竖着的菱形区域正好是 \(n\) 个。

而且在任何一种填充方式中，只能同时存在一个竖着的菱形填充，其余的填充必须是横向的菱形。

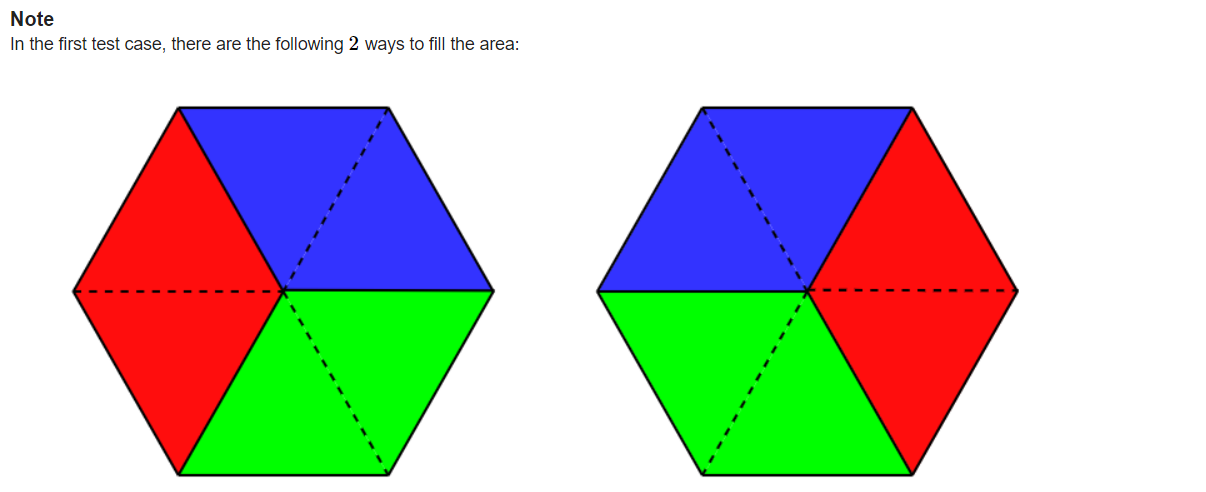
选取不同的竖向菱形区块填充，最终也都只能得到一种不同的填充方式。

所以填充方式数目 \(ans = n\) 。

for i in range(int(input())):

    print(input())

CF633(div.2)A. Filling Diamonds的更多相关文章

  1. Codeforces Round #566 (Div. 2) A. Filling Shapes

    链接: https://codeforces.com/contest/1182/problem/A 题意: You have a given integer n. Find the number of ...

  2. Codeforces Round #589 (Div. 2) B. Filling the Grid

    链接: https://codeforces.com/contest/1228/problem/B 题意: Suppose there is a h×w grid consisting of empt ...

  3. CF633(div.2)B. Sorted Adjacent Differences

    题目描述 http://codeforces.com/contest/1339/problem/B 有一个长度为 \(n(3\le n \le 10^5)\) 的整数序列 \(a_1,a_2,..., ...

  4. CF633(div.2)C. Powered Addition

    题目描述 http://codeforces.com/contest/1339/problem/C 给定一个长度为 \(n\) 的无序数组,你可以在第 \(x\) 秒进行一次下面的操作. 从数组选取任 ...

  5. Codeforces Round #589 (Div. 2) Another Filling the Grid (dp)

    题意:问有多少种组合方法让每一行每一列最小值都是1 思路:我们可以以行为转移的状态 附加一维限制还有多少列最小值大于1 这样我们就可以不重不漏的按照状态转移 但是复杂度确实不大行(减了两个常数卡过去的 ...

  6. Codeforces Round #633 (Div. 2)

    Codeforces Round #633(Div.2) \(A.Filling\ Diamonds\) 答案就是构成的六边形数量+1 //#pragma GCC optimize("O3& ...

  7. Codeforces Round #566 (Div. 2)

    Codeforces Round #566 (Div. 2) A Filling Shapes 给定一个 \(3\times n\) 的网格,问使用 这样的占三个格子图形填充满整个网格的方案数 如果 ...

  8. Codeforces Round #633 div2 A~C

    A. Filling Diamonds 题意:给你n个菱形方块,问能构成图示形状的有多少种 题解:自己画几个不难发现答案是n 代码: 1 #include <iostream> 2 #in ...

  9. Codeforces Round #589 (Div. 2)-E. Another Filling the Grid-容斥定理

    Codeforces Round #589 (Div. 2)-E. Another Filling the Grid-容斥定理 [Problem Description] 在\(n\times n\) ...

随机推荐

  1. h5 移动端适配方案思考

    基础概念 CSS像素(CSS pixels) 这个是浏览器使用的抽象单位,用来精确度量网页上的内容.平时经常写的width:100px;height:100px;都是与设备无关的. 设备独立像素(de ...

  2. C语言程序设计（八） 数组

    第八章 数组 //L8-1 #include <stdio.h> int main() { int score1, score2, score3, score4, score5; int ...

  3. wpf 菜单样式和绑定树形数据

    前言 在wpf开发中,经常会使用到Menu和ContentMenu.但是原生的样式比较简陋,对于比较追求界面美好的人来说是十分不友好的.那么,这就涉及到对Menu的样式修改了.与此同时,我们还希望Me ...

  4. angular 项目中遇到rxjs error TS1005:';'

    因为rxjs的版本问题,只需要在package.json 中将依赖的 rxjs:'^6.00' 改为 rxjs'6.00', 然后执行 npm update 更新下rxjs的依赖版本即可解决

  5. Mysql5.7及以上版本 ONLY_FULL_GROUP_BY报错

    近期在开发过程中,因为项目开发环境连接的mysql数据库是阿里云的数据库,而阿里云的数据库版本是5.6的.而测试环境的mysql是自己安装的5.7.因此在开发过程中有小伙伴不注意写了有关group b ...

  6. jdbc连接数据库三种方式

    ---恢复内容开始--- 第一种: public class Demo1 { //连接数据库的URL private String url = "jdbc:mysql://localhost ...

  7. 记一次RSA解密过程

    有问题可以评论 openssl rsa -pubin -text -modulus -in warmup -in pub.key

  8. c# Dictionary<string, object> 转JSON字符串

    JavaScriptSerializer jss = new JavaScriptSerializer(); Dictionary<string, object> dict = new D ...

  9. SVN分支合并指南

    SVN分支合并主干具体操作步骤 1. 在装有svn插件的myeclipse中,在主干上选择需要合并的文件或文件夹, 右击--> team -->合并(merge) 2.选择合并类型--合并 ...

  10. 【面试QA】Attention

    目录 Attention机制的原理 Attention机制的类别 双向注意力 Self-Attention 与 Soft-Attention 的区别 Transformer Multi-Head At ...