FFT快速傅里叶变换的python实现
FFT是DFT的高效算法,能够将时域信号转化到频域上,下面记录下一段用python实现的FFT代码。
# encoding=utf-8 import numpy as np
import pylab as pl # 导入和matplotlib同时安装的作图库pylab sampling_rate = 8000 # 采样频率8000Hz
fft_size = 512 # 采样点512,就是说以8000Hz的速度采512个点,我们获得的数据只有这512个点的对应时刻和此时的信号值。
t = np.linspace(0, 1, sampling_rate) # 截取一段时间,截取是任意的,这里取了0~1秒的一段时间。 x = np.sin(2*np.pi*156.25*t) + 2*np.sin(2*np.pi*234.375*t) # 输入信号序列,人工生成了一段信号序列,范围在0~1秒
xs = x[:fft_size] # 由上所述,我们只采样了512个点,所以我们只获得了前512个点的数据
xf = np.fft.rfft(xs)/fft_size # 调用np.fft的函数rfft(用于实值信号fft),产生长度为fft_size/2+1的一个复数向量,分别表示从0Hz~4000Hz的部分,这里之所以是4000Hz是因为Nyquist定理,采样频率8000Hz,则能恢复带宽为4000Hz的信号。最后/fft_size是为了正确显示波形能量 freqs = np.linspace(0, sampling_rate//2, fft_size//2 + 1) # 由上可知,我们得到了数据,现在产生0~4000Hz的频率向量,方便作图
xfp = 20*np.log10(np.clip(np.abs(xf), 1e-20, 1e1000)) # 防止幅值为0,先利用clip剪裁幅度,再化成分贝 pl.figure(figsize=(8, 4)) # 生成画布
pl.subplot(211) # 生成子图,211的意思是将画布分成两行一列,自己居上面。
pl.plot(t[:fft_size], xs) # 对真实波形绘图
pl.xlabel(u"time(s)")
pl.title(u"The Wave and Spectrum of 156.25Hz and 234.375Hz")
pl.subplot(212) # 同理
pl.plot(freqs, xfp) # 对频率和幅值作图,xlabel是频率Hz,ylabel是dB
pl.xlabel(u"Hz")
pl.subplots_adjust(hspace=0.4) # 调节绘图参数
pl.show()
代码进行了详细标注。有一个小细节是FFT对于取样时间有要求。N点FFT进行精确频谱分析的要求是N个取样点包含整数个取样对象的波形。因此N点FFT能够完美计算频谱,对取样对象的要求是n*Fs/N(n*采样频率/FFT长度)在本例中Fs = 8000Hz,N=512 base_freq=15.625Hz 所以本例中给出了频率为156.25Hz(n=10)和234.375Hz(n=15)做例子。
效果如下: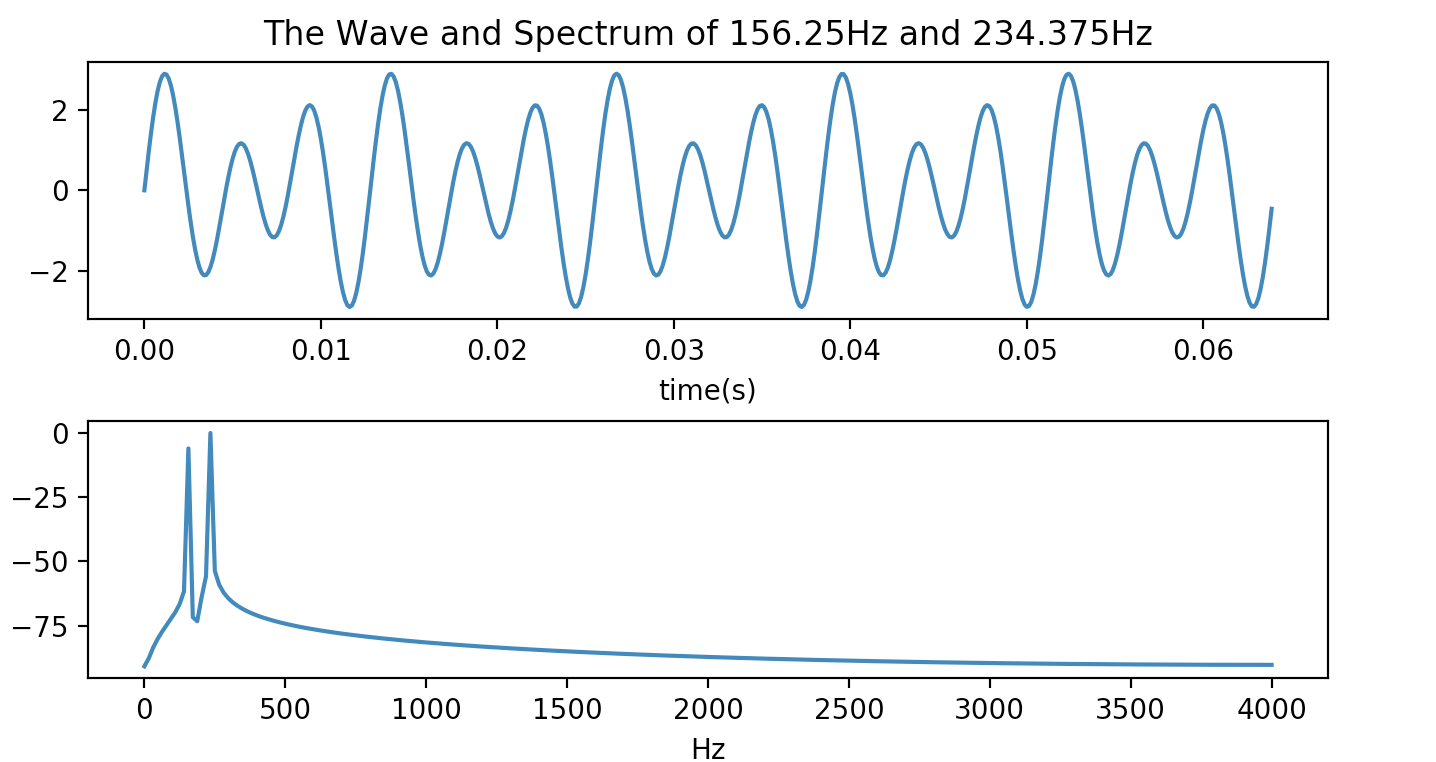
FFT快速傅里叶变换的python实现的更多相关文章
- CQOI2018 九连环 打表找规律 fft快速傅里叶变换
题面: CQOI2018九连环 分析: 个人认为这道题没有什么价值,纯粹是为了考算法而考算法. 对于小数据我们可以直接爆搜打表,打表出来我们可以观察规律. f[1~10]: 1 2 5 10 21 4 ...
- FFT 快速傅里叶变换 学习笔记
FFT 快速傅里叶变换 前言 lmc,ikka,attack等众多大佬都没教会的我终于要自己填坑了. 又是机房里最后一个学fft的人 早背过圆周率50位填坑了 用处 多项式乘法 卷积 \(g(x)=a ...
- 「学习笔记」FFT 快速傅里叶变换
目录 「学习笔记」FFT 快速傅里叶变换 啥是 FFT 呀?它可以干什么? 必备芝士 点值表示 复数 傅立叶正变换 傅里叶逆变换 FFT 的代码实现 还会有的 NTT 和三模数 NTT... 「学习笔 ...
- FFT快速傅里叶变换算法
1.FFT算法概要: FFT(Fast Fourier Transformation)是离散傅氏变换(DFT)的快速算法.即为快速傅氏变换.它是根据离散傅氏变换的奇.偶.虚.实等特性,对离散傅立叶变换 ...
- 傅里叶变换通俗解释及快速傅里叶变换的python实现
通俗理解傅里叶变换,先看这篇文章傅里叶变换的通俗理解! 接下来便是使用python进行傅里叶FFT-频谱分析: 一.一些关键概念的引入 1.离散傅里叶变换(DFT) 离散傅里叶变换(discrete ...
- FFT —— 快速傅里叶变换
问题: 已知A[], B[], 求C[],使: 定义C是A,B的卷积,例如多项式乘法等. 朴素做法是按照定义枚举i和j,但这样时间复杂度是O(n2). 能不能使时间复杂度降下来呢? 点值表示法: 我们 ...
- [C++] 频谱图中 FFT快速傅里叶变换C++实现
在项目中,需要画波形频谱图,因此进行查找,不是很懂相关知识,下列代码主要是针对这篇文章. http://blog.csdn.net/xcgspring/article/details/4749075 ...
- matlab中fft快速傅里叶变换
视频来源:https://www.bilibili.com/video/av51932171?t=628. 博文来源:https://ww2.mathworks.cn/help/matlab/ref/ ...
- FFT快速傅里叶变换
FFT太玄幻了,不过我要先膜拜HQM,实在太强了 1.多项式 1)多项式的定义 在数学中,由若干个单项式相加组成的代数式叫做多项式.多项式中的每个单项式叫做多项式的项,这些单项式中的最高项次数,就是这 ...
随机推荐
- Flask搭建个人博客网站(1)—项目规划--李渣渣(lizaza.cn)
Flask搭建个人博客网站(1)—项目规划--李渣渣(lizaza.cn) 发布时间:2020-05-2413次浏览 前言 现在市面上又许多比较成熟的博客平台,例如:CSDN,博客园,新浪博客等!对于 ...
- JAVA ArrayList集合基础
java集合的使用方法 一,集合ArrayList的定义方式 ArrayLsit<数据类型> 变量名=new ArrayList<数据类型>(); 二,集合的操作和概念 ...
- [ES6系列-04]再也不乱“哇”了:用 let 与 const 替代 var
[原创]码路工人 Coder-Power 大家好,这里是码路工人有力量,我是码路工人,你们是力量. github-pages 博客园cnblogs 今天的内容是,关于 JavaScript 中定义变量 ...
- 读Pyqt4教程,带你入门Pyqt4 _013
你是否曾经看着应用程序并思考特定的GUI项是如何产生的?大概每位程序员都这样过.然后你能看到你喜欢的GUI库提供的一系列窗口组件,但是你无法找到它.工具包通常仅仅提供最常用的窗口组件,比如按钮.文本组 ...
- Postgre数据库自定义函数
自定函数 1.查询函数: select prosrc from pg_proc where proname='test' 参数说明 : test 为函数名. 2.删除函数: drop function ...
- SpringBoot—自定义线程池及并发定时任务模板
介绍 在项目开发中,经常遇到定时任务,今天通过自定义多线程池总结一下SpringBoot默认实现的定时任务机制. 定时任务模板 pom依赖 <dependencies> <dep ...
- Java IO(五)字节流 FileInputStream 和 FileOutputStream
Java IO(五)字节流 FileInputStream 和 FileOutputStream 一.介绍 字节流 InputStream 和 OutputStream 是字节输入流和字节输出流的超类 ...
- SSIS 数据类型 第二篇:变量的数据类型
变量(Variable)用于存储在Package运行时用到的值,集成服务支持两种类型的变量:用户自定义的变量和系统变量,自定义的变量由用户来定义,系统变量由集成服务来定义. 变量的用途十分广泛,用于容 ...
- 05 . 前端之BootStrap
BootStrap简介 Bootstrap是美国Twitter公司的设计师Mark Otto和Jacob Thornton合作基于HTML.CSS.JavaScript 开发的简洁.直观.强悍的前端开 ...
- Java实现蓝桥杯 九宫幻方
九宫幻方 D: 今天做一道题目 九宫幻方 小明最近在教邻居家的小朋友小学奥数,而最近正好讲述到了三阶幻方这个部分. 三阶幻方指的是将1~9不重复的填入一个3*3的矩阵当中,使得每一行.每一列和每一条对 ...
