字符串匹配算法 之BF、KMP

示例：

1. 已知字符串str1="acabaabaabcacaabc",求str2="abaabcac"是否在字符串str1中？

2. DNA病毒检测。已知患者DNA序列求病毒DNA序列是否在患者DNA中出现过？病毒DNA为环状结构（即首尾相连）。

此文以问题1为例进行解答。

一、BF算法：

即暴力检测法，从字符串第一个字符开始和匹配字符串进行比较如果不同，则从字符串第二个位置开始比较直到结束。

BF算法思想很简单，直接列出代码实现：

 static void Main(string[] args)
        {
            string str = "acabaabaabcacaabc";//"aaabaaaaaab";
            string mo = "abaabc";//"aaaab";int flag;//表示查询结果
            flag = BF(str, mo, );
            if (flag != -) Console.WriteLine("匹配成功！" + "  下标为: " + flag);
            else Console.WriteLine("匹配失败！");
        }

 private static int BF(string str, string mo, int v)
        {
            int i = v ,j = ;
            while (i < str.Length && j < mo.Length)
            {
                if (str[i] == mo[j])
                {
                    i++;
                    j++;
                }
                else
                {
                    i = i - j + ;
                    j = ;
                }
            }
            if (j >= mo.Length) return i - mo.Length;
            else return -;
        }

二、KMP算法：

如图：

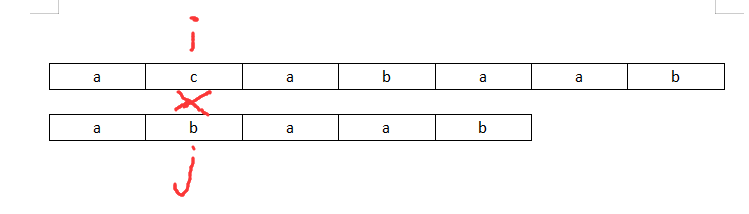
在检测中发现i和j标记的元素不同，此时如果是BF算法直接ii= i-j+1,j = 0.但是KMP算法思想是让i下标不变，j下标变化，即可以理解为数组str2右移尽可能少的单位。

问题来了，如何知道要移动多少呢?

如图，我们可以知道，在数组str2中j下标之前的所有元素都和数组str1的对应位匹配，那么我们只要保证，将str2数组向右移动k，使得在str2中j=k元素之前的元素依旧匹配即可。因此引入

前缀和后缀的概念，前缀：元素的真子集 ，后缀：元素的反向真子集。即如aba三个元素，最长前缀为ab,最长后缀为ba。但是只有前缀a和后缀a相同所以str2的第四个元素的

next值为1；也就是当匹配到str[3]不同于str1时，此时j下标变为1即str2向右移动到j==下标1。

为此我们只需要根据str2得到next数组就行。即得到str2的最大匹配前后缀个数。默认a[0]=0;即变化值为next值-1.因为next值是在字符串下标从1开始，我们开发通常下标从0开始

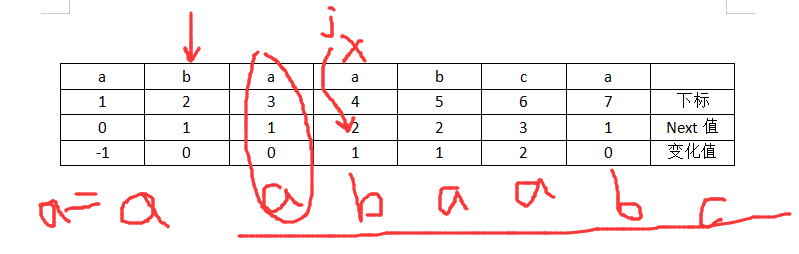
代码如下：

 static void Main(string[] args)
        {
            string str = "acabaabaabcacaabc";//"aaabaaaaaab";
            string mo = "abaabc";//"aaaab";
            int[] next=new int[mo.Length];
            int flag;//表示查询结果
            setNext(mo, next);
            foreach (var item in next)
            {
                Console.Write(item + " ");
            }
            Console.WriteLine();
            flag = KMP(str, mo, , next);
            if (flag != -) Console.WriteLine("匹配成功！" + "  下标为: " + flag);
            else Console.WriteLine("匹配失败！");
        }

  private static void setNext(string mo, int[] next)
        {
            int i = , j = -;
            next[] = -;
            while (i < mo.Length - )
            {
                if (j == - || mo[i] == mo[j])
                {
                    i++; j++;
                    next[i] = j;
                }
                else j = next[j];
            }
        }

   private static int KMP(string str, string mo, int v,int[] next)
        {
            int i = v, j = ;
            while (i < str.Length && j < mo.Length)
            {
                if (j==- || str[i] == mo[j])
                {
                    i++;
                    j++;
                }
                else
                {
                    j = next[j];
                }
            }
            if (j >= mo.Length) return i - mo.Length;
            else return -;
        }

//进一步对next数组优化
private static void setNextVal(string mo, int[] next)
        {
            int i = , j = -;
            next[] = -;
            while (i < mo.Length-)
            {
                if (j == - || mo[i] == mo[j])
                {
                    i++; j++;
                    if (mo[i] != mo[j]) next[i] = j;
                    else next[i] = next[j];
                }
                else j = next[j];
            }
        }