聚类（三）FUZZY C-MEANS 模糊c-均值聚类算法——本质和逻辑回归类似啊

摘自：http://ramsey16.net/%E8%81%9A%E7%B1%BB%EF%BC%88%E4%B8%89%EF%BC%89fuzzy-c-means/

经典k-均值聚类算法的每一步迭代中，每一个样本点都被认为是完全属于某一类别。我们可以放松这个条件，假定每个样本xjxj模糊“隶属”于某一类的。

硬聚类把每个待识别的对象严格的划分某类中，具有非此即彼的性质；模糊聚类建立了样本对类别的不确定描述，更能客观的反应客观世界，从而成为聚类分析的主流。

例1、一个一维的例子来说，给定一个特定数据集，分布如下图：

图中可以很容易分辨出两类数据，分别表示为‘A’ and ‘B’. 利用前述的k-means 算法，每个数据关联一个特定的质心，隶属度函数如下所示：

用FCM 算法，同一个数据并不单独属于一个分类，而是可以出现在中间。在这个例子中，隶属函数变得更加平滑，表明每个数据可能属于几个分类。

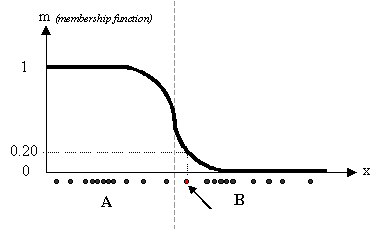
上图中，红色点表示的数据更可能属于类别B，而不是A， ‘m’ 的值0.2表明了数据对A的隶属程度。