Exclusive or

题目连接

• 题意：
  
  每次给一个n。求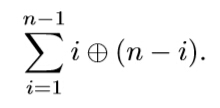
  
  (2≤n<10⁵⁰⁰)
• 分析：
  
  先说一下自己的想法，假设将n换成二进制数，也就一两千位左右，那么一位一位处理是能够接受的。

  将0-n写成二进制形式后，显然全部数某一个二进制位是有一个循环节的。那么我们就能够从这里入手直接求解

import java.io.*;
import java.math.*;
import java.util.*;

public class Main {
    public static BigInteger zero = BigInteger.ZERO;
    public static BigInteger one = BigInteger.ONE;
    public static BigInteger two = BigInteger.valueOf(2);
    public static BigInteger three = BigInteger.valueOf(3);
    public static BigInteger four = BigInteger.valueOf(4);
    public static BigInteger six = BigInteger.valueOf(6);

    public static BigInteger Down(BigInteger now, BigInteger L) {
    	BigInteger mid = now.divide(L).multiply(L).add(L.shiftRight(1));
    	if (now.subtract(mid).signum() < 0)
    		return mid;
    	return mid.add(L.shiftRight(1));
    }

    public static BigInteger Up(BigInteger now, BigInteger L) {
    	BigInteger start = now.divide(L).multiply(L);
    	BigInteger mid = start.add(L.shiftRight(1));
    	if (now.subtract(mid).signum() < 0)
    		return start.subtract(one);
    	return mid.subtract(one);
    }

    public static int getValue(BigInteger now, BigInteger L) {
    	BigInteger mid = now.divide(L).multiply(L).add(L.shiftRight(1));
    	if (now.subtract(mid).signum() < 0)
    		return 0;
    	return 1;
    }

    public static BigInteger solve(BigInteger nl, BigInteger nr, BigInteger gl, BigInteger L) {
    	BigInteger ret = zero, step = Down(nl, L).subtract(nl), t = nr.subtract(Up(nr, L));
    	if (step.subtract(t).signum() > 0)
    		step = t;
    	while (nl.add(step).subtract(gl).signum() <= 0) {
    		if ((getValue(nl, L) ^ getValue(nr, L)) == 1)
    			ret = ret.add(step);
    		nl = nl.add(step); nr = nr.subtract(step);
    		step = Down(nl, L).subtract(nl); t = nr.subtract(Up(nr, L));
    		if (step.subtract(t).signum() > 0)
        		step = t;
    	}
    	if (gl.subtract(nl).add(one).signum() >= 0 && (getValue(nl, L) ^ getValue(nr, L)) == 1)
    		ret = ret.add(gl.subtract(nl).add(one));
    	return ret;
    }

    public static void main(String[] args) {
    	BigInteger n, L, tans, nl, ans;
    	Scanner cin = new Scanner(System.in);
    	while (cin.hasNext()) {
    		n = cin.nextBigInteger();
    		L = two;
    		ans = zero;
    		while (L.subtract(n.shiftLeft(1)).signum() <= 0)//(L <= n * 2)
    		{
    			tans = zero;
    			if (n.divide(L).shiftRight(1).signum() > 0) {
	    			tans = solve(zero, n, L.subtract(one), L);
	    		}
    			nl = n.divide(L).shiftRight(1).multiply(L);
    			tans = n.divide(L).shiftRight(1).multiply(tans).add(solve(nl, n.subtract(nl), n.subtract(one).shiftRight(1), L));
    			ans = ans.add(tans.multiply(L));
    			L = L.shiftLeft(1);
    		}
    		System.out.println(ans.subtract(n.shiftLeft(1)));
    	}
    }
}

学习一下题解的方法。关键在于：(2 * k) ^ x = (2 * k + 1) ^ x

之后就学习一下题解的公式化简方法了

import java.util.*;
import java.math.*;

public class Main {
	static BigInteger n, ret;
	static BigInteger one = BigInteger.valueOf(1);
	static BigInteger two = BigInteger.valueOf(2);
	static BigInteger four = BigInteger.valueOf(4);
	static BigInteger six = BigInteger.valueOf(6);
	static HashMap<BigInteger, BigInteger> mp = new HashMap<BigInteger, BigInteger>();
	public static BigInteger fun(BigInteger n) {
		if (n.equals(BigInteger.ZERO) || n.equals(BigInteger.ONE))
			return BigInteger.ZERO;
		if (mp.containsKey(n))
			return mp.get(n);
		BigInteger k = n.shiftRight(1);
		if (n.testBit(0)) {
			ret = four.multiply(fun(k)).add(six.multiply(k));
			mp.put(n, ret);
			return ret;
		}
		else {
			ret = (fun(k).add(fun(k.subtract(one))).add(k.shiftLeft(1)).subtract(two)).shiftLeft(1);
			mp.put(n, ret);
			return ret;
		}
	}
	public static void main(String[] args) {
		Scanner cin = new Scanner(System.in);
		while (cin.hasNext()) {
			n = cin.nextBigInteger();
			mp.clear();
			System.out.println(fun(n));
		}
	}
}