Surround the Trees HDU 1392 凸包

Problem Description

There are a lot of trees in an area. A peasant wants to buy a rope to surround all these trees. So at first he must know the minimal required length of the rope. However, he does not know how to calculate it. Can you help him? 
The diameter and length of the trees are omitted, which means a tree can be seen as a point. The thickness of the rope is also omitted which means a rope can be seen as a line.

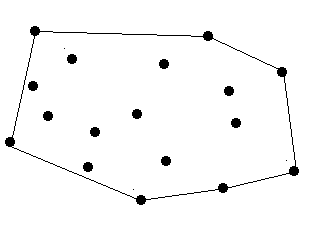
There are no more than 100 trees.

 

Input

The input contains one or more data sets. At first line of each input data set is number of trees in this data set, it is followed by series of coordinates of the trees. Each coordinate is a positive integer pair, and each integer is less than 32767. Each pair is separated by blank.

Zero at line for number of trees terminates the input for your program.

 

Output

The minimal length of the rope. The precision should be 10^-2.

 

Sample Input

9
12 7
24 9
30 5
41 9
80 7
50 87
22 9
45 1
50 7
0

 

Sample Output

243.06

 

Source

Asia 1997, Shanghai (Mainland China)

 

Recommend

Ignatius.L   |   We have carefully selected several similar problems for you:  2150 1348 1147 1558 1374 

 

计算几何比较大小 判断正负 千万要用 sgn函数！ 精度！精度！

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<sstream>
#include<algorithm>
#include<queue>
#include<deque>
#include<iomanip>
#include<vector>
#include<cmath>
#include<map>
#include<stack>
#include<set>
#include<fstream>
#include<memory>
#include<list>
#include<string>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
#define MAXN 109
#define N 21
#define MOD 1000000
#define INF 1000000009
const double eps = 1e-;
const double PI = acos(-1.0);
/*
所有线段投射到给定线段上取交集，如果交集距离大于eps 存在！ｓ
*/
int sgn(double x)
{
    if (fabs(x) < eps) return ;
    if (x < ) return -;
    else return ;
}
struct Point
{
    double x, y;
    Point() {}
    Point(double _x, double _y) :x(_x), y(_y) {}
    Point operator - (const Point& r)const
    {
        return Point(x - r.x, y - r.y);
    }
    double operator ^(const Point& r)const
    {
        return x*r.y - y*r.x;
    }
    double operator * (const Point& r)const
    {
        return x*r.x + y*r.y;
    }
};
double dist(Point a, Point b)
{
    return sqrt((a - b)*(a - b));
}
struct Line
{
    Point s, e;
    Line() {}
    Line(Point _a, Point _B) :s(_a), e(_B) {}
};
bool Seg_inter_line(Line l1, Line l2)
{
    return sgn((l2.s - l1.e) ^ (l1.s - l1.e))*sgn((l2.e - l1.e) ^ (l1.s - l1.e)) <= ;
}
bool cross(Line l1, Line l2)
{
    return
        max(l1.s.x, l1.e.x) >= min(l2.s.x, l2.e.x) &&
        max(l2.s.x, l2.e.x) >= min(l1.s.x, l1.e.x) &&
        max(l1.s.y, l1.e.y) >= min(l2.s.y, l2.e.y) &&
        max(l2.s.y, l2.e.y) >= min(l1.s.y, l1.e.y) &&
        sgn((l2.s - l1.e) ^ (l1.s - l1.e))*sgn((l2.e - l1.e) ^ (l1.s - l1.e)) <=  &&
        sgn((l1.s - l2.e) ^ (l2.s - l2.e))*sgn((l1.e - l2.e) ^ (l2.s - l2.e)) <= ;
}
double CalcArea(Point p[], int n)
{
    double res = ;
    for (int i = ; i < n; i++)
        res += (p[i] ^ p[(i + ) % n]) / ;
    return fabs(res);
}
double CalcLen(Point p[],int n)
{
    double res = ;
    for (int i = ; i < n; i++)
        res += dist(p[i], p[(i + ) % n]);
    return (res);
}
bool isconvex(Point p[], int n)
{
    bool s[];
    memset(s, false, sizeof(s));
    for (int i = ; i < n; i++)
    {
        s[sgn((p[(i + ) % n] - p[i]) ^ (p[(i + ) % n] - p[i])) + ] = true;
        if (s[] && s[])
            return false;
    }
    return true;
}
//Point Calgravitycenter(Point p[], int n)
//{
//    Point res(0, 0);
//    double area = 0;
//    for (int i = 0; i < n; i++)
//    {
//        ci[i] = (p[i] ^ p[(i + 1) % n]);
//        ti[i].x = (p[i].x + p[(i + 1) % n].x);
//        ti[i].y = (p[i].y + p[(i + 1) % n].y);
//        res.x += ti[i].x * ci[i];
//        res.y += ti[i].y * ci[i];
//        area += ci[i] / 2;
//    }
//    res.x /= (6 * area);
//    res.y /= (6 * area);
//    return res;
//}
Point L[MAXN],tmp[MAXN];
int Stack[MAXN], top;
bool cmp(Point p1, Point p2)
{
    double tmp = (p1 - L[]) ^ (p2 - L[]);
    if (sgn(tmp) > )
        return true;
    else if (sgn(tmp) ==  && sgn(dist(p1, L[]) - dist(p2, L[]) <= ))
        return true;
    else
        return false;
}
double Graham(int n)
{
    Point p0;
    int k = ;
    p0 = L[];
    for (int i = ; i < n; i++)
    {
        if ((p0.y > L[i].y) || (p0.x == L[i].x&&p0.x > L[i].x) )
        {
            k = i, p0 = L[i];
        }
    }
    swap(L[k], L[]);
    sort(L + , L + n, cmp);
    if (n == )
    {
        top = , Stack[] = ;
        return 0.0;
    }
    else if (n == )
    {
        top = , Stack[] = , Stack[] = ;
        return dist(L[],L[]);
    }
    Stack[] = , Stack[] = , top = ;
    for (int i = ; i < n; i++)
    {
        while (top >  && sgn((L[Stack[top - ]] - L[Stack[top - ]]) ^ (L[i] - L[Stack[top - ]])) <= )
        {
            top--;
        }
        Stack[top++] = i;
    }
    double res = ;
    for (int i = ; i < top; i++)
        res += dist(L[Stack[i]], L[Stack[(i + ) % top]]);
    return res;
}
int main()
{
    int n;
    while (scanf("%d", &n), n)
    {
        for (int i = ; i < n; i++)
            scanf("%lf%lf", &L[i].x, &L[i].y);
        printf("%.2lf\n", Graham(n));
    }
}