OpenGL（一）绘制圆、五角星、正弦曲线

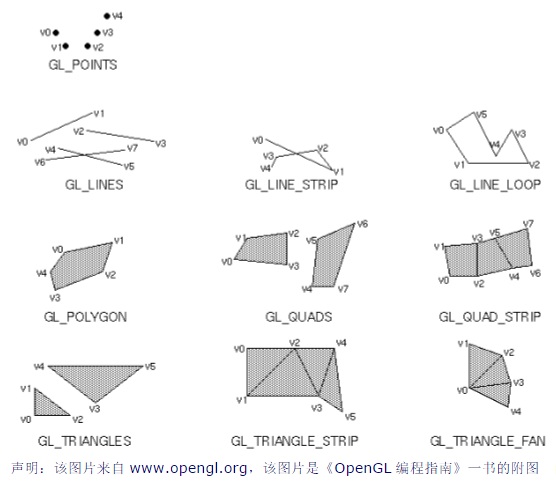
OpenGL入门之“顶点”：OpenGL规定，一个多边形必须是一个“凸多边形”，即连接多边形上任意两点，其连线都在多边形内部。多边形可以由其边上的端点（这里可称为顶点）来确定。所以“顶点”的概念在图形学中非常重要，定义了顶点数组和顶点的连接方式，就可以组合出各种形态。

OpenGL中顶点连接形式：顶点的连接形式由glBegin函数定义，每种参数对应的连接形式如下：

对OpenGL绘图的初步实践，分别绘制圆、五角星和正弦曲线。

#include <glut.h>
#include "math.h"
#include <iostream>

using namespace std;

int n=3600;  //圆绘制次数
float PI=3.1415926f;
float R=0.8f;  //半径

void myDisplay(void)
{
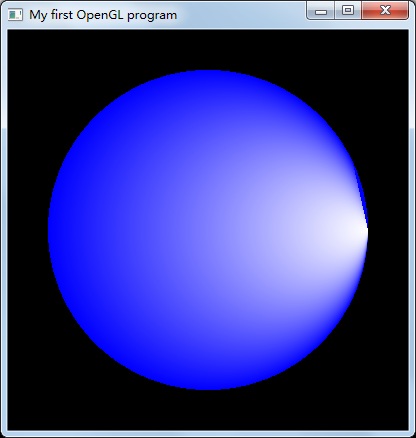
	//画圆
	glClear(GL_COLOR_BUFFER_BIT);
	glClearColor(0,0,0,0);
	glColor4f(0,0,1,0);
	glBegin(GL_POLYGON);
	for(int i=0;i<n;i++)
	{
		glVertex2f(R*cos(2*PI*i/n),R*sin(2*PI*i/n));   //定义顶点
	}
	glEnd();
	glFlush();

	cout<<"画圆成功，任意键继续…"<<endl;
	system("pause");

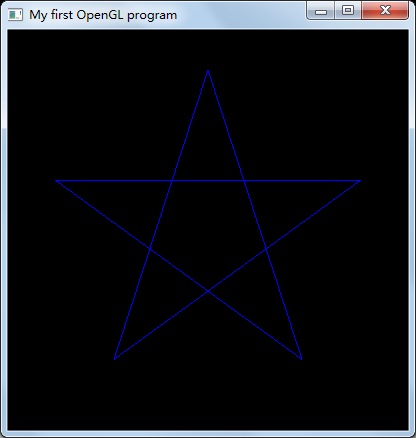
	//画五角星
	glClear(GL_COLOR_BUFFER_BIT);
	glClearColor(0,0,0,0);
	glColor4f(0,0,1,0);
	glBegin(GL_LINE_LOOP);

	//以下ABCDE分别是五角星的5个顶点
	GLfloat xA=R*cos(90*2*PI/360);
	GLfloat yA=R*sin(90*2*PI/360);

	GLfloat xB=R*cos(306*2*PI/360);
	GLfloat yB=R*sin(306*2*PI/360);

	GLfloat xC=R*cos(162*2*PI/360);
	GLfloat yC=R*sin(162*2*PI/360);

	GLfloat xD=R*cos(18*2*PI/360);
	GLfloat yD=R*sin(18*2*PI/360);

	GLfloat xE=R*cos(234*2*PI/360);
	GLfloat yE=R*sin(234*2*PI/360);

	glVertex2f(xA,yA);
	glVertex2f(xB,yB);
	glVertex2f(xC,yC);
	glVertex2f(xD,yD);
	glVertex2f(xE,yE);
	glEnd();
	glFlush();

	cout<<"画五角星成功，任意键继续…"<<endl;
	system("pause");

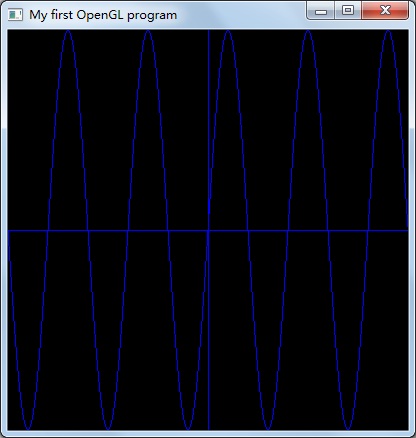
	//画正弦曲线，画5个，在x方向上压缩
	GLfloat x=-1.0;
	glClear(GL_COLOR_BUFFER_BIT);
	glBegin(GL_LINES);

	glVertex2f(-1.0f,0.0f);  //过中心的十字
	glVertex2f(1.0f,0.0f);
	glVertex2f(0.0f,-1.0f);
	glVertex2f(0.0f,1.0f);

	glEnd();
	glBegin(GL_LINE_STRIP);
	for(float x=-5*PI;x<5*PI;x+=0.1f)
	{
		glVertex2f(x/(5*PI),sin(x));
	}
	glEnd();
	glFlush();
	cout<<"正弦线完成"<<endl;
}  

int main(int argc, char *argv[])
{
	glutInit(&argc, argv);   //初始化GLUT
	glutInitDisplayMode(GLUT_RGB | GLUT_SINGLE);
	glutInitWindowPosition(100, 100);
	glutInitWindowSize(400, 400);
	glutCreateWindow("My first OpenGL program");
	glutDisplayFunc(&myDisplay);   //回调函数
	glutMainLoop();    //持续显示，当窗口改变会重新绘制图形
	return 0;
}  

圆：

五角星：

正弦曲线：

1. OpenGL中窗口的坐标是笛卡尔坐标系，原点在窗口的中心点，左右和上下边界坐标分别为-1、1、1、-1。水平方向上是x轴，垂直方向上是y轴。

2. 图像窗口每次改变，都会引发重绘。

3. 绘制这些简单图形的核心是顶点坐标的确定，依序分别绘制，顺序很重要。