Python的主成分分析PCA算法

这篇文章很不错：https://blog.csdn.net/u013082989/article/details/53792010

为什么数据处理之前要进行归一化？？？（这个一直不明白）

这个也很不错：https://blog.csdn.net/u013082989/article/details/53792010#commentsedit

下面是复现一个例子：

# -*- coding: utf-8 -*-

#来源：https://blog.csdn.net/u013082989/article/details/53792010
#来源：https://blog.csdn.net/hustqb/article/details/78394058  （这里有个例子）关于降维之后的坐标系问题，？？？结合里面的例子

#用库函数实现的过程：

#导入需要的包：
import numpy as np
from matplotlib import pyplot as plt
from scipy import io as spio
from sklearn.decomposition import pca
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt

#归一化数据,并作图
def scaler(X):
    """
    注：这里的归一化是按照列进行的。也就是把每个特征都标准化，就是去除了单位的影响。
    """
    scaler=StandardScaler()
    scaler.fit(X)
    x_train=scaler.transform(X)
    return x_train

#使用pca模型拟合数据并降维n_components对应要降的维度
def jiangwei_pca(x_train,K):                       #传入的是X的矩阵和主成分的个数K
    model=pca.PCA(n_components=K).fit(x_train)
    Z=model.transform(x_train)                     #transform就会执行降维操作

#数据恢复，model.components_会得到降维使用的U矩阵

Ureduce=model.components_
    x_rec=np.dot(Z,Ureduce)                       #数据恢复

return Z,x_rec                                #这里Z是将为之后的数据，x_rec是恢复之后的数据。

if __name__ == '__main__':
    X=np.array([[1,1],[1,3],[2,3],[4,4],[2,4]])
    x_train=scaler(X)
    print('x_train:',x_train)
    Z,x_rec=jiangwei_pca(x_train,2)
    print("Z:",Z)
    print("x_rec:",x_rec)                          #如果有时候，这里不能够重新恢复x_train，一个原因可能是主成分太少。
    print("x_train:",x_train)

##    这里的主成分为什么不是原来的两个。

##   还有一个问题是，如何用图像表现出来。

##   还有一个问题就是如何得到系数，这个系数是每个特征在主成分中的贡献，要做这个就需要看矩阵，弄明白原理：

或许和这个程序有关：pca.explained_variance_ratio_

摘自：https://blog.csdn.net/qq_36523839/article/details/82558636

这里提一点：pca的方法explained_variance_ratio_计算了每个特征方差贡献率，所有总和为1，explained_variance_为方差值，通过合理使用这两个参数可以画出方差贡献率图或者方差值图，便于观察PCA降维最佳值。

在提醒一点：pca中的参数选项可以对数据做SVD与归一化处理很方便，但是需要先考虑是否需要这样做。

关于pca的一个推导例子：

、、

根据最后的图形显示来看，一共有五个样本点。而从下面的矩阵看，似乎不是这样？？？

有点纠结。

从对矩阵X的求均值过程可以知道，是对行求均值的。然后每行减掉均值。

（这样的话，也就是说：每一行是一个特征？？？，就不太明白了。）

应该写成这样比较清楚：（每一列是一个特性）

[

[1,1]

[1,3]

[2,3]

[4,4]

[2,4]

]

、、

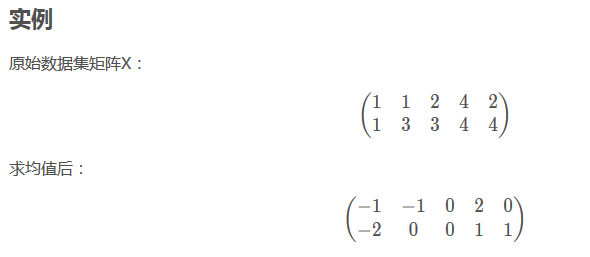
从下面看出这里除的是5，也就是说5是m，也就是行数。？？？

、、

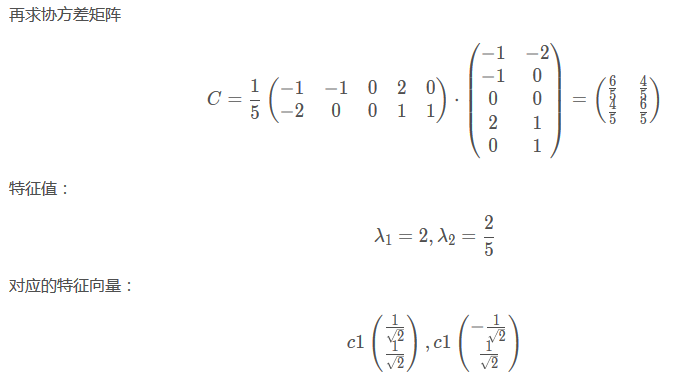
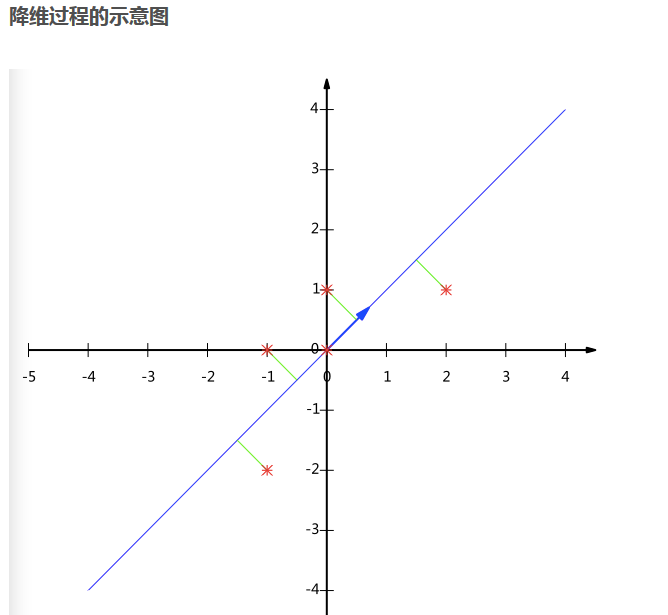
最后降维到一个特征：：

下面图片中P的部分，是两个数，也就是两个特征的系数。代表着特征的系数。。。

关键是用的别人的库，但是怎么弄？？？

、、

上面

#、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、

下面我们来分析另一个例子：这个例子是官方给出的：

程序如下：

# -*- coding: utf-8 -*-

"""
测试

这里是Python的pca主成分分析的一个测试程序
"""
import numpy as np
from sklearn.decomposition import PCA

X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
pca = PCA(n_components='mle')                                                  #这里是让机器决定主成分的个数，我们也可以自行设置。
pca = PCA(n_components=2)                                                      #这里设置主成分为，这里不能设置成3，因为这里的特征本身只有两个。
pca.fit(X)

print("这里是X:")
print(X)

Z=pca.transform(X)                                                             #transform就会执行降维操作
print('这里是Z：')
print(Z)

# Z = np.dot(X, self.components_.T)

# PCA(copy=True, n_components=2, whiten=False)
print(pca.explained_variance_ratio_)

然后运行程序输出的结果：

这里是X:
[[-1 -1]
 [-2 -1]
 [-3 -2]
 [ 1  1]
 [ 2  1]
 [ 3  2]]
可能是系数的东西：  这里有可能是没个主成分中包含各个特征的权重系数。

你有没有感觉到这个矩阵有一定的特性，有点对角线对称的样子。
[[-0.83849224  0.54491354]
 [-0.54491354 -0.83849224]]
这里是Z：                 这里的Z实际上主成分的意思。主成分也就是综合特征
[[ 1.38340578   0.2935787 ]
 [ 2.22189802  -0.25133484]
 [ 3.6053038    0.04224385]
 [-1.38340578  -0.2935787 ]
 [-2.22189802   0.25133484]
 [-3.6053038   -0.04224385]]

[0.99244289 0.00755711]

要捋清一个问题，我们想要得到的是什么？

我们想要得到的是每个主成分前面包含特征的系数。

主成分1=权重11*特征1+权重12*特征2+权重13*特征3···

主成分2=权重21*特征1+权重22*特征2+权重23*特征3···

[[-0.83849224  0.54491354]
 [-0.54491354 -0.83849224]]

主成分1=（-0.83849224） *特征1+（-0.54491354）*特征2···

主成分2=（0.54491354）  *特征1+（-0.83849224）*特征2···

就是上面这种系数，

我还是有一点疑问？为什么？这个系数矩阵是对称的，这样有点不是很科学？？