（数据科学学习手札13）K-medoids聚类算法原理简介&Python与R的实现

前几篇我们较为详细地介绍了K-means聚类法的实现方法和具体实战，这种方法虽然快速高效，是大规模数据聚类分析中首选的方法，但是它也有一些短板，比如在数据集中有脏数据时，由于其对每一个类的准则函数为平方误差，当样本数据中出现了不合理的极端值，会导致最终聚类结果产生一定的误差，而本篇将要介绍的K-medoids（中心点）聚类法在削弱异常值的影响上就有着其过人之处。

与K-means算法类似，区别在于中心点的选取，K-means中选取的中心点为当前类中所有点的重心，而K-medoids法选取的中心点为当前cluster中存在的一点，准则函数是当前cluster中所有其他点到该中心点的距离之和最小，这就在一定程度上削弱了异常值的影响，但缺点是计算较为复杂，耗费的计算机时间比K-means多。

具体的算法流程如下：

　　1.在总体n个样本点中任意选取k个点作为medoids

　　2.按照与medoids最近的原则，将剩余的n-k个点分配到当前最佳的medoids代表的类中

　　3.对于第i个类中除对应medoids点外的所有其他点，按顺序计算当其为新的medoids时，准则函数的值，遍历所有可能，选取准则函数最小时对应的点作为新的medoids

　　4.重复2-3的过程，直到所有的medoids点不再发生变化或已达到设定的最大迭代次数

　　5.产出最终确定的k个类

而在R中有内置的pam()函数来进行K-medoids聚类，下面我们对人为添加脏数据的样本数据集分别利用K-medoids和K-means进行聚类，以各自的代价函数变化情况作为评判结果质量的标准：

rm(list=ls())
library(Rtsne)
library(cluster)
library(RColorBrewer)
data1 <- matrix(rnorm(10000,mean=0,sd=0.7),ncol=10,nrow=1000)
data2 <- matrix(rnorm(10000,mean=8,sd=0.7),ncol=10,nrow=1000)
data3 <- matrix(rnorm(10000,mean=16,sd=0.7),ncol=10,nrow=1000)
data4 <- matrix(rnorm(200,mean=100,sd=0.5),ncol=10,nrow=20)
data <- rbind(data1,data2,data3,data4)

#数据降维
tsne <- Rtsne(data,check_duplicates = FALSE)
cols <- sample(brewer.pal(n=7,name='Set1'),7)

#自定义代价函数计算函数
Mycost <- function(data,medoids){
  l <- length(data[,1])
  d <- matrix(0,nrow=l,ncol=length(medoids[,1]))
  for(i in 1:l){
    for(j in 1:length(medoids[,1])){
      dist <- 0
      for(k in 1:length(medoids[1,])){
        dist <- dist + (data[i,k]-medoids[j,k])^2
      }
      d[i,j] <- dist
    }
  }
  return(sum(apply(d,1,min)))
}

par(mfrow=c(2,3))
#进行K-medoids聚类
cost <- c()
for(i in 2:7){
  cl <- pam(data,k=i)
  plot(tsne$Y,col=cols[cl$clustering])
  title(paste(paste('K-medoids Cluster of',as.character(i)),'Clusters'))
  cost[i-1] <- Mycost(data,cl$medoids)
}

par(mfrow=c(1,1))
plot(2:7,cost,type='o',xlab='k',ylab='Cost')
title('Cost Change of K-medoids')

#进行K-means聚类
cost <- c()
par(mfrow=c(2,3))
for(i in 2:7){
  cl <- kmeans(data,centers=i)
  plot(tsne$Y,col=cols[cl$cluster])
  title(paste(paste('K-means Cluster of',as.character(i)),'Clusters'))
  cost[i-1] <- Mycost(data,cl$centers)
}
par(mfrow=c(1,1))
plot(2:7,cost,type='o',xlab='k',ylab='Cost')
title('Cost Change of K-means')

K-medoids的聚类结果（基于不同的k值）：

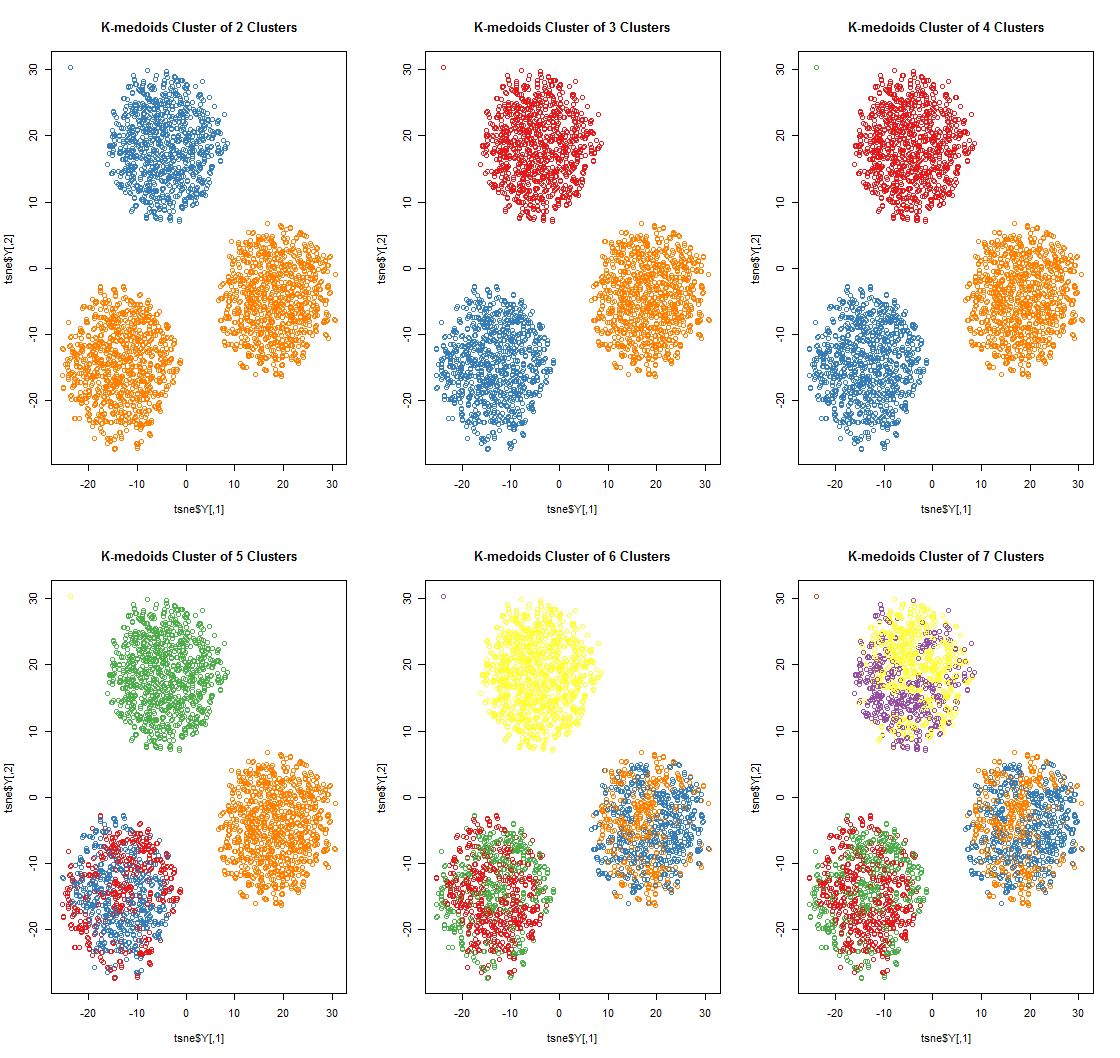
K-medoids过程的代价函数变化情况：

K-means的聚类结果（基于不同的k值）：

K-means的代价函数变化情况：

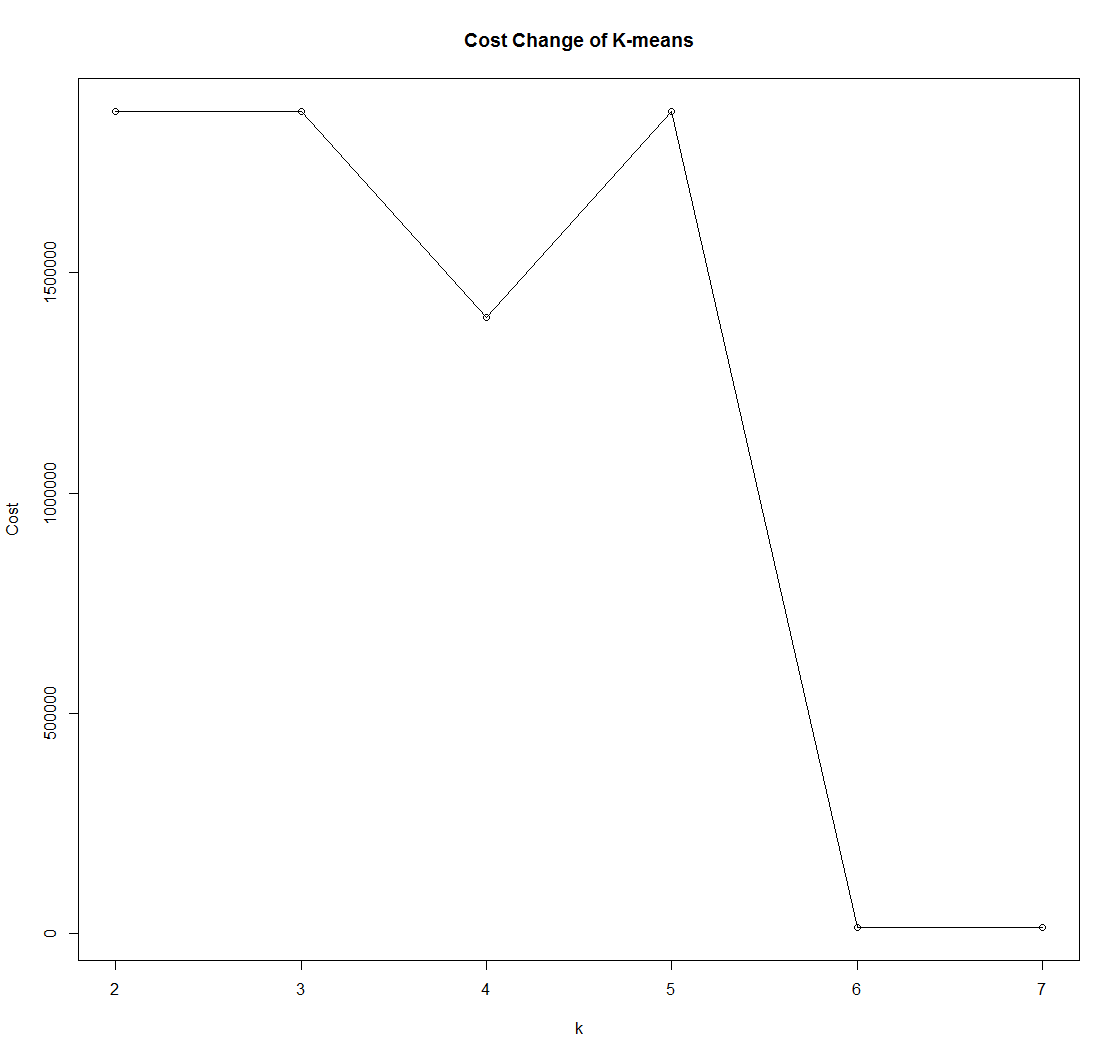
可以看出，K-medoids在应付含有脏数据的数据集时有着更为稳定的性能表现。

Python

在Python中关于K-medoids的第三方算法实在是够冷门，经过笔者一番查找，终于在一个久无人维护的第三方模块pyclust中找到了对应的方法KMedoids()，若要对制定的数据进行聚类，使用格式如下：
KMedoids(n_clusters=n).fit_predict(data),其中data即为将要预测的样本集，下面以具体示例进行展示：

from pyclust import KMedoids
import numpy as np
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt

'''构造示例数据集（加入少量脏数据）'''
data1 = np.random.normal(0,0.9,(1000,10))
data2 = np.random.normal(1,0.9,(1000,10))
data3 = np.random.normal(2,0.9,(1000,10))
data4 = np.random.normal(3,0.9,(1000,10))
data5 = np.random.normal(50,0.9,(50,10))

data = np.concatenate((data1,data2,data3,data4,data5))

'''准备可视化需要的降维数据'''
data_TSNE = TSNE(learning_rate=100).fit_transform(data)

'''对不同的k进行试探性K-medoids聚类并可视化'''
plt.figure(figsize=(12,8))
for i in range(2,6):
    k = KMedoids(n_clusters=i,distance='euclidean',max_iter=1000).fit_predict(data)
    colors = ([['red','blue','black','yellow','green'][i] for i in k])
    plt.subplot(219+i)
    plt.scatter(data_TSNE[:,0],data_TSNE[:,1],c=colors,s=10)
    plt.title('K-medoids Resul of '.format(str(i)))

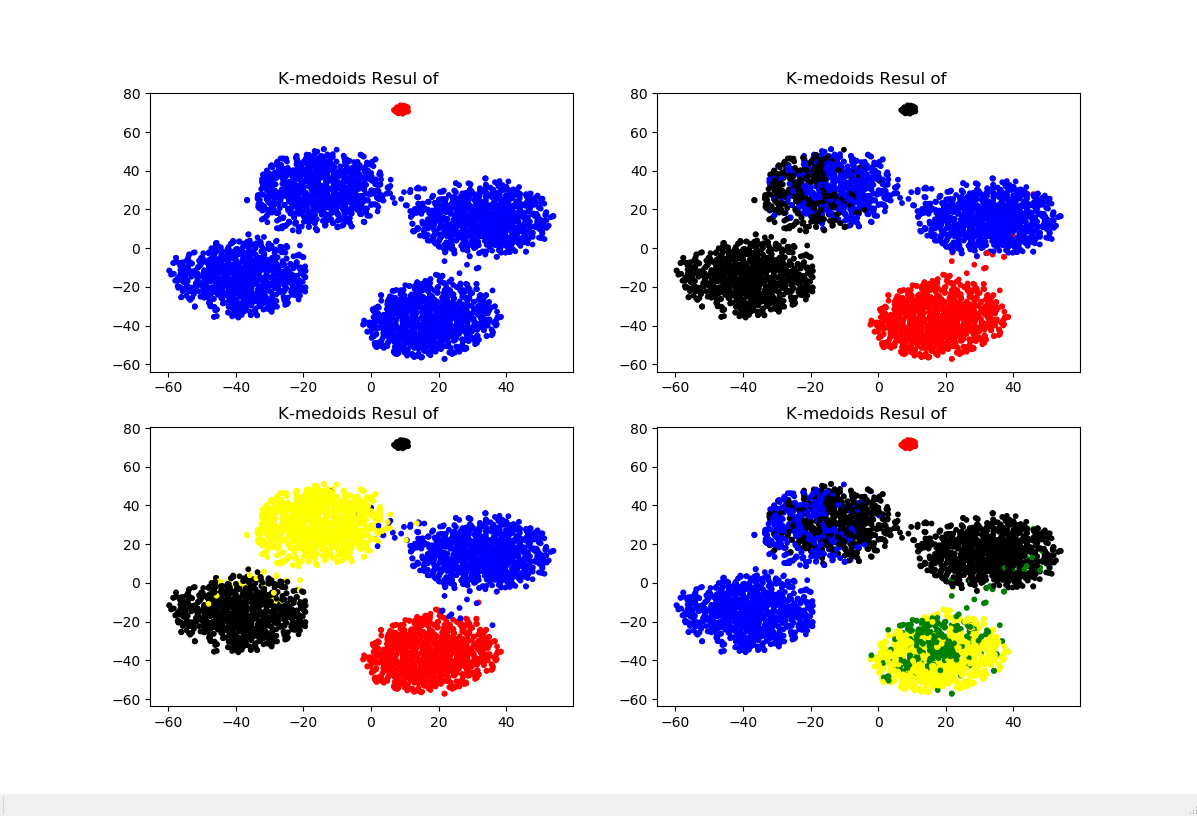
以上就是关于K-medoids算法的基本知识，如有错误之处望指出。