Machine Learning - week 2 - Multivariate Linear Regression
Multiple Features
上一章中,hθ(x) = θ0 + θ1x,表示只有一个 feature。现在,有多个 features,所以 hθ(x) = θ0 + θ1x1 + θ2x2 + ... + θjxj。
为了标记的方便,增加 x0 = 1
用向量表示
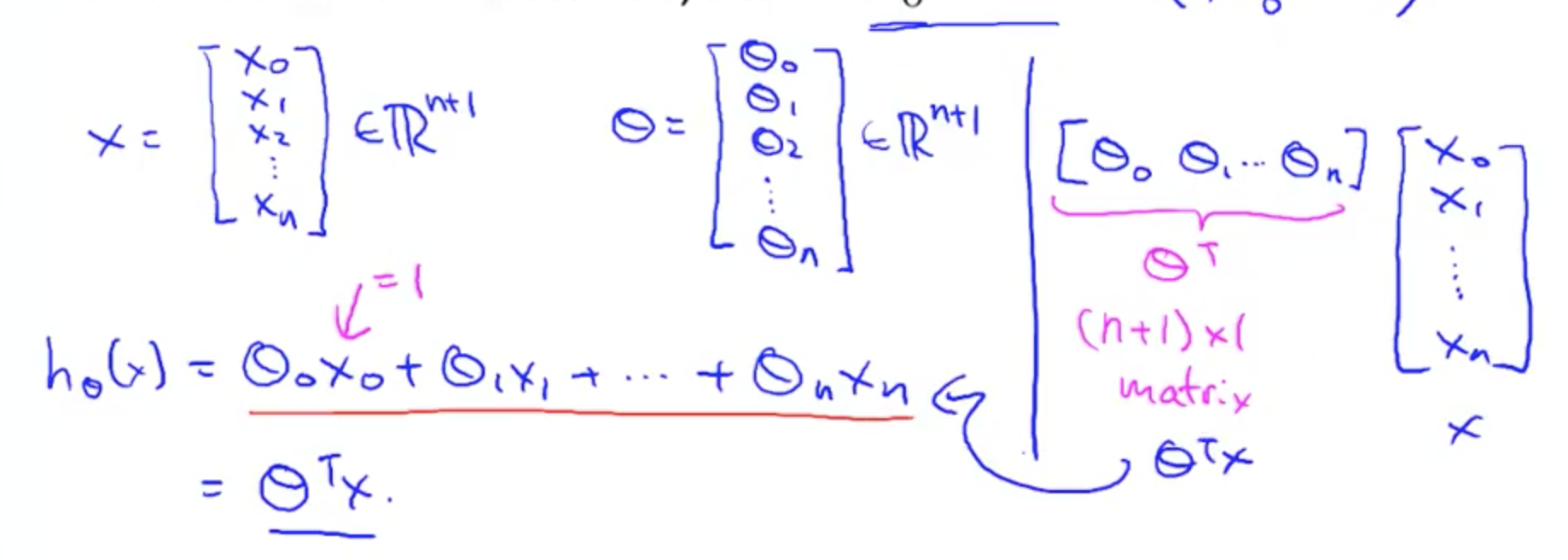
这里的 X 表示单行 Xi。如果是表示所有的 hθ(x),就会 X * θ(X 表示所有 x 的值)
Gradient Descent For Multiple Features 也是同理,扩展到 j 个,就不再赘述。
Gradient Descent in Practice - Feature Scaling
逻辑是:确保所有的 features 在同一尺度。尺度理解为相差不超过 10 倍或者百倍。
Features 的范围越小,总的可能性就越小,计算速度就能加快。
Dividing by the range
通过 feature/range 使每个 feature 大概在 [-1, 1] 的范围内
下题是一个例子:

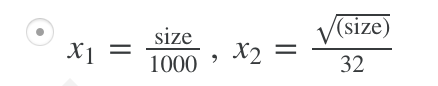
Mean normalization
将值变为接近 0。除了 x0,因为 x0 的值为 1。
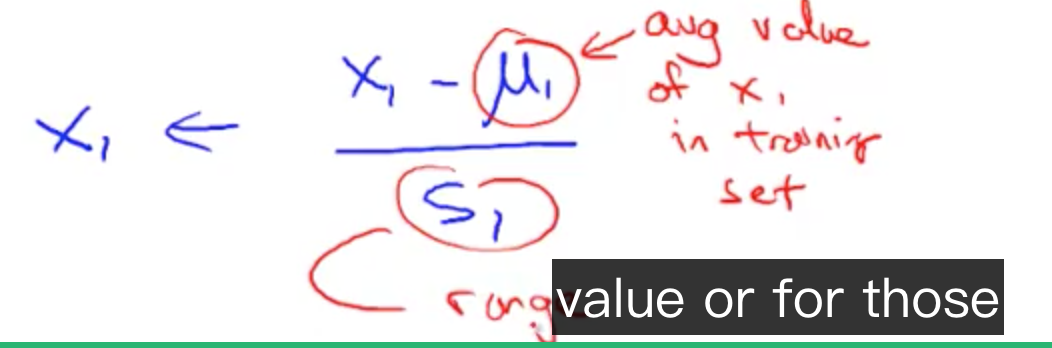
mu1 是 average value of x1 in trainning sets;
S1 是 x1 的范围大小,比如卧室是 [0, 5],那么范围为 5 - 0 = 5。也可以设置成标准差(在练习中就是这个)
需要将 x0 排除。
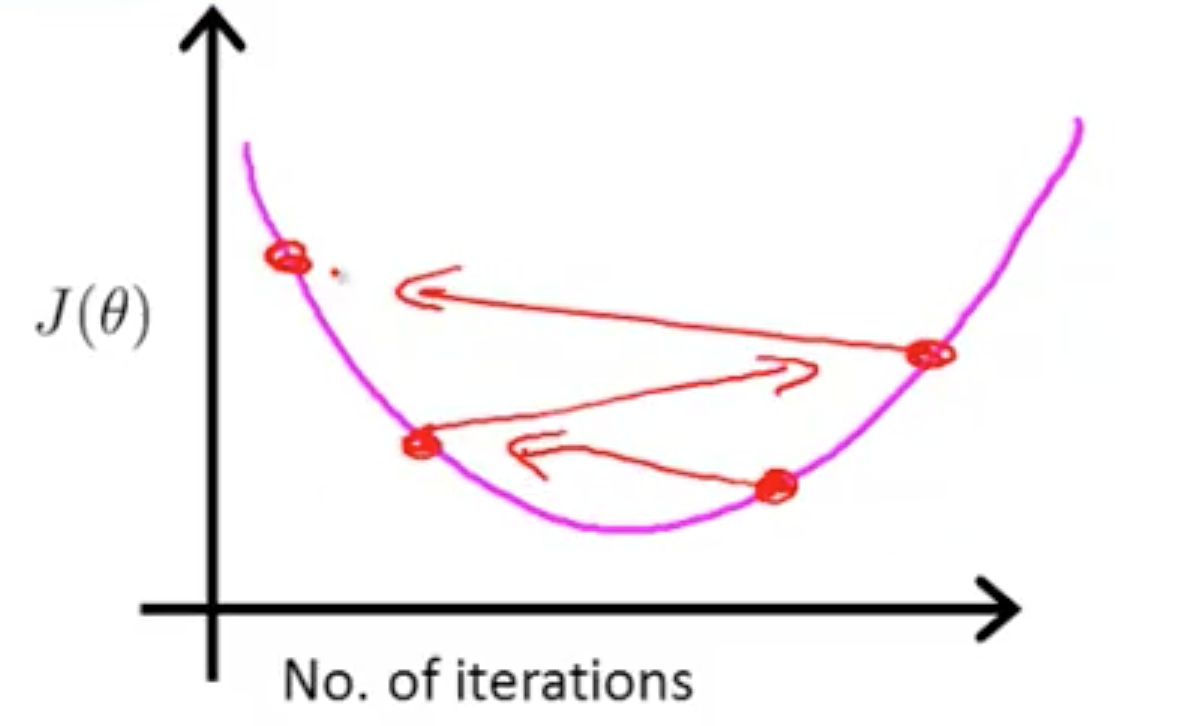
确保 gradient descent 工作正确

如上图,这个图像是正确的,随着循环次数的增加,J(θ) 主键减小。超过一定循环次数之后,J(θ) 曲线趋于平缓。可以根据图像得出什么时候停止,或者当每次循环,J(θ) 的变化小于 ε 时停止。
图像上升

说明 α 取值大了,应该减小。上图的图像另一种观看方式:
如果 α 足够小,那么能缓慢但完全覆盖。
如果 α 太大:在每次循环时,可能不会减少从而不能完全覆盖。
可以由程序来自动选择,后面会提到。
Features and polynomial regression
可以使用自定义的 features 而不是完全照搬已存在的 features。比如房子有长宽两个属性,我们可以创建一个新属性--面积。然后,表达式变成
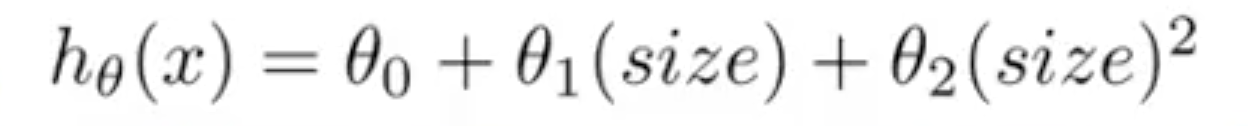 ,但是这个曲线是先减小后增大的,与实际数据不符(面积越大,总价越高)。所以调整为
,但是这个曲线是先减小后增大的,与实际数据不符(面积越大,总价越高)。所以调整为
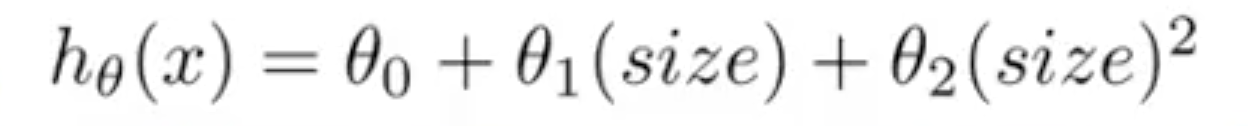 (可以调整表达式直到符合数据为止)。
(可以调整表达式直到符合数据为止)。
Normal equation
Gradient Descent 随着循环次数增加,逐步逼近最小值。如图:
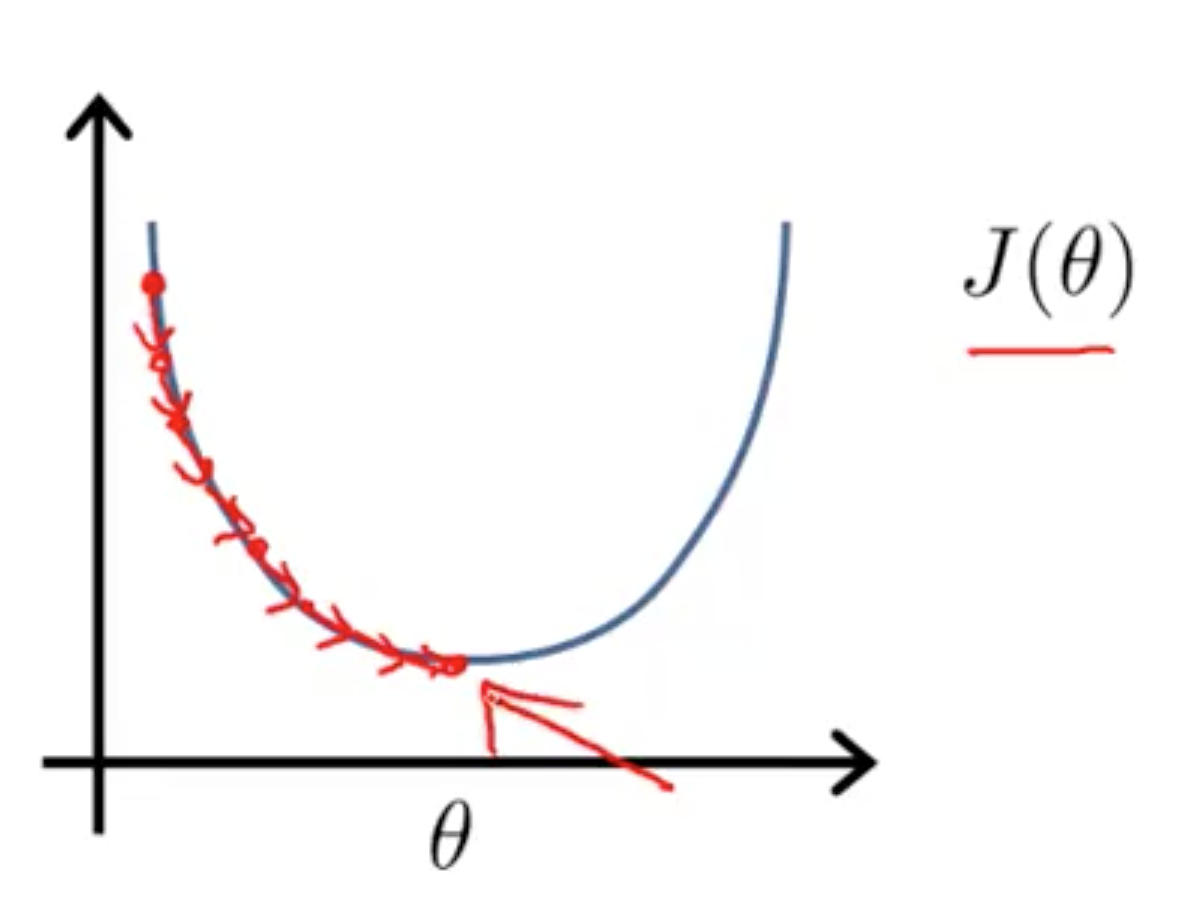
Normal equation 是通过方法直接计算出 θ。
导数为 0 时最小
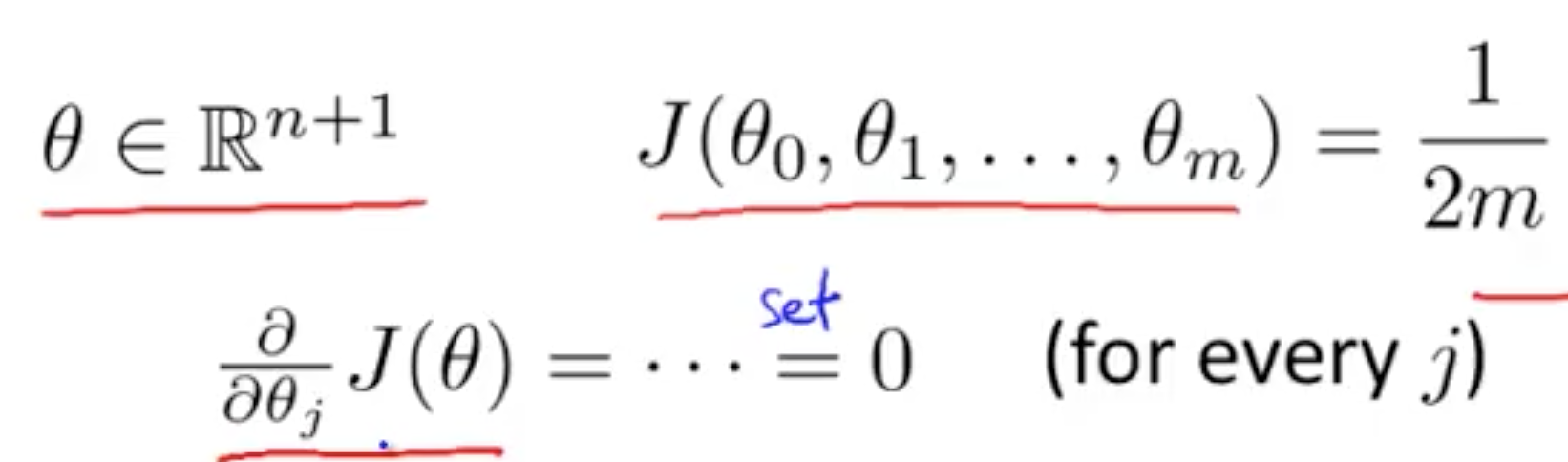
然后解出 θ0 到 θn
求解 θ 的方程
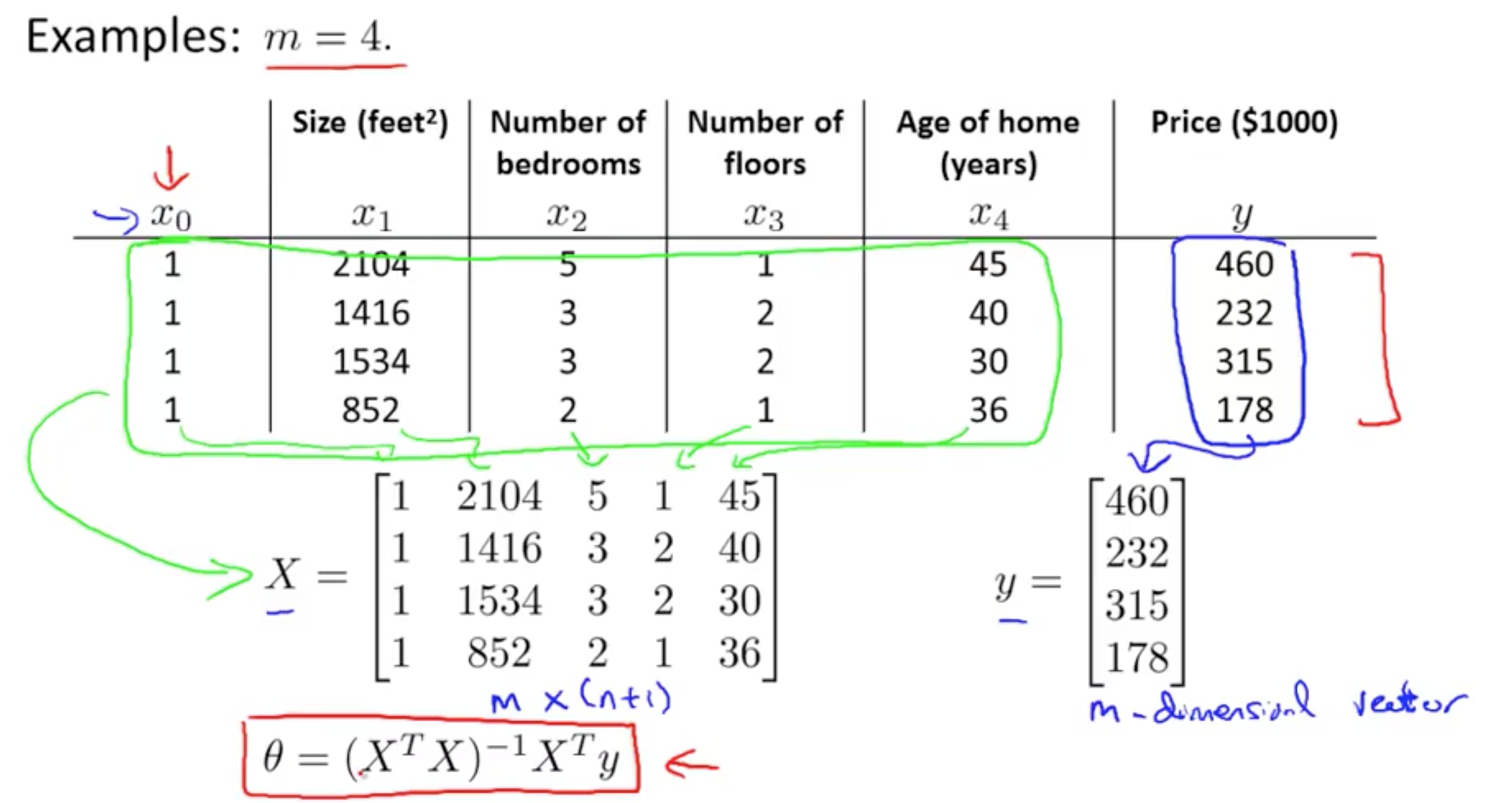
Matrix 概念见 Machine Learning - week 1
什么时候用 Gradient Descent 或者 Normal Equation

当 n 较大时,右边的会很慢,因为计算 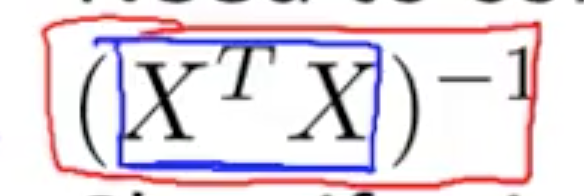 是 O(n3)
是 O(n3)
当 n 小的时候,右边会更快,因为它是直接得出结果,不需要 iterations 或者 feature scaling。
如果 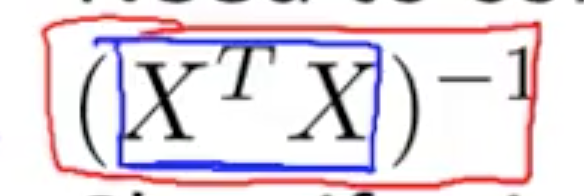 是 non-invertible?
是 non-invertible?
1. Redundant features (are not linearly independent).
E.g. x1 = size in feet2; x2 = size in m2
2. Too many features(e.g. m <= n)
比如 m = 10, n = 100,意思是你只有 10 个数据,但有 100 个 features,显然,数据不足以覆盖所有的 features。
可以删除一些 features(只保留与数据相关的 features)或者使用 regularization。
习题
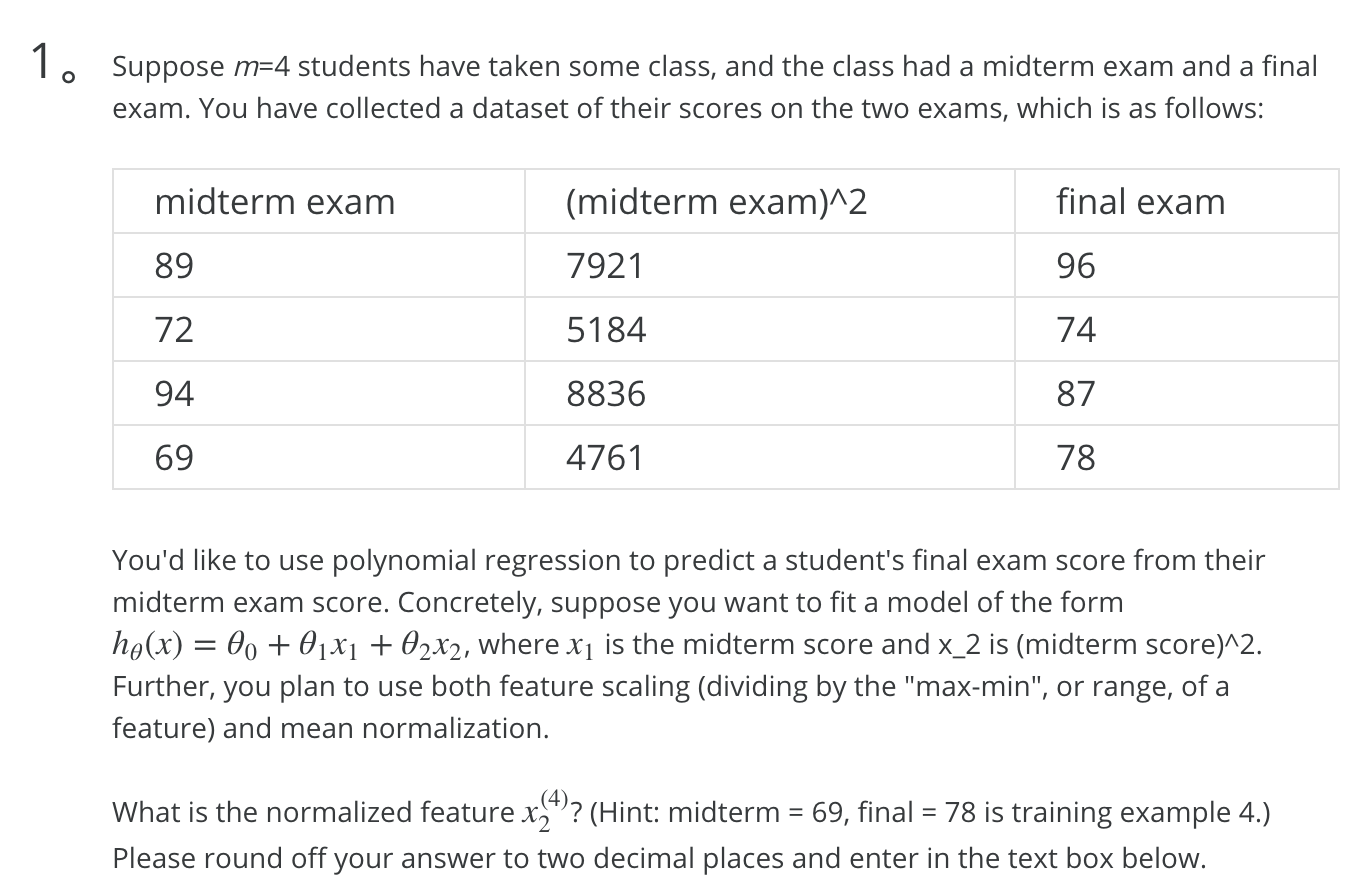
1. 
不知道如何同时使用两种方法,这两种方法是否是顺序相关的?
使用 Dividing by the range
range = max - min = 8836 - 4761 = 4075
vector / range 后变为
1.9438
1.2721
2.1683
1.1683
对上述使用 mean normalization
avg = 1.6382
range = 2.1683 - 1.1683 = 1
x2(4) = (1.1683 - 1.6382) / 1 = -0.46990 保留两位小数为 -0.47
5. 
上面提到了“Features 的范围越小,总的可能性就越小,计算速度就能加快。”(多选题也可以单选)
Octave Tutorial
介绍了 Octave 的常用语法。
Vectorization
使用 vectorization 会比 for loop 更加高效。
例子

更复杂的例子
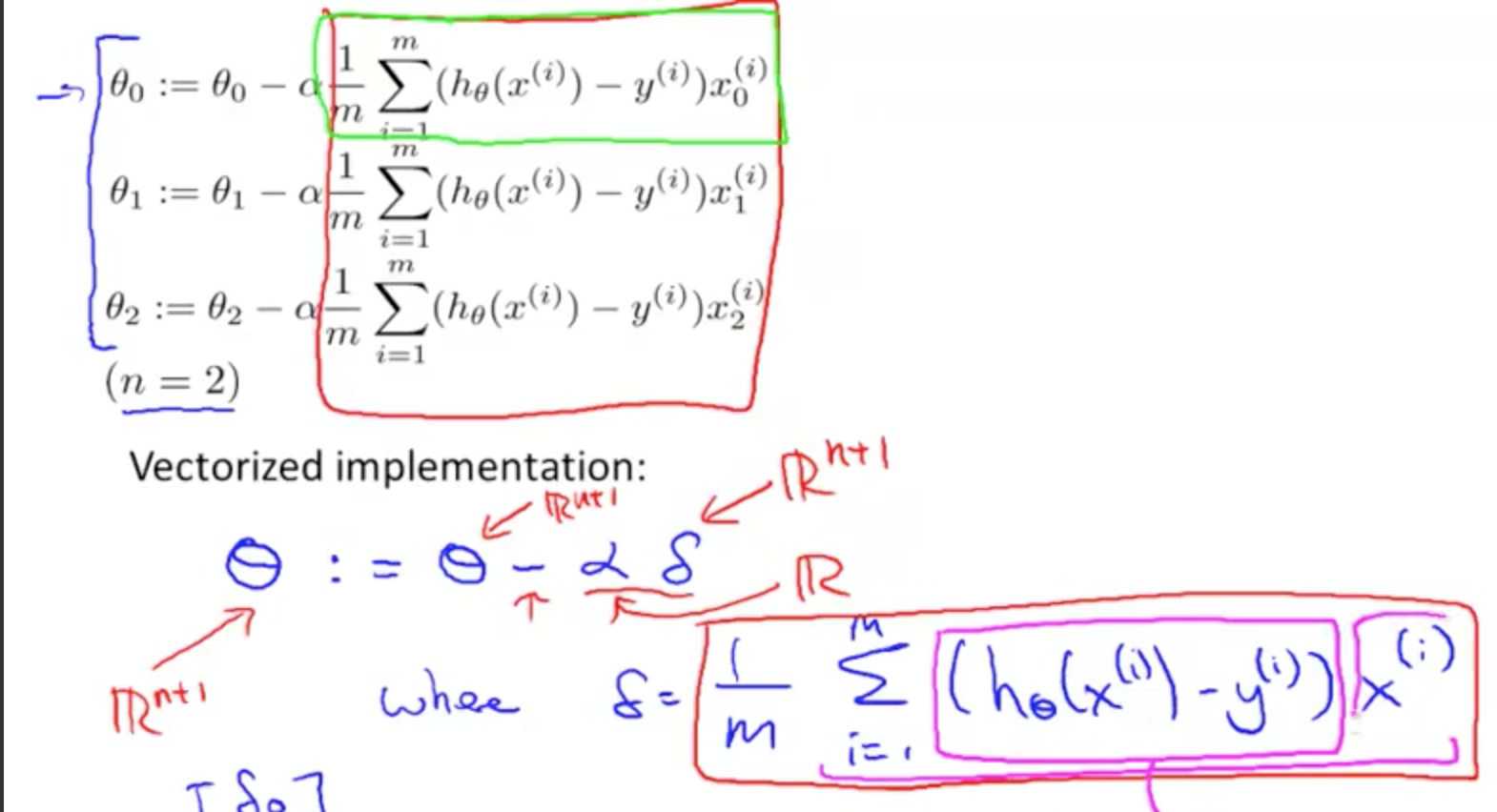
怎样把 delta vectorized 还没有理解。整体思想了解了。
Octave arithmetic operators 有一些不符合你的直觉。
比如 ^ 与 .^
X =
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
octave:80> X .^ 2
ans =
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
octave:81> X ^ 2
ans =
7 7 7 7 7 7 7
7 7 7 7 7 7 7
7 7 7 7 7 7 7
7 7 7 7 7 7 7
7 7 7 7 7 7 7
7 7 7 7 7 7 7
7 7 7 7 7 7 7
Machine Learning - week 2 - Multivariate Linear Regression的更多相关文章
- machine learning(14) --Regularization:Regularized linear regression
machine learning(13) --Regularization:Regularized linear regression Gradient descent without regular ...
- Andrew Ng 的 Machine Learning 课程学习 (week2) Linear Regression
这学期一直在跟进 Coursera上的 Machina Learning 公开课, 老师Andrew Ng是coursera的创始人之一,Machine Learning方面的大牛.这门课程对想要了解 ...
- Machine Learning 学习笔记2 - linear regression with one variable(单变量线性回归)
一.Model representation(模型表示) 1.1 训练集 由训练样例(training example)组成的集合就是训练集(training set), 如下图所示, 其中(x,y) ...
- [Machine Learning] 单变量线性回归(Linear Regression with One Variable) - 线性回归-代价函数-梯度下降法-学习率
单变量线性回归(Linear Regression with One Variable) 什么是线性回归?线性回归是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方 ...
- Multivariate Linear Regression
Multiple Features Linear regression with multiple variables is also known as "multivariate line ...
- Note for video Machine Learning and Data Mining——Linear Model
Here is the note for lecture three. the linear model Linear model is a basic and important model in ...
- 转载 Deep learning:三(Multivariance Linear Regression练习)
前言: 本文主要是来练习多变量线性回归问题(其实本文也就3个变量),参考资料见网页:http://openclassroom.stanford.edu/MainFolder/DocumentPage. ...
- Andrew Ng 的 Machine Learning 课程学习 (week3) Logistic Regression
这学期一直在跟进 Coursera上的 Machina Learning 公开课, 老师Andrew Ng是coursera的创始人之一,Machine Learning方面的大牛.这门课程对想要了解 ...
- Machine Learning in Action(4) Logistic Regression
从这节算是开始进入“正规”的机器学习了吧,之所以“正规”因为它开始要建立价值函数(cost function),接着优化价值函数求出权重,然后测试验证.这整套的流程是机器学习必经环节.今天要学习的话题 ...
随机推荐
- zoj 2744 - Palindromes
题目:统计一个串中的回文子串的个数(注意是子串,要连续). 分析:dp.暴力.直接用dp,二维数组内存不够用,并且dp木有暴力快( ⊙ o ⊙ )啊! 说明:(2011-09-24 03:22). # ...
- 一个下载git库代码的脚本
由于每日构建需求, 须要用脚本下载代码, 实现自己主动化编译, 这个脚本是整个系统的一小块功能 #!/bin/bash #@author Liuyang #@date 2015-06-23 funct ...
- 解析 PHP 中 session 的实现原理以及大网站应用应该注意的问题
一 PHP SESSION原理 session 是在服务器端保持用户会话数据的一种方法,而 cookie 是在客户端保持用户数据.HTTP 协议是一种无状态协议,服务器响应完之后就失去了与浏览器的联系 ...
- python 爬取王者荣耀高清壁纸
代码地址如下:http://www.demodashi.com/demo/13104.html 一.前言 打过王者的童鞋一般都会喜欢里边设计出来的英雄吧,特别想把王者荣耀的英雄的高清图片当成电脑桌面 ...
- prototype 用法
prototype使得js面向对象使用了prototype之后,使用它里面的属性或者函数 需要new出一个对象才可以使用.否则不使用prototype,直接向对象注入 function Person( ...
- Docker的Jenkins Pipeline工作流
原文地址:http://www.youruncloud.com/blog/127.html 分享主题 一个软件产品的开发周期中,尤其是敏捷开发,持续集成和持续部署是必不可少的环节,而随着产品的丰富,模 ...
- Python课程之字典
字典(dict) 一.定义:字典类型在其他语言中又称为map,是一种映射类型,并且{key:value}无序,其关键字必须为不可变类型(如:元组/字符串),在同一个字典中关键字必须互不相同(若出现相同 ...
- TCP/IP --概述
分层 网络协议通常分不同层次进行开发,每一层分别负责不同的通信功能.一个协议族,比如T C P / I P,是一组不同层次上的多个协议的组合.T C P / I P通常被认为是一个四层协议系统.,如图 ...
- vue 父组件如何调用子组件的函数Methods
答案就是使用ref即可. <countdown ref="countdown"></countdown> beforeDestroy () { // 切换页 ...
- Mysql又一次整理笔记--woods备忘
==============================SQL备忘 CRUD 查询 多表 事件等=============================== ------------------ ...
