【LuoguP1169 bzoj1057】[ZJOI2007]棋盘制作






















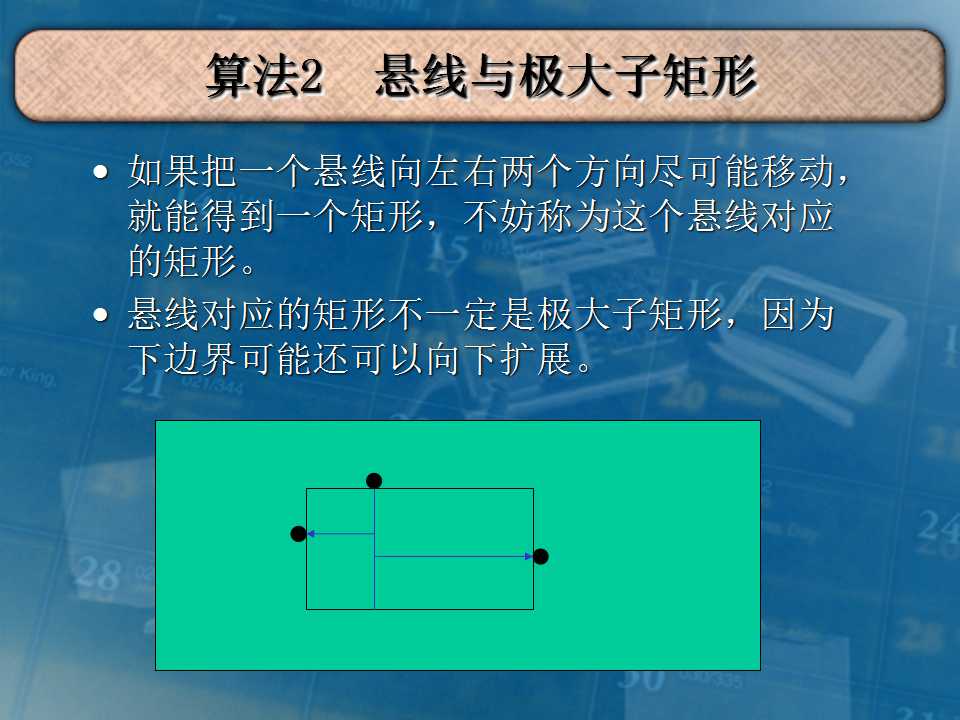



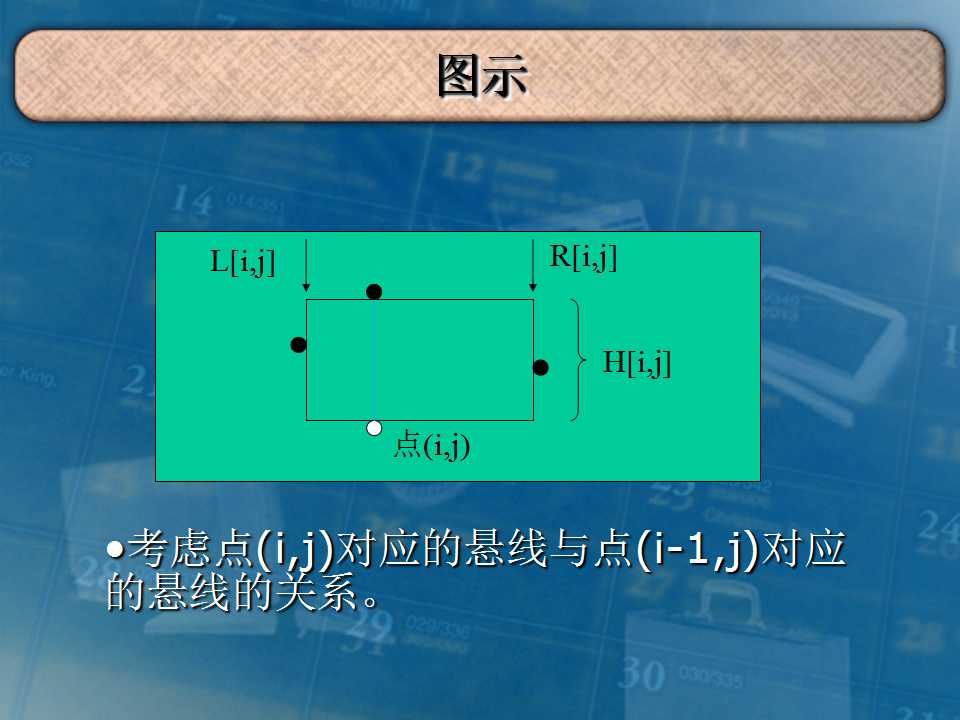


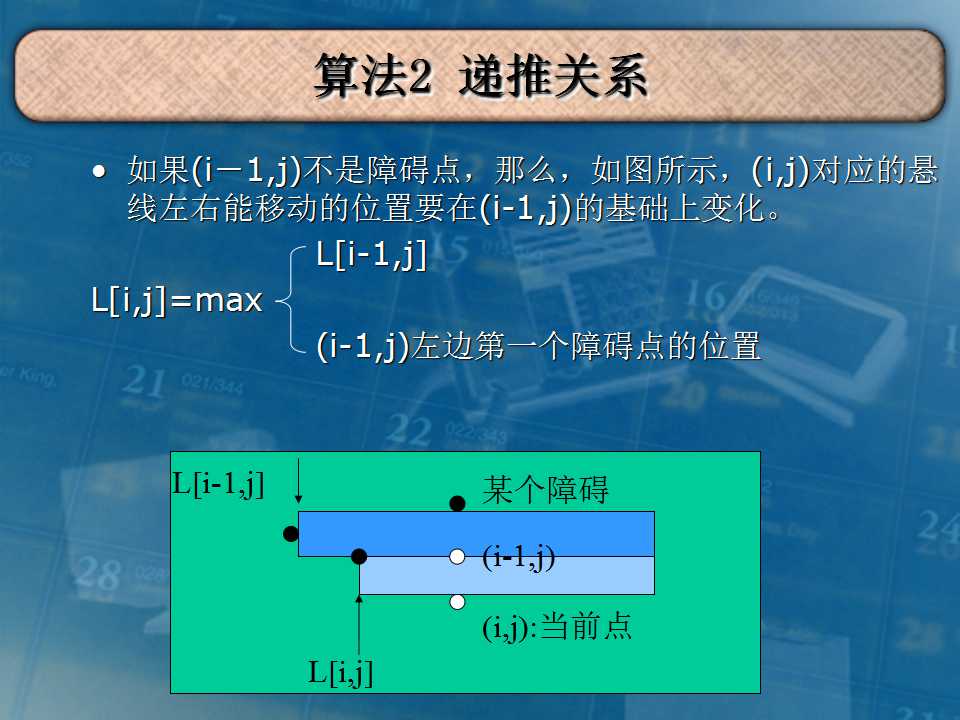
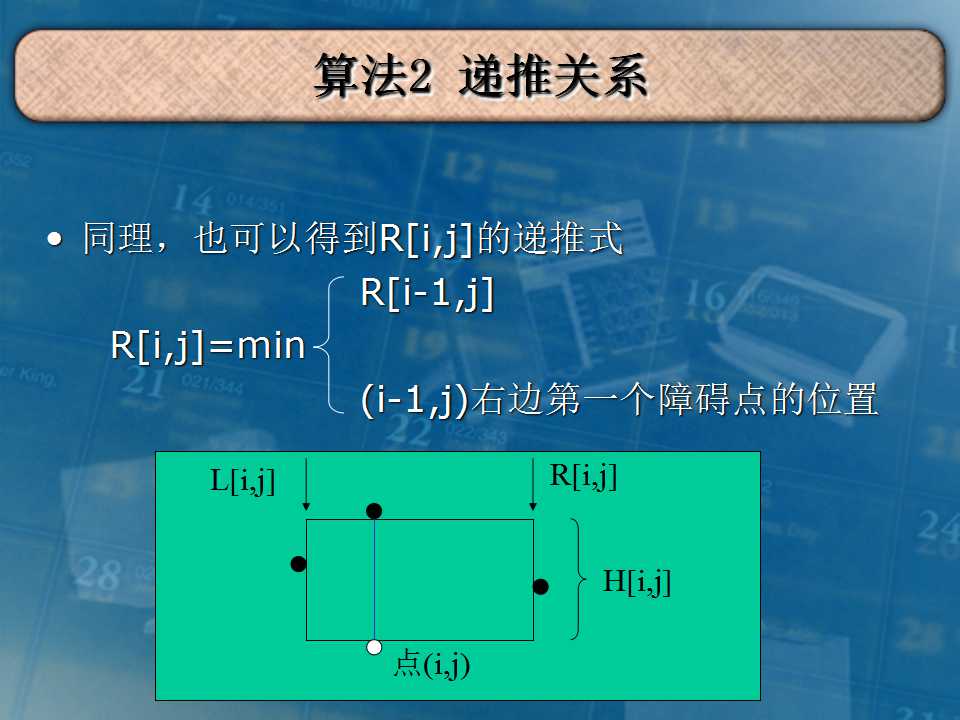








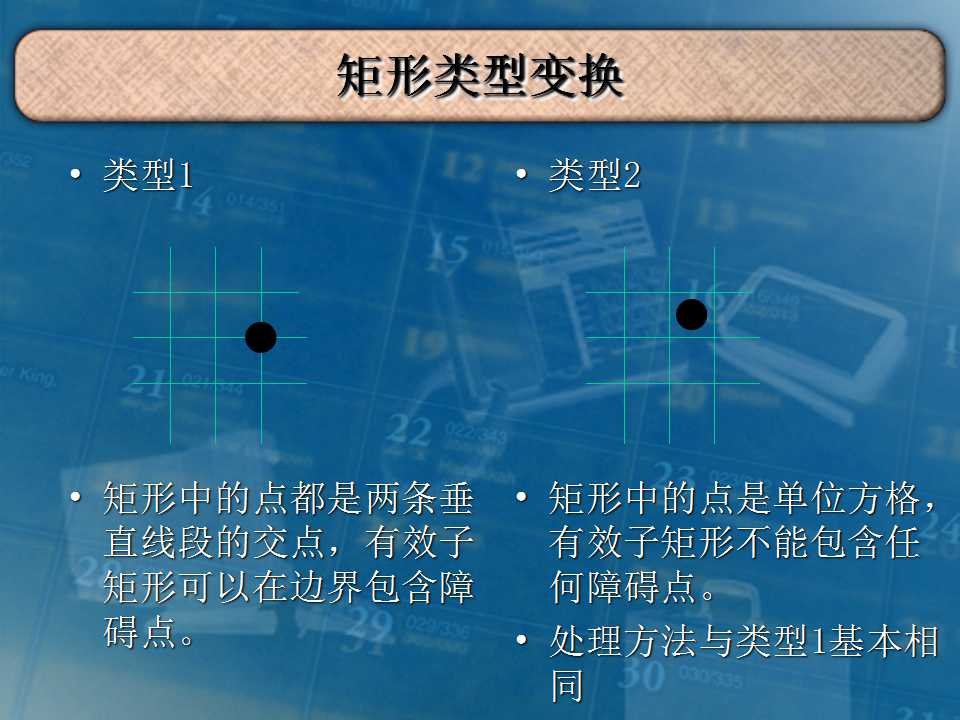
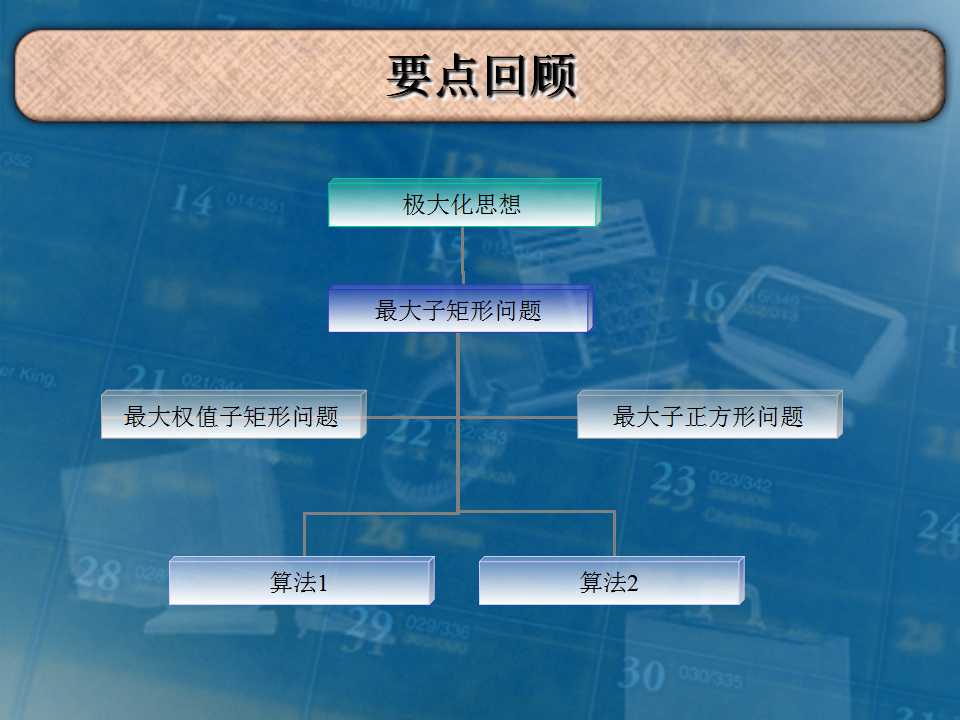
首先把矩阵转化一下,把横纵坐标和为偶数点的值取反,这样就转化成求最大的'0'或'1'矩阵。
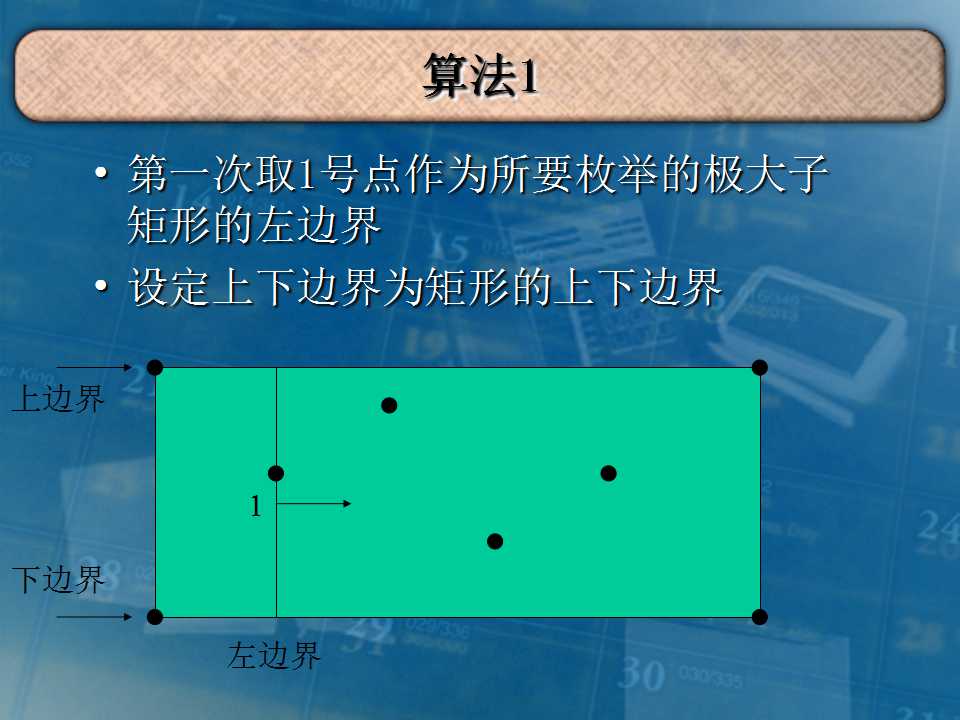
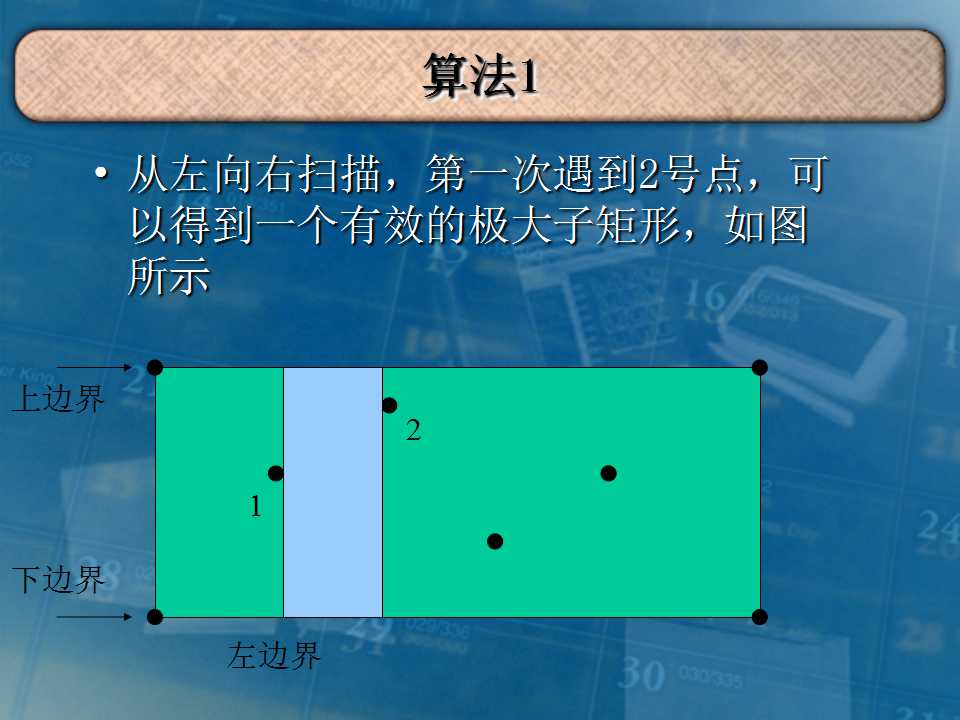
这道题每个数字是在格子内的,不能在边界包含障碍点。
求最大的0矩阵时,把1作为障碍点。求1同理。
然后求最接近的就可以用树状数组求解啦~
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std; const int N=,Inf=(int)1e9;
int n,m,a1,a2;
int a[N][N],l[N][N],r[N][N],last[N][N],cl[N][N],cr[N][N]; int minn(int x,int y){return x<y ? x:y;}
int maxx(int x,int y){return x>y ? x:y;} void add(int x,int y,int d)
{
for(int i=y;i<=m;i+=(i&(-i))) cl[x][i]=maxx(cl[x][i],d);
for(int i=y;i>=;i-=(i&(-i))) cr[x][i]=minn(cr[x][i],d);
} int get(int x,int y,int tmp)
{
if(tmp==)
{
int ans=;
for(int i=y-;i>=;i-=(i&(-i))) ans=maxx(ans,cl[x][i]);
if(ans==) return ;
else return ans+;
}
else
{
int ans=Inf;
for(int i=y+;i<=m;i+=(i&(-i))) ans=minn(ans,cr[x][i]);
if(ans>=Inf) return m;
else return ans-;
}
} void solve(int tmp)
{
memset(cl,,sizeof(cl));
memset(cr,,sizeof(cr));
for(int i=;i<=n;i++)
for(int j=;j<=m;j++)
{
if(a[i][j]==tmp) add(i,j,j);
}
memset(l[],,sizeof(l[]));
memset(r[],,sizeof(r[]));
for(int i=;i<=n;i++)
{
for(int j=;j<=m;j++)
{
if(a[i][j]==tmp) continue;
if(a[i-][j]==tmp)
{
l[i][j]=get(i,j,);//debug
r[i][j]=get(i,j,);//debug
last[i][j]=i-;
}
else
{
l[i][j]=maxx(l[i-][j],get(i,j,));
r[i][j]=minn(r[i-][j],get(i,j,));
last[i][j]=last[i-][j];
}
int xx=r[i][j]-l[i][j]+;
int yy=i-last[i][j];
a1=maxx(a1,minn(xx,yy)*minn(xx,yy));
a2=maxx(a2,xx*yy);
}
}
} int main()
{
freopen("a.in","r",stdin);
scanf("%d%d",&n,&m);
a1=;a2=;
for(int i=;i<=n;i++)
for(int j=;j<=m;j++)
{
scanf("%d",&a[i][j]);
if((i+j)%==) a[i][j]^=;
}
solve();
solve();
printf("%d\n%d\n",a1,a2);
return ;
}
【LuoguP1169 bzoj1057】[ZJOI2007]棋盘制作的更多相关文章
- BZOJ1057 [ZJOI2007]棋盘制作(极大化思想)
1057: [ZJOI2007]棋盘制作 Time Limit: 20 Sec Memory Limit: 162 MB Submit: 1848 Solved: 936 [Submit][Sta ...
- BZOJ1057 [ZJOI2007]棋盘制作 【最大同色矩形】
1057: [ZJOI2007]棋盘制作 Time Limit: 20 Sec Memory Limit: 162 MB Submit: 3248 Solved: 1636 [Submit][St ...
- BZOJ1057[ZJOI2007]棋盘制作 [单调栈]
题目描述 国际象棋是世界上最古老的博弈游戏之一,和中国的围棋.象棋以及日本的将棋同享盛名.据说国际象棋起源于易经的思想,棋盘是一个8*8大小的黑白相间的方阵,对应八八六十四卦,黑白对应阴阳. 而我们的 ...
- BZOJ1057 [ZJOI2007]棋盘制作
Description 国际象棋是世界上最古老的博弈游戏之一,和中国的围棋.象棋以及日本的将棋同享盛名.据说国际象棋起源 于易经的思想,棋盘是一个8*8大小的黑白相间的方阵,对应八八六十四卦,黑白对应 ...
- 洛谷 P1169||bzoj1057 [ZJOI2007]棋盘制作
洛谷P1169 bzoj1057 这个题目跟最大全0子矩阵是类似的.正方形的话,只要把任意极大子正方形(”极大“定义见后面的”论文“)当成把某个极大子矩形去掉一块变成正方形即可,容易解决. 解法1:看 ...
- 【单调栈 动态规划】bzoj1057: [ZJOI2007]棋盘制作
好像还有个名字叫做“极大化”? Description 国际象棋是世界上最古老的博弈游戏之一,和中国的围棋.象棋以及日本的将棋同享盛名.据说国际象棋起源 于易经的思想,棋盘是一个8*8大小的黑白相间的 ...
- bzoj1057: [ZJOI2007]棋盘制作 [dp][单调栈]
Description 国际象棋是世界上最古老的博弈游戏之一,和中国的围棋.象棋以及日本的将棋同享盛名.据说国际象棋起源 于易经的思想,棋盘是一个8*8大小的黑白相间的方阵,对应八八六十四卦,黑白对应 ...
- bzoj1057: [ZJOI2007]棋盘制作--最大子矩阵
既然要求最大01子矩阵,那么把应该为0的位置上的数取反,这样就变成求最大子矩阵 最大子矩阵可以用单调栈 #include<stdio.h> #include<string.h> ...
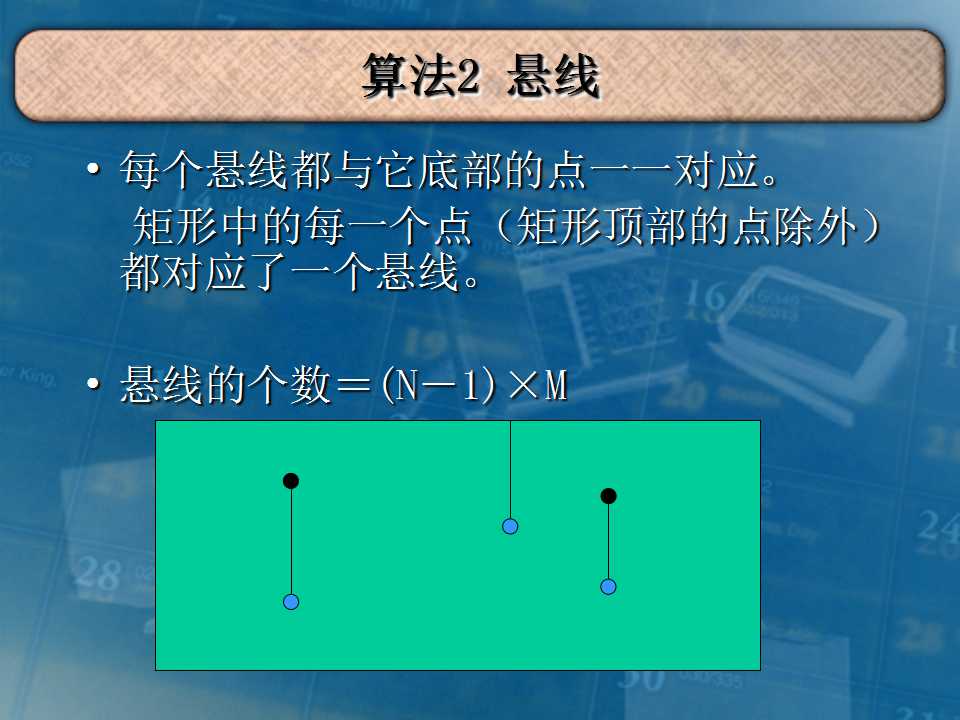
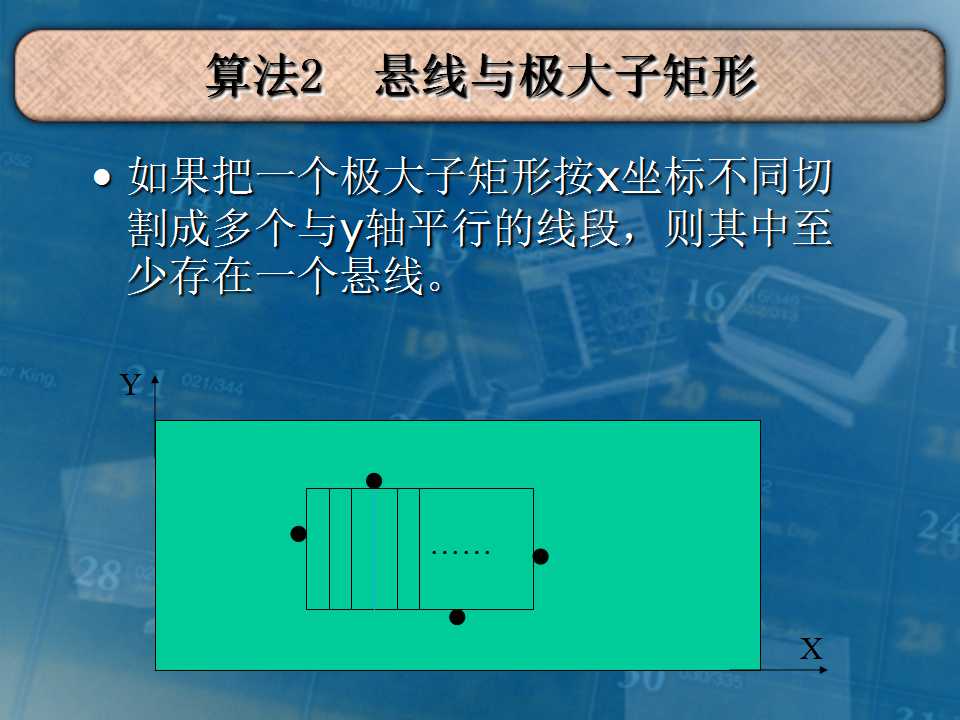
- 2018.10.19 bzoj1057: [ZJOI2007]棋盘制作(悬线法)
传送门 悬线法板题. 如果只求最大矩形面积那么跟玉蟾宫是一道题. 现在要求最大正方形面积. 所以每次更新最大矩形面积时用矩形宽的平方更新一下正方形答案就行了. 代码: #include<bits ...
- bzoj1057: [ZJOI2007]棋盘制作(悬线法)
题目要求纵横坐标和奇偶性不同的点取值不同,于是我们把纵横坐标和奇偶性为1的点和0的点分别取反,就变成经典的最大全1子矩阵问题了,用悬线法解决. #include<iostream> #in ...
随机推荐
- 让webapi支持CORS,可以跨域访问
1.在NuGet里搜索webapi找到下面的扩展,添加进项目里. 2.在Global.asax中添加一行代码 protected void Application_Start() { //添加CORS ...
- Fiddler安卓抓包详细教程
电脑端抓包一般图方便就用浏览器自带的,最近需要分析安卓一个APP的HTTP请求,尝试了wireshark(功能太强大了,然而我并不会用),tcpdump(用起来还是比较麻烦),网上搜了一下,还是使用F ...
- 从webview中加载assets中的html文件
private void readHtmlFormAssets(){ WebSettings webSettings = tipsWebView.getSettings(); webSettings. ...
- 剑指offer-用两个栈实现队列05
class Solution: def __init__(self): self.stackpush=[] self.stackpop=[] def push(self, node): # write ...
- Django,Celery, rabbitmq
学习Django 2 by Example书中的456页,运行 celery -A myshop worker -l info 报错.虽然特别指定了Celery的版本,也没用.之前使用的是标准安装:下 ...
- C++STL——set
一.相关定义 set 集合,有唯一性,即每一个元素只有一个: 是一个有序的容器,里面的元素都是排序好的: 支持插入,删除,查找等操作. 注意 set中的元素可以是任意类型的,但是由于需要排序,所以元素 ...
- php实现base64图片上传方式实例代码
<?php /** * base64图片上传 * @param $base64_img * @return array */ header("content-type:text/htm ...
- 如何在tracepoint上注册函数
register_trace_##name宏中 tracepoint_probe_register在这个函数中在同一个cp上可以挂多个处理函数, 查看函数:trace_block_rq_issue中定 ...
- click & copy
click & copy https://github.com/zenorocha/clipboard.js/issues/604 https://github.com/zenorocha/c ...
- 左右躲避障碍-神手ts版本
TypeScript-左右躲避障碍-神手 学习typescript,第一步应该是学习官方文档,理解最基础的语法.第二步开始用typescript实现一些js+css 或者canvas类型的游行.现在开 ...
