rm -f catalina.2018-10-22.*    与*号间无空格

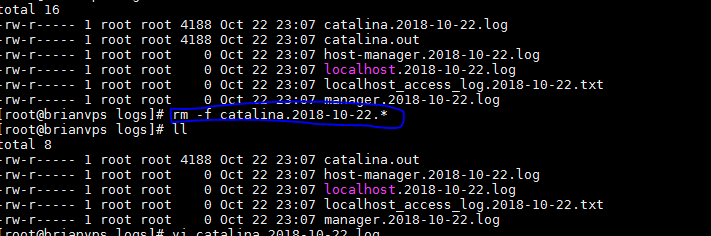
rm -f catalina.2018-10-22. *    :多了空格：

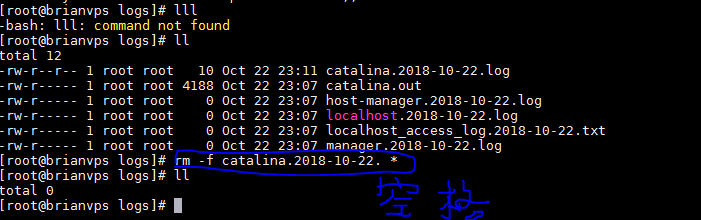
rm -f + 文件名+* 与 rm -f + 文件名* 的不同效果，大坑呀。的更多相关文章

  1. [RM HA3] Zookeeper在RM HA的应用

    [RM HA3] Zookeeper在RM HA的应用 RM HA(ResourceManager  HighAvailability)中使用Zookeeper的地方在ZKRMStateStore和Z ...

  2. Geometric regularity criterion for NSE: the cross product of velocity and vorticity 3: $u\times \f{\om}{|\om|}\cdot \f{\vLm^\be u}{|\vLm^\be u|}$

    在 [Chae, Dongho; Lee, Jihoon. On the geometric regularity conditions for the 3D Navier-Stokes equati ...

  3. HDU 1005 Number Sequence【斐波那契数列/循环节找规律/矩阵快速幂/求(A * f(n - 1) + B * f(n - 2)) mod 7】

    Number Sequence Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)T ...

  4. 函数$f(x+1)$和$f(x-1)$的奇偶性

    前言 廓清认知 1.函数\(y=f(x)\)的奇偶性 ①\(y=f(x)\)为奇函数,则满足\(f(-x)+f(x)=0\),即关于点\((0,0)\)对称: ②\(y=f(x)\)为偶函数,则满足\ ...

  5. xargs rm -rf 与 -exec rm

    # find ./ -exec rm {} \; # find ./ | xargs rm -rf 两者都可以把find命令查找到的结果删除,其区别简单的说是前者是把find发现的结果一次性传给exe ...

  6. 【.Net】C# 根据绝对路径获取 带后缀文件名、后缀名、文件名、不带文件名的文件路径

    1.c#根据绝对路径获取 带后缀文件名.后缀名.文件名.   1 string str =" F:\test\Default.aspx"; 2 string filename = ...

  7. F#之旅3 - F# PK C#:简单的求和

    原文链接:https://swlaschin.gitbooks.io/fsharpforfunandprofit/content/posts/fvsc-sum-of-squares.html Comp ...

  8. F#之旅1 - Why use F#?为什么要用F#？

    原文地址:http://fsharpforfunandprofit.com/why-use-fsharp/ Why use F#?Why you should consider using F# fo ...

  9. PHP多文件上传（二维数组$_FILES('文件域的名称')，move_uploaded_file（‘临时文件名’，‘新的文件名’））

    <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/ ...

随机推荐

  1. RequireJS 2.0 正式发布

    就在前天晚上RequireJS发布了一个大版本,直接从version1.0.8升级到了2.0.随后的几小时James Burke又迅速的将版本调整为2.0.1,当然其配套的打包压缩工具r.js也同时升 ...

  2. 安装 VS 2015 Update 2 + Windows SDK Tools 1.3.1 + Windows SDK 10586.212 后提示找不到 10586.0 SDK 问题的解决方法

    将 Visual Studio 2015 升级到 Update 2,并安装 Windows SDK Tools 1.3.1 和 Windows SDK 10586.212 后,有可能造成原本已安装的 ...

  3. python中的字符串 列表 字典

    字符串     一个有序的字符集合  不可变 1,可以使用for in语句进行迭代循环,返回元素    2,in类是于str.find()方法但是是返回布尔结果        str.find()返回 ...

  4. Java集合篇一：ArrayList

    package com.test.collection; /** * 自定义ArrayList容器 * * 1.实现原理:底层封装数组 * * 2.查询 * LinkList 相较 ArrayList ...

  5. Android 笔记之 R 文件

    Android笔记之R文件 h2{ color: #4abcde; } a{ color: blue; text-decoration: none; } a:hover{ color: red; te ...

  6. 禁止IOS双击上滑

    var agent = navigator.userAgent.toLowerCase(); var iLastTouch = null; if (agent.indexOf("iphone ...

  7. js 常用排序整理

    排序: 1. 内部排序: (1). 交换排序: 1). 冒泡排序 稳定 一次比较相邻两个元素的大小,顺序错误的,将其位置互换 (从高位到低位 或者 从低位到高位) 初始版: var array = [ ...

  8. matlab练习程序（单源最短路径Dijkstra）

    图的相关算法也算是自己的一个软肋了,当年没选修图论也是一大遗憾. 图像处理中,也有使用图论算法作为基础的相关算法,比如图割,这个算法就需要求最大流.最小割.所以熟悉一下图论算法对于图像处理还是很有帮助 ...

  9. mysql 省市数据

    CREATE TABLE `province` ( `id` ) DEFAULT NULL, `name` ) DEFAULT NULL ) ENGINE=INNODB DEFAULT CHARSET ...

  10. oracle 表 视图 存储过程 序列 job

    table 表 --delete table drop table Test1; -- Create table create table TEST1 (   ID     NUMBER,   T_N ...