咬文嚼图式的介绍二叉树、B树/B-树

前言

因为本人天资愚钝，所以总喜欢将抽象化的事务具象化表达。对于各类眼花缭乱的树，只需要认知到它们只是一种数据结构，类似数组，切片，列表，映射等这些耳熟能详的词汇。对于一个数据结构而言，无非就是增删改查而已，既然各类树也是数据结构，它们就不能逃离增删改查的桎梏。

那么，为什么我们需要树这种数据结构呢，直接用数组不行吗，用切片不行吗？当然可以，只不过现实世界是缤纷杂乱的，而又没有一种万能药式的数据结构以应对千变万化的业务需求。所以，才会有各类树，而且一些“高级”数据结构是基于树形数据结构的，例如映射。

二叉树

在中文语境中，节点结点傻傻分不清楚，故后文以 node 代表 "结点"，root node 代表根节点，child node 代表 “子节点”

二叉树是诸多树状结构的始祖，至于为什么不是三叉树，四叉树，或许是因为计算机只能数到二吧，哈哈，开个玩笑。二叉树很简单，每个 node 最多存在两个 child node，第一个节点称之为 root node。

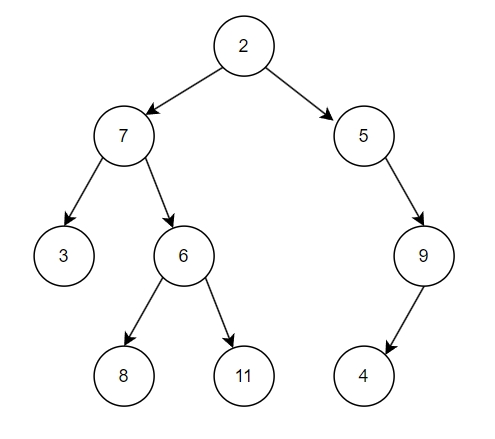
二叉树具备着一些基本的数学性质，不过很简单，定义从 i 从 0 开始：

第 i 层至多有 2ⁱ 个 node；
深度为 i 层二叉树至多有 2ⁱ⁺¹-1 个 node。

二叉树的特殊类型

这里有兴趣的可以了解一下，不影响后文的阅读。二叉树根据 child node 的不同，衍生出了几种特殊类型：在一颗二叉树中，如果每个 node 都有 0 或 2 个 child node，则二叉树是满二叉树；定义从 i 从 0 开始，一棵深度为 i，且仅有 2ⁱ⁺¹−1 个 node 的二叉树，称为完美二叉树；若除最后一层外的其余层都是满的，并且最后一层要么是满的，要么在右边缺少连续若干 node，则此二叉树为完全二叉树。

二叉搜索树

二叉搜索树（Binary Search Tree），也叫二叉查找树，有序二叉树，排序二叉树（名字还挺多）。它是一种常用且特殊的二叉树，它具备一个特有的性质，left node（左结点）始终小于 parent node (父结点)，right node 始终大于 parent node。

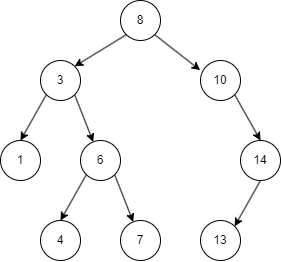
二叉搜索树的查找

二叉搜索树从 root node 开始，如果命中则返回；
否则，目标值比 node 小进入 left node；
比 node 大进入 right node；
如果左右都为空，则未命中。

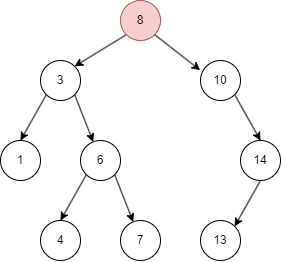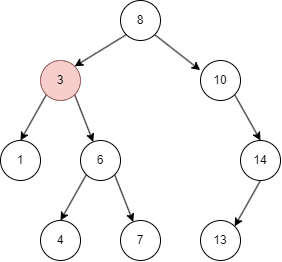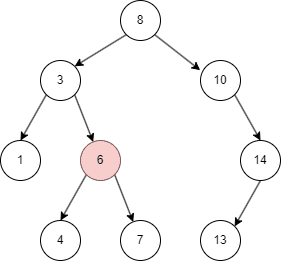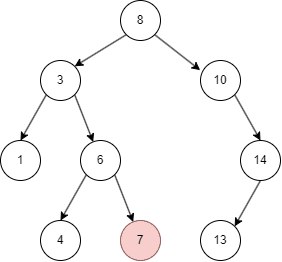
二叉搜索树的遍历

二叉搜索树有不同的遍历方式，这里介绍常用的中序遍历方式：

先遍历左子树；
然后查找当前左子树的 parent node；
遍历右子树。

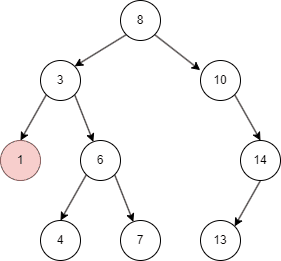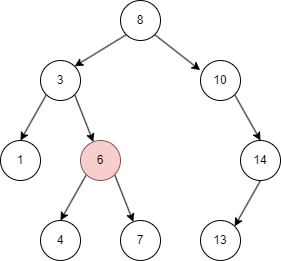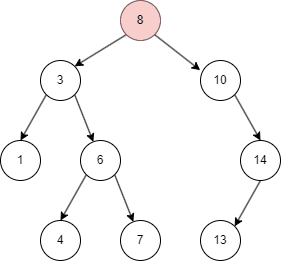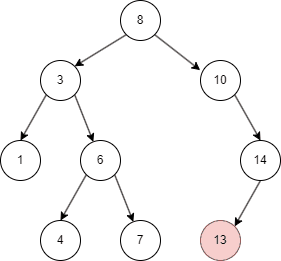
二叉搜索树的插入

二叉搜索树从 root node 开始，如果命中则不进行操作；
否则，目标值比 node 小进入 left node；
比 node 大进入 right node；
最终将值插入搜索停止的地方。

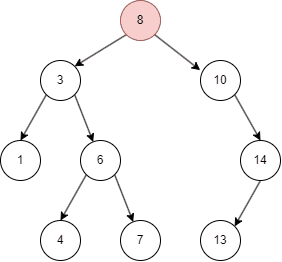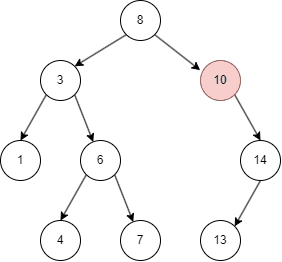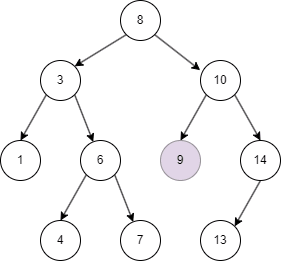
二叉搜索树的删除

二叉树的删除和查询基本一致，只要在命中时删除即可。

二叉搜索树从 root node 开始，如果命中则删除；
否则，目标值比 node 小进入 left node；
比 node 大进入 right node；
删除后使用该 node 左子树最大值或者右子树最小值替代该 node。

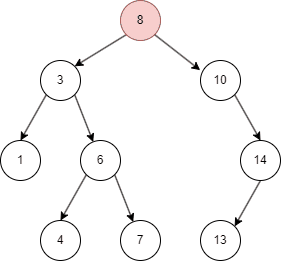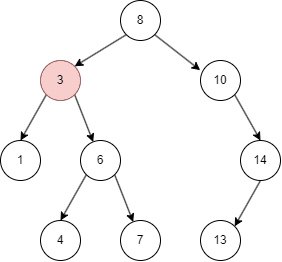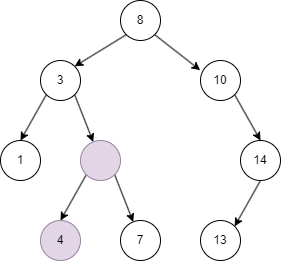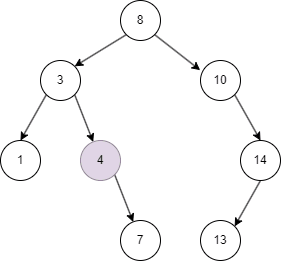
自平衡二叉树

从上面的几张动图中我们知晓，二叉搜索树不同于线性结构，它可以大大降低查找，插入的时间复杂度。但在特殊情况下，二叉搜索树可能退化为线性结构，假如我们依次插入1，2，3，4，5：

此时，二叉搜索树退化为线性结构，效率重新变回遍历。于是，便出现了自平衡二叉树，例如 AVL 树，红黑树，替罪羊树等。但它们并不是本文重点，下面我要介绍的是另外一种很常见的自平衡二叉树：B树。

B树

B树和B-树是同一个概念。B树相对于二叉树有两点最大的不同：

每个 node 可以有不止一个数值
每个 node 也可以有不止两个 child node

B树有两种类型 node：

internal node(内部结点)：不仅仅存储数据，也具备 child node；
leaf node(叶子结点)：仅存储数据，不具备 child node。

这两种 node 不同于前文所提的 root node 和 child node。root 和 child 是相对于阶层的概念，而 internal 和 leaf 是相对于性质的概念

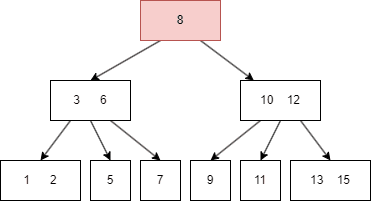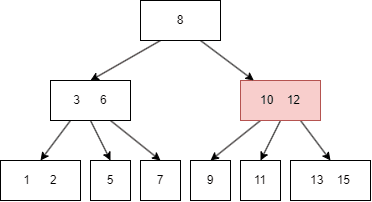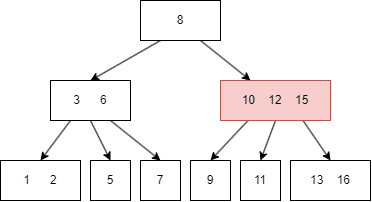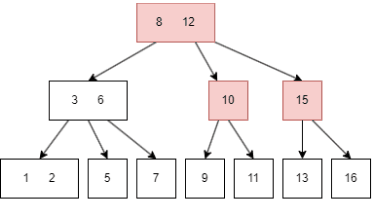
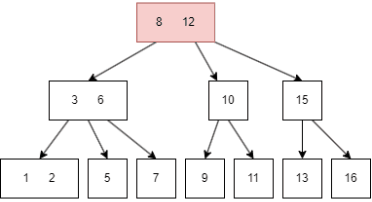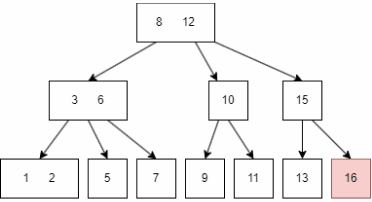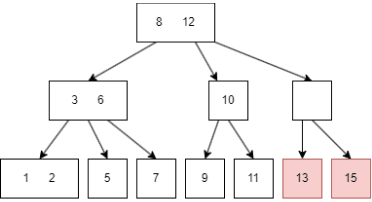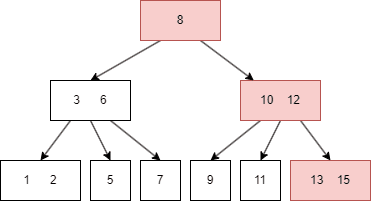
一个简单的图例如下：

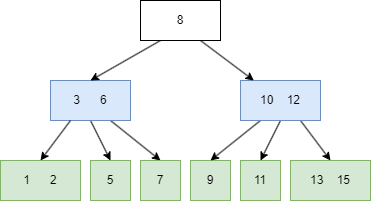
图中的蓝色方块是 internal node，绿色则是 leaf node。

B树有一些需要满足的性质，这里的抽象的逻辑有些烧脑，我会对照前面的图片来解释。设定一颗 m 阶的B树，m = 3：

设 internal node 的 child node 个数为 k：

如果 internal node 是 root node，那么 k = [2, m]，比如上图的 8 有两个 child node（3|6, 10/12）；
如果 internal node 不是 root node，那么 k = [m/2, m]，m/2 向上取整，比如上图的 3|6 有三个 child node；
如果 root node 的 k 为 0，那么 root node 是 leaf 类型的；
所有 leaf node 在同一层，上图最后一行的六个 node。

设任意 node 键值个数为 n：

对于 internal node， n = k-1，升序排序，满足 k[i] < k[i+1]，比如上图的三个 internal(8，3|6，10|12) 都满足此规律；
对于 leaf node，n = [0, m-1]，同样升序排序，比如上图最后一个的六个 leaf，其键值最多为两个。

上述的概念有些抽象，但是这是理解B树关键的地方所在，后面在B树的插入讲解，会有更多具象的动图来解释这些概念。

B树的查找

B树的查找类似于二叉树：

从 root node 开始，如果目标值小于 root node，进入左子树，否则进入右子树；
遍历 child node 的多个键值；
如果匹配到键值，则返回；
如果不匹配，则根据目标值的范围选择对应的子树；
重复步骤2、3、4，直到匹配成功返回或者未找到。

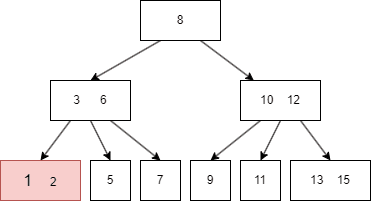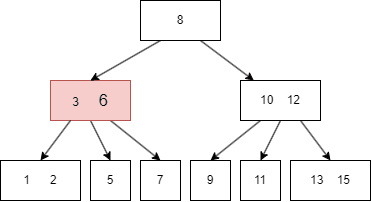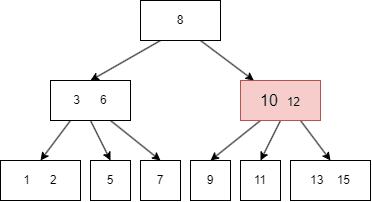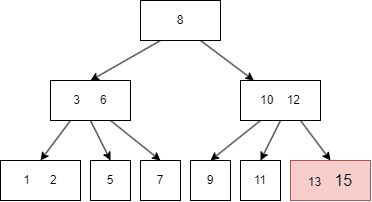
假如我们要查找 11：

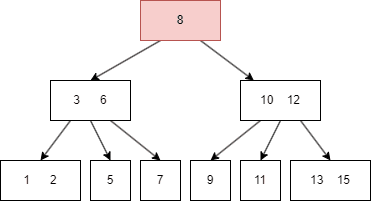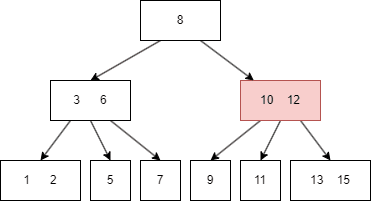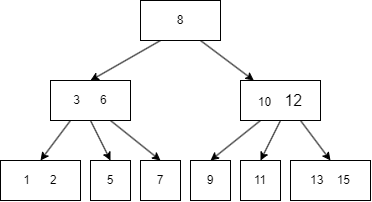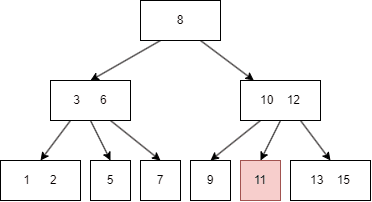
B树的遍历

B树的遍历方式类似二叉搜索树，不过因为B树一个 node 有多个键值和多个 child node，所以需要遍历每个左右子树和键值：

先遍历第一个左子树，也就是 parent node 第一个键值的左边；
然后查找当前 parent node 的第一个键值；
遍历第二个左子树，也就是 parent node 第二个键值的左边；
遍历完搜索的左子树，最后遍历当前 parent 的最右子树，即最后一个键值的右边。

B树的插入

插入前面的过程和查询一致，在插入后可能需要重整 node，以符合B树的性质，例如插入 16：

先查找到目标 node，也就是 13|15；
因为这是一颗 3 阶B树，所以 node 最多只能有两个键值，于是向上传递中间值 15；
parent node 最多也只能有两个键值，于是继续向上传递中间值 12；
此时 root node 是 8|12，需要有三个 child node，于是 10|15 需要拆分，再向下进一步调整，至此，插入 16 完成。

B树的删除

删除是插入的逆操作，但是往往比插入更复杂，因为删除后经常需要重整 node：

先查找到目标 node，也就是 16；
删除 16，此时 15 child node 剩下一个，不符合条件，递归向上调整，一直到根节点；
直到所有的条件都满足后，删除 16 完成。