HDU4686 Arc of Dream —— 矩阵快速幂

题目链接：https://vjudge.net/problem/HDU-4686

Arc of Dream

Time Limit: 2000/2000 MS (Java/Others)    Memory Limit: 65535/65535 K (Java/Others)
Total Submission(s): 5506    Accepted Submission(s): 1713

Problem Description

An Arc of Dream is a curve defined by following function:

where
a₀ = A0
a_i = a_i-1*AX+AY
b₀ = B0
b_i = b_i-1*BX+BY
What is the value of AoD(N) modulo 1,000,000,007?

 

Input

There are multiple test cases. Process to the End of File.
Each test case contains 7 nonnegative integers as follows:
N
A0 AX AY
B0 BX BY
N is no more than 10¹⁸, and all the other integers are no more than 2×10⁹.

 

Output

For each test case, output AoD(N) modulo 1,000,000,007.

 

Sample Input

1
1 2 3
4 5 6
2
1 2 3
4 5 6
3
1 2 3
4 5 6

 

Sample Output

4
134
1902

 

Author

Zejun Wu (watashi)

 

Source

2013 Multi-University Training Contest 9

题解：

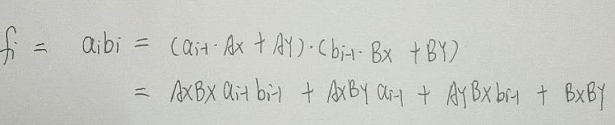
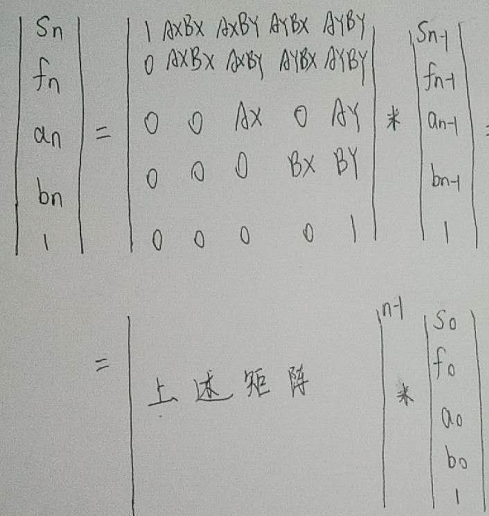
学习之处：

矩阵所要维护的，要么为变量，要么为常数1，而不是变量再乘上一个系数，或者是一个非1的常数。因为：假如变量需要乘上一个系数，那么可以在n*n矩阵中乘上。同样，如果变量需要加上一个常数，那么在对应1的位置，填上这个常数即可。

代码如下：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <cmath>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 using namespace std;
 typedef long long LL;
 const int INF = 2e9;
 const LL LNF = 9e18;
 const int MOD = 1e9+;
 const int MAXN = 1e6+;

 const int Size = ;
 struct MA
 {
     LL mat[Size][Size];
     void init()
     {
         for(int i = ; i<Size; i++)
         for(int j = ; j<Size; j++)
             mat[i][j] = (i==j);
     }
 };

 MA mul(MA x, MA y)
 {
     MA ret;
     memset(ret.mat, , sizeof(ret.mat));
     for(int i = ; i<Size; i++)
     for(int j = ; j<Size; j++)
     for(int k = ; k<Size; k++)
         ret.mat[i][j] += 1LL*x.mat[i][k]*y.mat[k][j]%MOD, ret.mat[i][j] %= MOD;
     return ret;
 }

 MA qpow(MA x, LL y)
 {
     MA s;
     s.init();
     while(y)
     {
         if(y&) s = mul(s, x);
         x = mul(x, x);
         y >>= ;
     }
     return s;
 }

 int main()
 {
     LL n, a0, ax, ay, b0, bx, by;
     while(scanf("%lld",&n)!=EOF)
     {
         scanf("%lld%lld%lld", &a0,&ax,&ay);
         scanf("%lld%lld%lld", &b0,&bx,&by);
         a0 %= MOD; ax %= MOD; ay %= MOD;
         b0 %= MOD; bx %= MOD; by %= MOD;

         if(n==)
         {
             printf("%lld\n", 0LL);
             continue;
         }

         MA s;
         memset(s.mat, , sizeof(s.mat));
         s.mat[][] = ;
         s.mat[][] = s.mat[][] = 1LL*ax*bx%MOD;
         s.mat[][] = s.mat[][] = 1LL*ax*by%MOD;
         s.mat[][] = s.mat[][] = 1LL*ay*bx%MOD;
         s.mat[][] = s.mat[][] = 1LL*ay*by%MOD;
         s.mat[][] = ax; s.mat[][] = ay;
         s.mat[][] = bx; s.mat[][] = by;
         s.mat[][] = ;

         LL f0, s0;
         s0 = f0 = 1LL*a0*b0%MOD;
         s = qpow(s, n-);
         LL ans = ;
         ans += (1LL*s0*s.mat[][]%MOD+1LL*f0*s.mat[][]%MOD)%MOD, ans %= MOD;
         ans += (1LL*a0*s.mat[][]%MOD+1LL*b0*s.mat[][]%MOD)%MOD, ans %= MOD;
         ans += 1LL*s.mat[][]%MOD, ans %= MOD;
         printf("%lld\n", ans);
     }
 }