WPF-3D圆柱体透视

3D圆柱体透视效果

总效果

原理：

3D面+面在摄像机方向上的2D投影点的集合

3D面效果：

2D线:

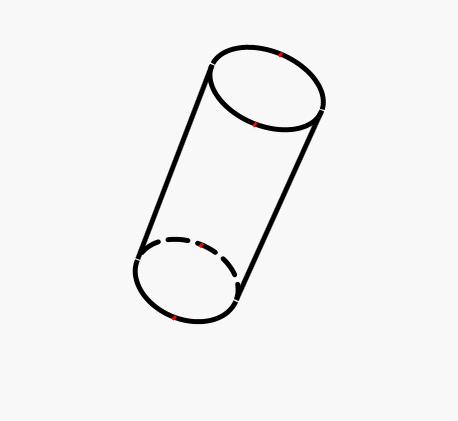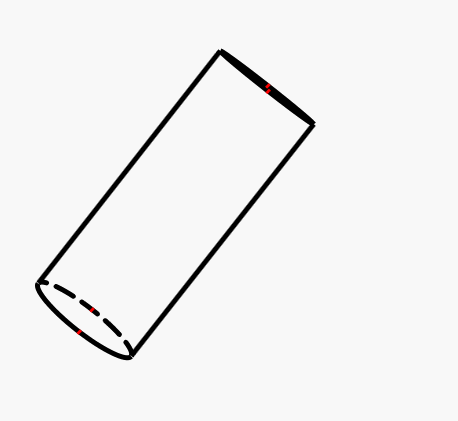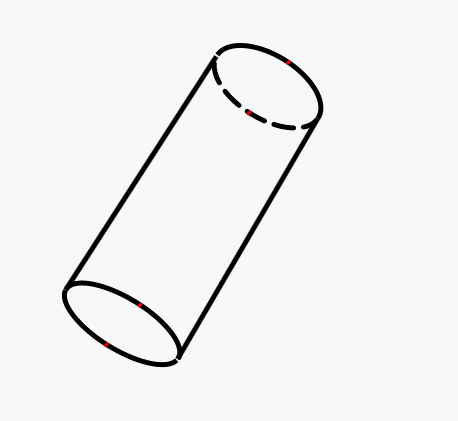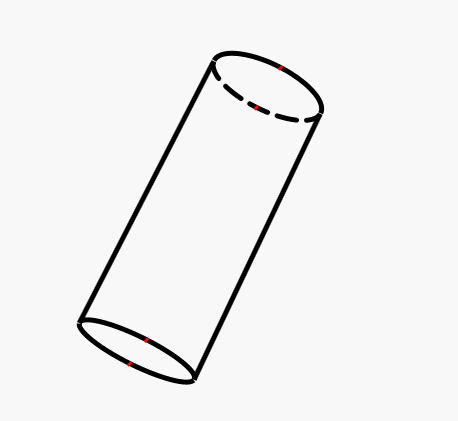
画线时需要注意两个点：

1 在圆柱体上下两个圆之间有两条竖着的棱边代表圆柱体边缘

2 被遮盖的圆面后半面显示为虚线

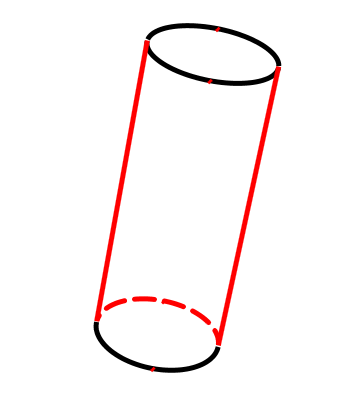
1 如何确定两条棱边的位置

我们需要确定上下两个圆面最左边和最右边的点。

随着摄像机的移动，上面的左右两个点和下面的左右两个点也随之变化

点的变化和Y轴无关，所以我们可以把它看作是个2维关系。

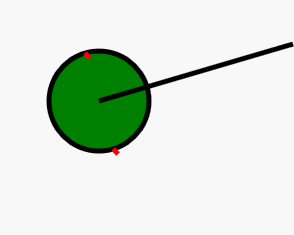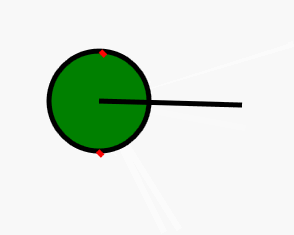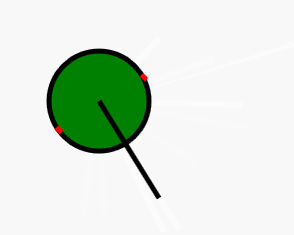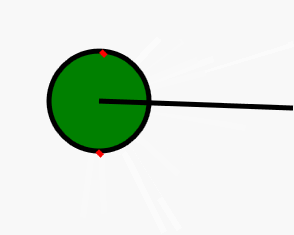
其中直线是摄像机位置视角与面中心的连线，两个红点则是这个面最左边的点和最右边的点。

即问题转变为：求一条过圆心的点直线的垂线与圆的交点。

即：

			Point3D cameraRealPosition = transform.Transform(carema.Position);
            Point caremaRealPoint = new Point(cameraRealPosition.X, cameraRealPosition.Z);
            var l1 = caremaRealPoint.X - center.X;
            var l2 = caremaRealPoint.Y - center.Y;
            var l3 = Math.Sqrt(l1 * l1 + l2 * l2);
            var sinb = l2 / l3;
            var cosb = l1 / l3;
            var x1 = r * sinb + center.X;
            var y1 = -r * cosb + center.Y;
            var x2 = -r * sinb + center.X;
            var y2 = r * cosb + center.Y;

此时我们求出一个面的点(x1,y1)(x2,y2)

在三维中，y是z轴，则点为

    		    new Point3D(x1, pointTopCenter.Y, y1)
                new Point3D(x2, pointTopCenter.Y, y2)
                new Point3D(x1, pointBottomCenter.Y, y1)
                new Point3D(x2, pointBottomCenter.Y, y2)

上下点连线则为圆柱体的侧边。

2 如何确定虚线位置。

2.1分离实线点和虚线点

我们可以发现虚线与实线是以(x1,y1)(x2,y2)分离的。

由于线是以投影点的集合组合而成。

我们可以根据每个点在(x1,y1)-(x2,y2)这条直线的左边还是右边把这个集合分成两部分。

根据向量叉乘来判断在左边还是右边。

 bool IsPointOnLineLeftOrRight(Point a, Point b, Point p)
        {
            Vector pa = new Vector(a.X - p.X, a.Y - p.Y);
            Vector pb = new Vector(b.X - p.X, b.Y - p.Y);
            return Vector.CrossProduct(pa, pb) < 0;
        }

其中ab为分别为x1y1左边两个点。

2.2确定上面存在虚线还是下面存在虚线

思路:从四个集合中选取位置相同四个点，通过和摄像机的距离比较来判断哪个集合是虚线集合

1 通过上下面相同位置的点F1,F2的距离，判断是上面存在被遮盖的面还是下面存在被遮盖的面。

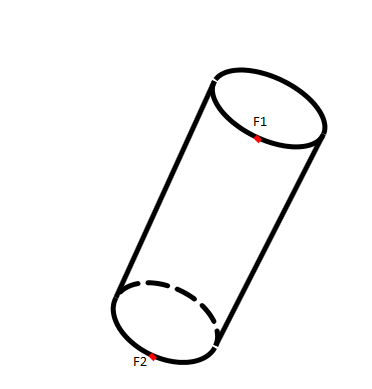
如图:

DistanceF2ToCamera>DistanceF1ToCamera

则虚线应该在下边这个圆上。

2.3 确定面左边集合是虚线还是右边集合

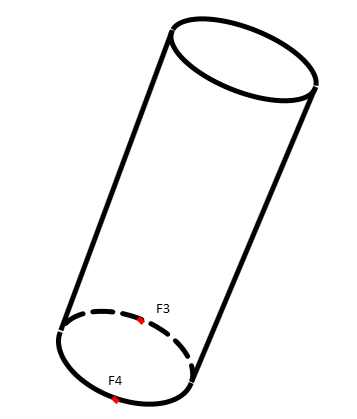
同样DistanceF3ToCamera>DistanceF4ToCamera

所以F3所在的集合是虚线点集

由此就可以判断虚线点集了。

3 点集的顺序一致性。

我们画的是开放的半圆，在画2D半圆线的时候，我们需要保证从左边第一个点开始画，画到最右边的点，

如果是从中间开始画，那么就会是个封闭的半圆了。

开放的半圆：

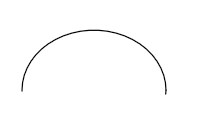
封闭的半圆：

所以我们要保证点集的顺序是从左到右的：

正常视角:

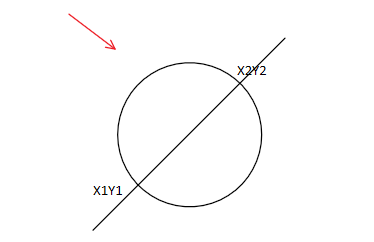
那我们存在两种情况：

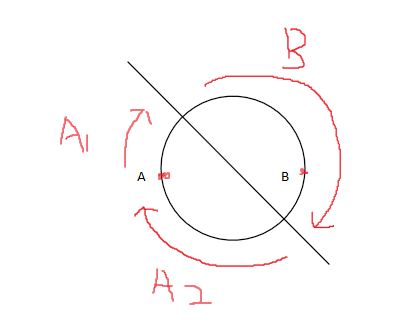
若以A为起点，则按顺序有三个点集:A1,B,A2

则

点集A=A2+A1

点集B=B

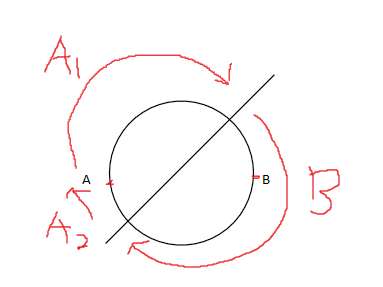
若以A为起点，则按顺序有三个点集:A1,B,A2

则

点集A=A2+A1

点集B=B

两种情况统一：

我们需要注意的是A=A2+A1

两个集合添加的时候顺序要变一下。