ansj构造最短路径
一、前言
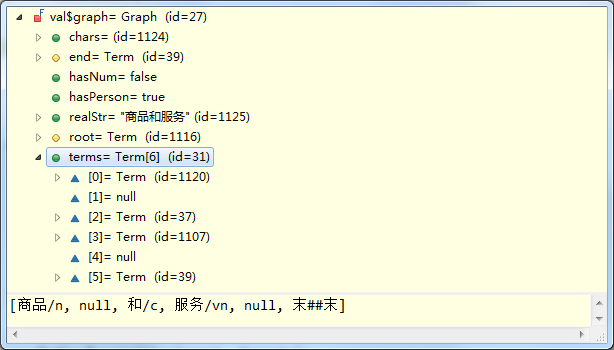
String str = "商品和服务" ;
Result result = ToAnalysis.parse(str);
System.out.println(result.getTerms());
graph.walkPath();
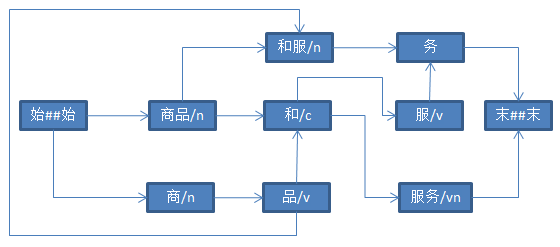

char c = chars[to];
TermNatures tn = DATDictionary.getItem(c).termNatures;
if (tn == null || tn == TermNatures.NULL) {
tn = TermNatures.NULL;
}
terms[to] = new Term(String.valueOf(c), to, tn);
二、理论基础
double value = -Math.log(dSmoothingPara * frequency / (MAX_FREQUENCE + 80000) + (1 - dSmoothingPara) * ((1 - dTemp) * nTwoWordsFreq / frequency + dTemp));
\begin{aligned}
- \log P(w_{i} | w_{i-1}) & \approx - \log \left[ aP(w_{i-1}) + (1-a) P(w_{i}|w_{i-1}) \right] \\
& \approx - \log \left[ a\frac{f(w_i)}{N} + (1-a) \left( \frac{(1-\lambda)f(w_{i-1},w_i)}{f(w_{i-1})} + \lambda \right) \right]
\end{aligned}
三、具体打分流程如下
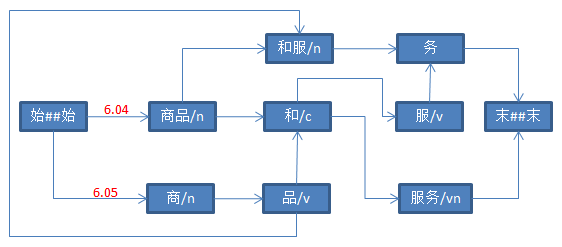
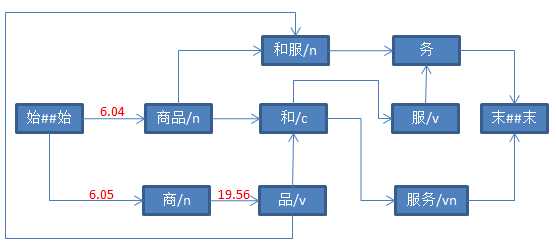
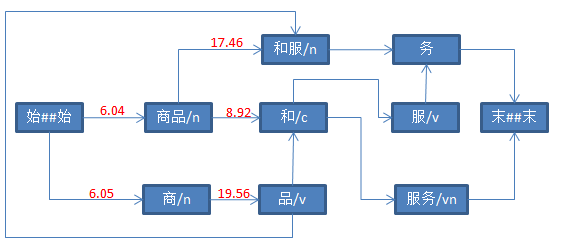
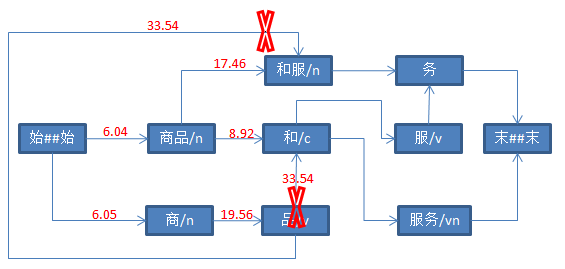
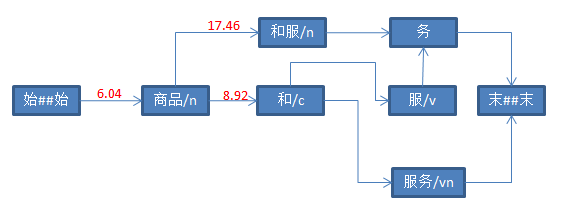
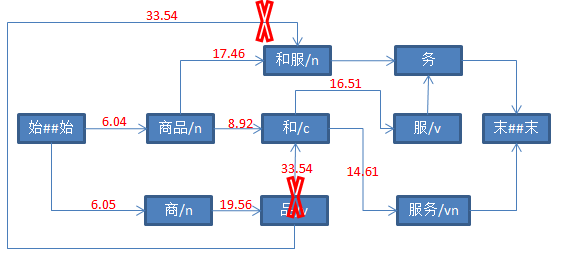
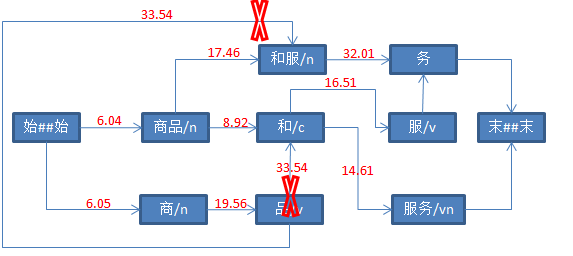
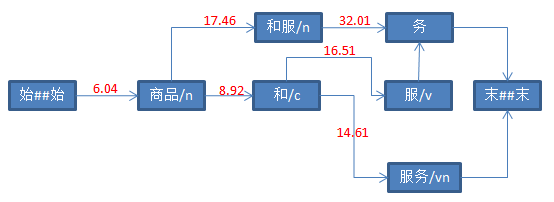

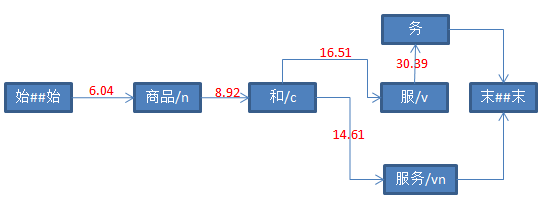

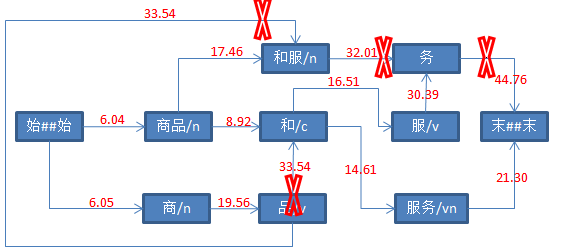
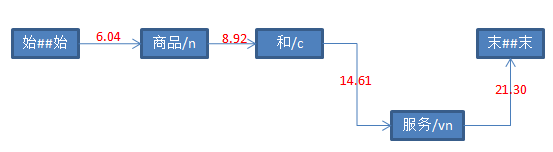
参考资料
ansj构造最短路径的更多相关文章
- ansj人名识别
1.前言 ansj人名识别会用到两个字典,分别是:person/asian_name_freq.data.person/person.dic. 1.1.asian_name_freq.data 这是一 ...
- 关于Floyd-Warshall算法由前趋矩阵计算出的最短路径反映出了算法的执行过程特性的证明
引言:Floyd-Warshall算法作为经典的动态规划算法,能够在O(n3)复杂度之内计算出所有点对之间的最短路径,且由于其常数较小,对于中等规模数据运行效率依然可观.算法共使用n此迭代,n为顶点个 ...
- 最短路径树:Dijstra算法
一.背景 全文根据<算法-第四版>,Dijkstra算法.我们把问题抽象为2步:1.数据结构抽象 2.实现 二.算法分析 2.1 数据结构 顶点+边->图.注意:Dijkstra ...
- cocos2d-js版本A*算法
[转]http://blog.csdn.net/realcrazysun1/article/details/43054229 A*算法的东西网上讲了很多~但还是不可避免的要去研究一下,cocos官网上 ...
- OSPF详解
OSPF 详解 (1) [此博文包含图片] (2013-02-04 18:02:33) 转载 ▼ 标签: 端的 第二 以太 第一个 正在 目录 序言 初学乍练 循序渐进学习OSPF 朱皓 入门之前 了 ...
- 树链剖分-点的分治(点数为k且距离最长的点对)
hdu4871 Shortest-path tree Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 130712/130712 K ( ...
- LeetCode--064--最小路径和
给定一个包含非负整数的 m x n 网格,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小. 说明:每次只能向下或者向右移动一步. 示例: 输入:[ [1,3,1], [1,5,1], ...
- Dijkstra算法构造单源点最短路径
迪杰斯特拉(Dijkstra)算法 是求从某个源点到其余各顶点的最短路径,即对已知图 G=(V,E),给定源顶点 s∈V,找出 s 到图中其它各顶点的最短路径. 我总结下核心算法,伪代码如下: Dij ...
- BZOJ 4016 最短路径树问题 最短路径树构造+点分治
题目: BZOJ4016最短路径树问题 分析: 大家都说这是一道强行拼出来的题,属于是两种算法的模板题. 我们用dijkstra算法算出1为源点的最短路数组,然后遍历一下建出最短路树. 之后就是裸的点 ...
随机推荐
- Android 几种网络请求的区别与联系
HttpUrlConnection 最开始学android的时候用的网络请求是HttpUrlConnection,当时很多东西还不知道,但是在android 2.2及以下版本中HttpUrlConne ...
- ssh命令大全
常用格式:ssh [-l login_name] [-p port] [user@]hostname 更详细的可以用ssh -h查看. 举例 不指定用户: ssh 192.168.0.11 指定用户: ...
- DB Query Analyzer 6.03, the most excellent Universal DB Access tools on any Microsoft Windows OS
DB Query Analyzer 6.03, the most excellent Universal database Access tools on any Microsoft Wind ...
- 网站开发进阶(十)如何将一个html页面嵌套在另一个页面中
如何将一个html页面嵌套在另一个页面中 1.IFrame引入 <IFRAME NAME="content_frame" width=100% height=30 margi ...
- 在Windows使用git工具将代码同步至github(作者:ying1989920)
[ps]git是一个分布式代码管理工具,类似于svn,方便协同开发,git里面有所谓的仓库(用来存放代码的),分为本地和线上,线上的你可以自己搭建,不想搭建的话github就给你提供了. [关于 ...
- OpenCV——色调映射
// define head function #ifndef PS_ALGORITHM_H_INCLUDED #define PS_ALGORITHM_H_INCLUDED #include < ...
- unity C#更改系统默认鼠标指针
最近项目需要替换鼠标的默认图标,实现的效果是初始状态为一种图标,点击鼠标左键要换成另一种图标,按网上通用的方法做了以后,隐藏鼠标指针,在指针的位置画一个图片就可以了,但不知道怎么回事,这种方法画的图标 ...
- javascript语言扩展:可迭代对象(1)
在ECMAScript中我们知道可以通过for in语句进行对象属性的遍历,当然这些属性不包括继承而来的属性: var ary = [1,2,3,"aa",4]; for(i in ...
- 【基础】CSS实现多重边框的5种方式
简言 目前最优雅地实现多重边框的方案是利用CSS3 的 box-shadow属性,但如果要兼容老的浏览器,则需要选择其它的方案.本文简要地列举了几种多重边框的实现方案,大家可以根据项目实际及兼容性要求 ...
- Pascal's Triangle(杨辉三角)
Given numRows, generate the first numRows of Pascal's triangle. For example, given numRows = 5,Retur ...
