P4178 Tree（点分治）

题面要求小于等于K的路径数目，我么很自然的想到点分治(不会的就戳我)

这道题的统计答案与模板题不一样的地方是由等于K到小于等于K

那么我们可以把每一个子节点到当前根（重心）的距离排序，然后用类似双指针的方法来求小于等于K的边的数量

但是如果只是双指针统计的话，那么以下不合法的情况显然也会被算进答案：

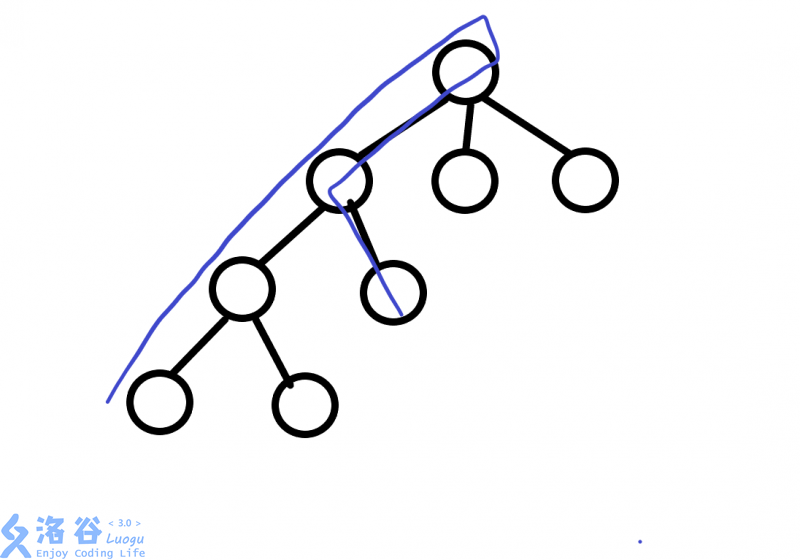
而我们需要的合法路径是长成这样的：

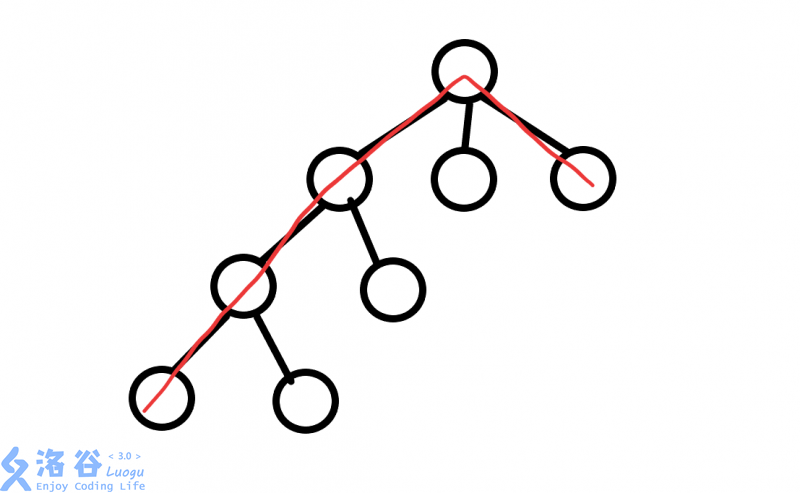
所以我们需要减去上述不合法的路径，怎么减呢？

不难发现，对于所有不合法的路径，都是在当前跟的某一棵子树上的（没有跨越两个子树）

所以我们可以对当前跟节点的每一条边进行遍历，利用容斥的思想减去不合法的路径。

具体操作为：当遍历重心节点的每一个节点时，我们可以重新计算dis，然后把经过了从重心到新遍历的点的边两次的路径剪掉（就是上述不合法路径），最后统计答案即可

#include<bits/stdc++.h>
using namespace std;
#define il inline
#define re register
#define inf 123456789
il int read()
{
    re int x = 0, f = 1; re char c = getchar();
    while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
    return x * f;
}
#define rep(i, s, t) for(re int i = s; i <= t; ++ i)
#define drep(i, s, t) for(re int i = t; i >= s; -- i)
#define Next(i, u) for(re int i = head[u]; i; i = e[i].next)
#define mem(k, p) memset(k, p, sizeof(k))
#define maxn 40005
struct edge{int v, w, next;}e[maxn << 1];
int n, m, head[maxn], cnt, k, ans;
int dp[maxn], vis[maxn], sum, dis[maxn], rt, size[maxn], rev[maxn], tot;
il void add(int u, int v, int w)
{
    e[++ cnt] = (edge){v, w, head[u]}, head[u] = cnt;
    e[++ cnt] = (edge){u, w, head[v]}, head[v] = cnt;
}
il void getrt(int u, int fr)
{
    size[u] = 1, dp[u] = 0;
    Next(i, u)
    {
        int v = e[i].v;
        if(v == fr || vis[v]) continue;
        getrt(v, u);
        size[u] += size[v], dp[u] = max(dp[u], size[v]);
    }
    dp[u] = max(dp[u], sum - size[u]);
    if(dp[u] < dp[rt]) rt = u;
}
il void getdis(int u, int fr)
{
    rev[++ tot] = dis[u];
    Next(i, u)
    {
        int v = e[i].v;
        if(v == fr || vis[v]) continue;
        dis[v] = dis[u] + e[i].w;
        getdis(v, u);
    }
}
il int doit(int u, int w)
{
    tot = 0, dis[u] = w, getdis(u, 0);
    sort(rev + 1, rev + tot + 1);
    int l = 1, r = tot, ans = 0;
    while(l <= r) (rev[l] + rev[r] <= k) ? (ans += r - l, ++ l) : (-- r);
    return ans;
}
il void solve(int u)
{
    vis[u] = 1, ans += doit(u, 0);
    Next(i, u)
    {
        int v = e[i].v;
        if(vis[v]) continue;
        ans -= doit(v, e[i].w);
        sum = size[v], dp[0] = n, rt = 0;
        getrt(v, u), solve(rt);
    }
}
int main()
{
    n = read();
    rep(i, 1, n - 1){int u = read(), v = read(), w = read(); add(u, v, w);}
    k = read(), dp[0] = sum = n, getrt(1, 0), solve(rt);
    printf("%d", ans);
    return 0;
}