[IOI 2011]ricehub

Description

乡间有一条笔直而长的路称为“米道”。沿着这条米道上 R 块稻田，每块稻田的坐标均
为一个 1 到 L 之间(含 1 和 L)的整数。这些稻田按照坐标以不减的顺序给出，即对于 0 ≤ i <
R，稻田 i 的坐标 X[i]满足 1 ≤ X[0] ≤ ... ≤ X[R-1] ≤ L。 
注意：可能有多块稻田位于同一个坐标上。 
我们计划建造一个米仓用于储存尽可能多的稻米。和稻田一样，米仓将建在米道上，其
坐标也是一个 1 到 L 之间的整数（含 1 和 L）。这个米仓可以建在满足上述条件的任一个位
置上，包括那些原来已有一个或多个稻田存在的位置。 
在收获季节，每一块稻田刚好出产一滿货车的稻米。为了将这些稻米运到米仓，需要雇
用一位货车司机来运米。司机的收费是每一满货车运送一个单位的距离收取 1 元。換言之，
将稻米从特定的稻田运到米仓的费用在数值上等于稻田坐标与米仓坐标之差的绝对值。 
不幸的是，今年预算有限，我们至多只能花费 B 元运费。你的任务是要帮我们找出一个
建造米仓的位置，可以收集到尽可能多的稻米。

Input

第一行 三个整数 R L B
接下来R行 每行一个整数 表示X[i]

Output

一个整数 最多稻米数

Sample Input

5 20 6
1
2
10
12
14

Sample Output

3

HINT

1 ≤ R ≤ 100,000
1 ≤ L ≤ 1,000,000,000
0 ≤ B ≤ 2,000,000,000,000,000

题解

做的第二道$IOI$的题，虽然还是水题。NOIp小孩都会做。

我们考虑二分答案，对于每个二分的答案$mid$，其实其另外一个性质就是它是在数轴上包含$mid$个点的区间。

现在我们的问题就是这$mid$个点的区间中各个点到某一位置的最小值是否$<=B$。

一个有价值的性质就是：数轴上$n$个点，若$n$为奇，那么所有点到点$\lceil {n \over 2} \rceil$的总距离是最短的，而若$n$为偶，那么到$n \over 2$或${n \over 2}+1$的距离相等且最短。

那么我们现在显然就是在数轴上找出所有包含$mid$个点的区间，并计算其最小距离和是否$<=B$。

统计总距离：对于检查的$r$，我们再取$mid = {r \over 2}$。

随着$pos-1$（中点）向右移到$pos$，我们统计的值满足下列变换：

     tot -= abs(a[pos-(r&)]-a[pos-(r&)-mid]);
     tot += abs(a[pos+mid]-a[pos]);

附张图片便于理解上式：

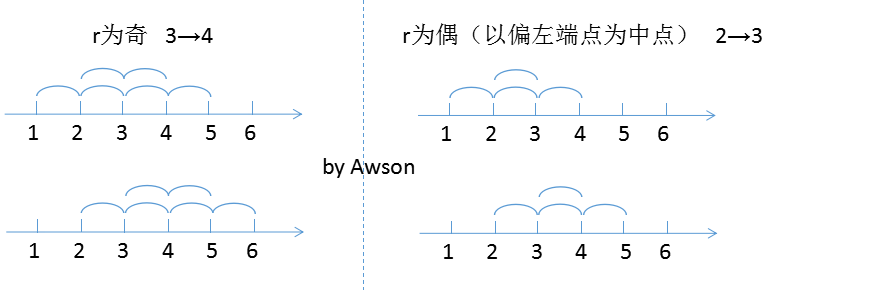
 //It is made by Awson on 2017.10.17
 #include <set>
 #include <map>
 #include <cmath>
 #include <ctime>
 #include <stack>
 #include <queue>
 #include <vector>
 #include <string>
 #include <cstdio>
 #include <cstdlib>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 #define LL long long
 #define Min(a, b) ((a) < (b) ? (a) : (b))
 #define Max(a, b) ((a) > (b) ? (a) : (b))
 #define Abs(x) ((x) < 0 ? (-(x)) : (x))
 using namespace std;
 const int N = ;

 LL n, m, b;
 LL a[N+];

 bool check(LL r) {
     LL mid = r>>, pos = mid+(r&), tot = ;
     for (int i = ; i <= r; i++) tot += Abs(a[i]-a[pos]);
     if (tot <= b) return true;
     for (pos++; pos+mid <= n; pos++) {
         tot -= Abs(a[pos-(r&)]-a[pos-(r&)-mid]);
         tot += Abs(a[pos+mid]-a[pos]);
         if (tot <= b) return true;
     }
     return false;
 }
 void work() {
     scanf("%lld%lld%lld", &n, &m, &b);
     for (int i = ; i <= n; i++) scanf("%lld", &a[i]);
     LL L = , R = n, ans = ;
     while (L <= R) {
         LL mid = (L+R)>>;
         if (check(mid)) ans = mid, L = mid+;
         else R = mid-;
     }
     printf("%lld\n", ans);
 }
 int main() {
     work();
     return ;
 }