2010 NEERC Western subregional

Problem A. Area and Circumference

题目描述：给定平面上的$n$个矩形，求出面积与周长比的最大值。

solution
枚举。

时间复杂度：$O(n)$

Problem C. Canonical Binary Tree

题目描述：有$n$个点，每次拿出$2^x<=n$个点（$x$取最大）构成一棵满二叉树，将构成的树依次从左到右排列，然后从右到左依次合并最小的两棵树，构成一棵更大的二叉树。那么每个数可以用从根出发的一条路径表示，即一个$LR$序列（从根出发每次选择左儿子还是右儿子），现在有若干个询问，若询问给出的是点的编号，则输出其路径表示，如果询问给出的是路径表示，则输出对应的编号。

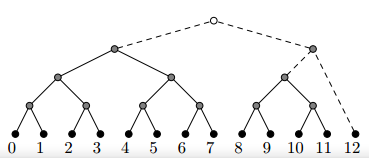
solution
$n$的二进制有多少个$1$就有多少棵树，而且每个$1$对应的位置就是对应的树的叶子节点数，按照这个很容易就能解决问题。

时间复杂度：$O(logn)$

Problem D. Domino

题目描述：给出$n$个无序数对，$m$个排列好的数字，现在可以选择一个数对排在排列的前面或后面，能排在前面（后面）当且仅当数对中的一个数字与最前面（后面）的数字相同，或者可以选择两个数对,一个放在前面，一个后面，但这两个数对都要是数字相同的数对。问剩下的数对的和的最小值。

solution
枚举。

时间复杂度：$O(n^2)$

Problem E. Express Lines

题目描述：在一个有$n$个点的环上选择不少于$2$个点，而且选择的点不相邻的方案数。

solution
$dp$，把环拆成链，$f[i][0$~$1][0$~$1]$表示到第$i$个点，开头的点有没有选，第$i$个点有没有选的方案。答案等于$f[n][0][0]+f[n][0][1]+f[n][1][0]$

时间复杂度：$O(n)$

Problem F. Filter-Art

题目描述：有一个$n \times m$的网格图，每个格子一开始是零，可以在网格中选择若干个边长相等的正方形，选择的第一个正方形里面的数加$1$，第二个加$2$，以此类推，但选择的每个正方形至少有一个网格没有被其它选择的正方形覆盖。现在给出最后的网格图，求对应的一种方案。

solution
枚举边长，由于每个正方形至少有一个网格没有被其它选择的正方形覆盖，因此每次找到最上最左的不为零的格子，这个格子的数就是对应的正方形编号，然后将这个正方形减掉，最终整个网格图都为零则找到一个解。这里减掉一个正方形可以用二维前缀和来维护。

时间复杂度：$O(n^3)$

Problem G. Game

题目描述：有$m$个球，每个球上有两个按钮，一个对应蓝色，一个对应红色，但不知道哪个按钮对应哪种颜色。现在以放回的方式依次取出两个球，记录按下的按钮对应的颜色，如果两个球选择的颜色相同，则赢，否则输。现在知道其中一个取出的球的编号不超过$k$，且这个球选择的颜色是蓝色，问赢的概率。

solution
条件概率，乘法公式。设事件$A$为赢，$B$为其中一个取出的球的编号不超过$k$且这个球选择的颜色是蓝色。
\[P(A|B)=\frac{P(AB)}{P(B)}=\frac{2(k)(m)-k^2}{2(k)(2m)-k^2}=\frac{2m-k}{4m-k}\]

时间复杂度：$O(1)$

Problem I. "Injurious" Triples

题目描述：在一个序列里面找出一个三个数的子序列满足这三个数按原顺序构成等差数列。

solution
暴力枚举两个数，判断另一个数是否存在。

时间复杂度：$O(n^2)$

Problem M. Munich

题目描述：有三种日票，第一种是成人票，价格为$p_1$，第二种是儿童票，价格为$p_2$，但儿童也可以买成人票，第三种是团体票，最多可以有$5$个成人，一个成人可以换成$1$个或$2$个儿童，价格为$p_3$。还有三种三日票，跟普通日票一样，只是能用三日而已。现在有$m$个成人，$n$个儿童来玩$k(1\leq k \leq 3)$天，问最少花费多少钱买票。

solution
$dp$。$f[i][j]$表示$i$个成人，$j$个儿童已经买了票的最少花费，然后按题意转移就好。

时间复杂度：$O(n^2)$