机器学习基石9-Linear Regression

注：
文章中所有的图片均来自台湾大学林轩田《机器学习基石》课程。
笔记原作者：红色石头
微信公众号：AI有道

上节课，主要介绍了在有noise的情况下，VC Bound理论仍然是成立的。同时，介绍了不同的error measure方法。本节课介绍机器学习最常见的一种算法：Linear Regression.

一、线性回归问题

在之前的Linear Classification课程中，讲了信用卡发放的例子，利用机器学习来决定是否给用户发放信用卡。本节课仍然引入信用卡的例子，来解决给用户发放信用卡额度的问题，这就是一个线性回归（Linear Regression）问题。

令用户特征集为\(d\)维的，加上常数项，维度为\(d+1\)，与权重\(w\)的线性组合即为Hypothesis，记为\(h(x)\)。线性回归的预测函数取值在整个实数空间，这是与线性分类不同的点。

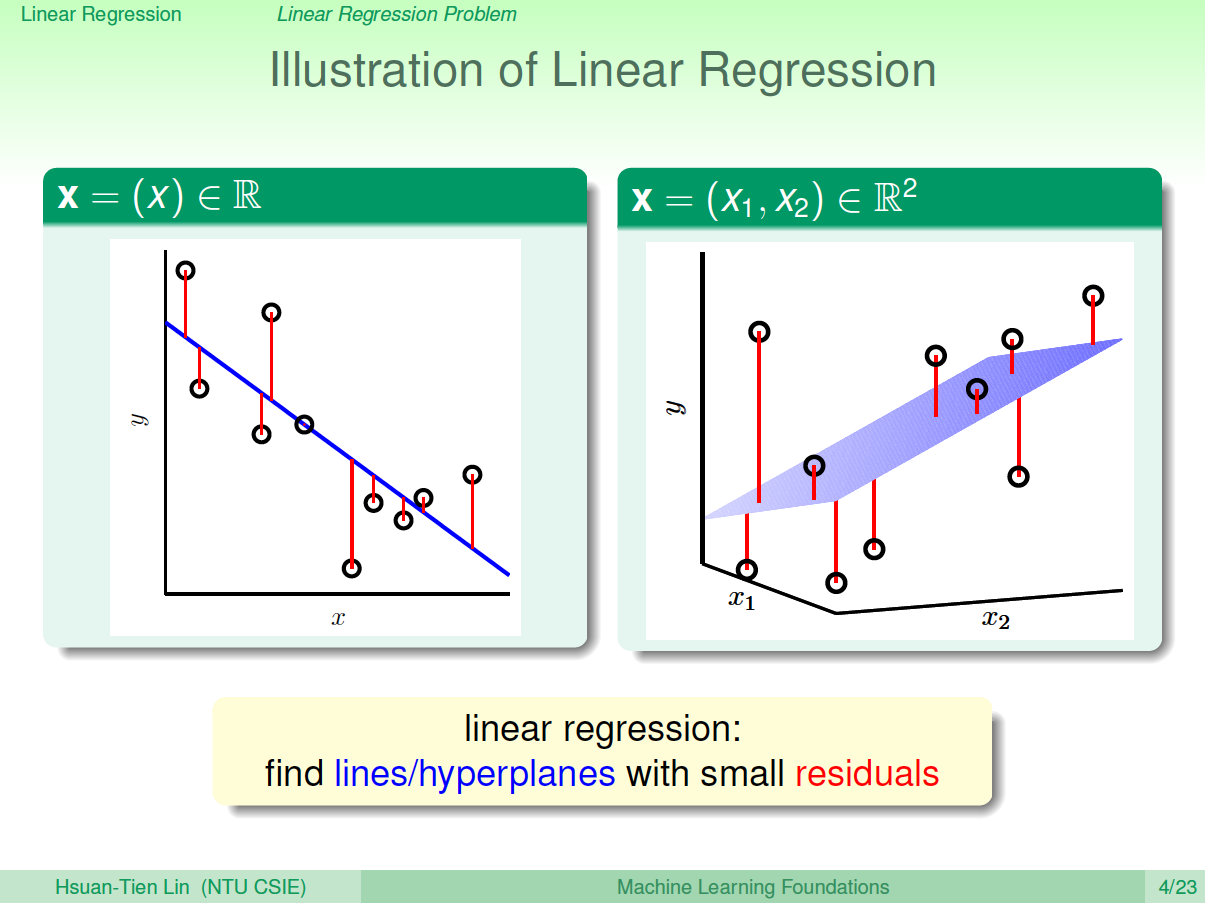
根据上图，在一维或者多维空间里，线性回归的目标是找到一条直线（对应一维）、一个平面（对应二维）或者更高维的超平面，使样本集中的点更接近它，也就是残留误差Residuals最小化。

一般最常用的误差衡量方式是基于最小二乘法，其目标是计算误差的最小平方和对应的权重\(w\)，即上节课介绍的squared error：

最小二乘法可以解决线性问题和非线性问题。线性最小二乘法的解是closed form，即\(X=(A^TA)^{-1}A^Ty\)，而非线性最小二乘法没有closed form，通常用迭代法求解。本节课的解是closed form的。

二、线性回归算法

样本数据误差\(E_{in}\)是权重\(w\)的函数，因为\(X\)和\(y\)都是已知的。我们的目标就是找出合适的\(w\)，使\(E_{in}\)能够最小。那么如何计算呢？

首先，运用矩阵转换的思想，将计算转换为矩阵的形式。

对于此类线性回归问题， \(E_{in}(w)\)一般是个凸函数。对于凸函数，我们只要找到一阶导数等于零的位置，就找到了最优解。那么，我们将\(E_{in}(w)\)对每个\(w_i,i=0,1,...,d\)求偏导，偏导为零的\(w_i\)，即为最优化的权重值分布。

根据梯度的思想，对\(E_{in}(w)\)进行矩阵化求偏导处理：

令偏导为零，最终可以计算出权重向量为：

最终，我们推导得到了权重向量\(w=(X^TX)^{-1}X^Ty\)，这是上文提到的closed form解。其中， \((X^TX)^{-1}X^T\)又称为伪逆矩阵pseudo-inverse，记为\(X^{\dagger}\)，维度是\((d+1)\times N\)。
但是，注意到，伪逆矩阵中有逆矩阵的计算，逆矩阵\((X^TX)^{-1}\)是否一定存在？一般情况下，只要满足样本数量\(N\)远大于样本特征维度\(d+1\)，就能保证矩阵的逆是存在的，称之为非奇异矩阵。但是如果是奇异矩阵，不可逆怎么办呢？其实，大部分的计算逆矩阵的软件程序，都可以处理这个问题，也会计算出一个逆矩阵。所以，一般伪逆矩阵是可解的。

三、泛化问题

现在，可能有这样一个疑问，就是这种求解权重向量的方法是机器学习吗？或者说这种方法是否满足我们之前推导VC Bound，即是否拥有泛化能力\(E_{in}\approx E_{out}\)？

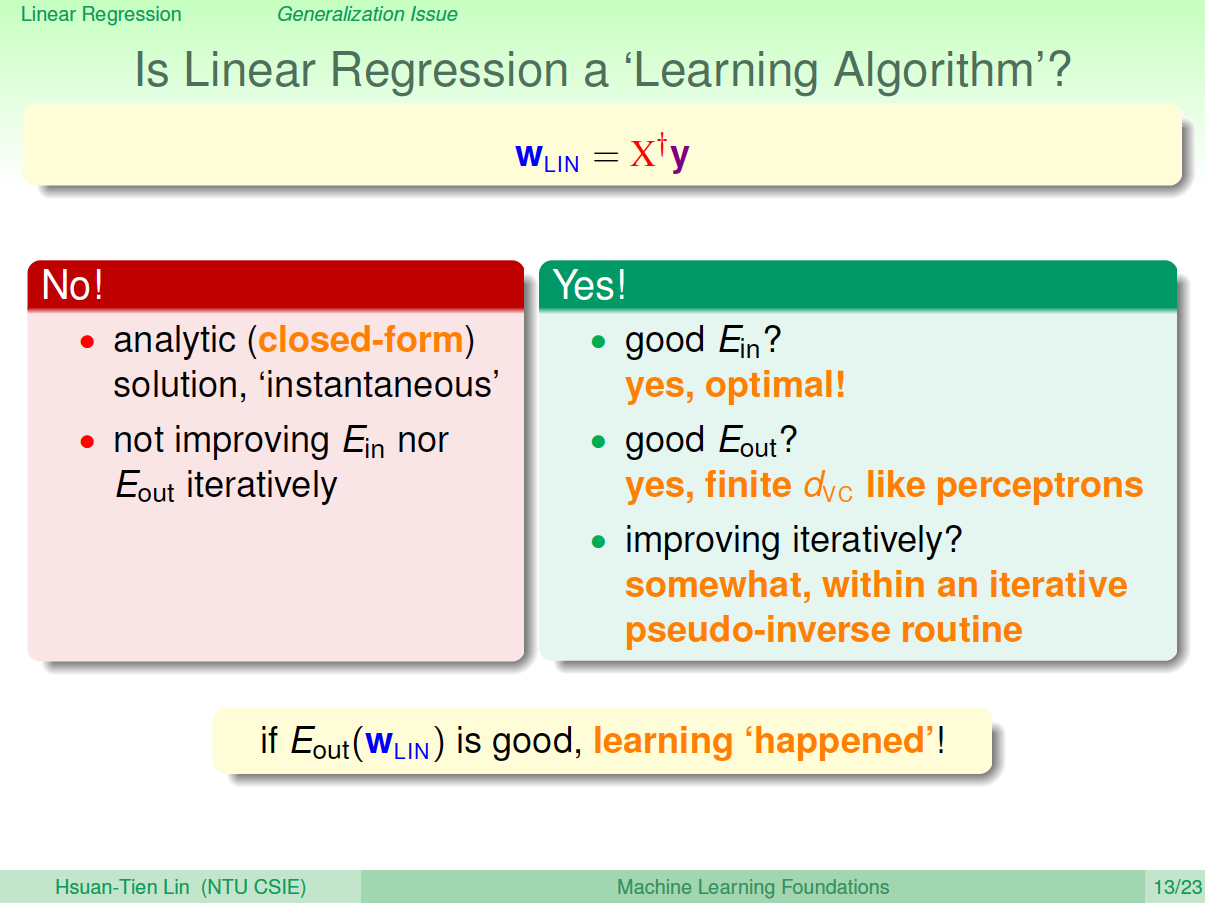
有两种观点：1、这不属于机器学习范畴。因为这种closed form解的形式跟一般的机器学习算法不一样，而且在计算最小化误差的过程中没有用到迭代。2、这属于机器学习范畴。因为从结果上看，\(E_{in}\) 和\(E_{out}\)都实现了最小化，而且实际上在计算逆矩阵的过程中，也用到了迭代。

其实，只从结果来看，这种方法的确实现了机器学习的目的。下面通过介绍一种更简单的方法，证明linear regression问题是可以通过线下最小二乘法方法计算得到好的\(E_{in}\)和\(E_{out}\)的。

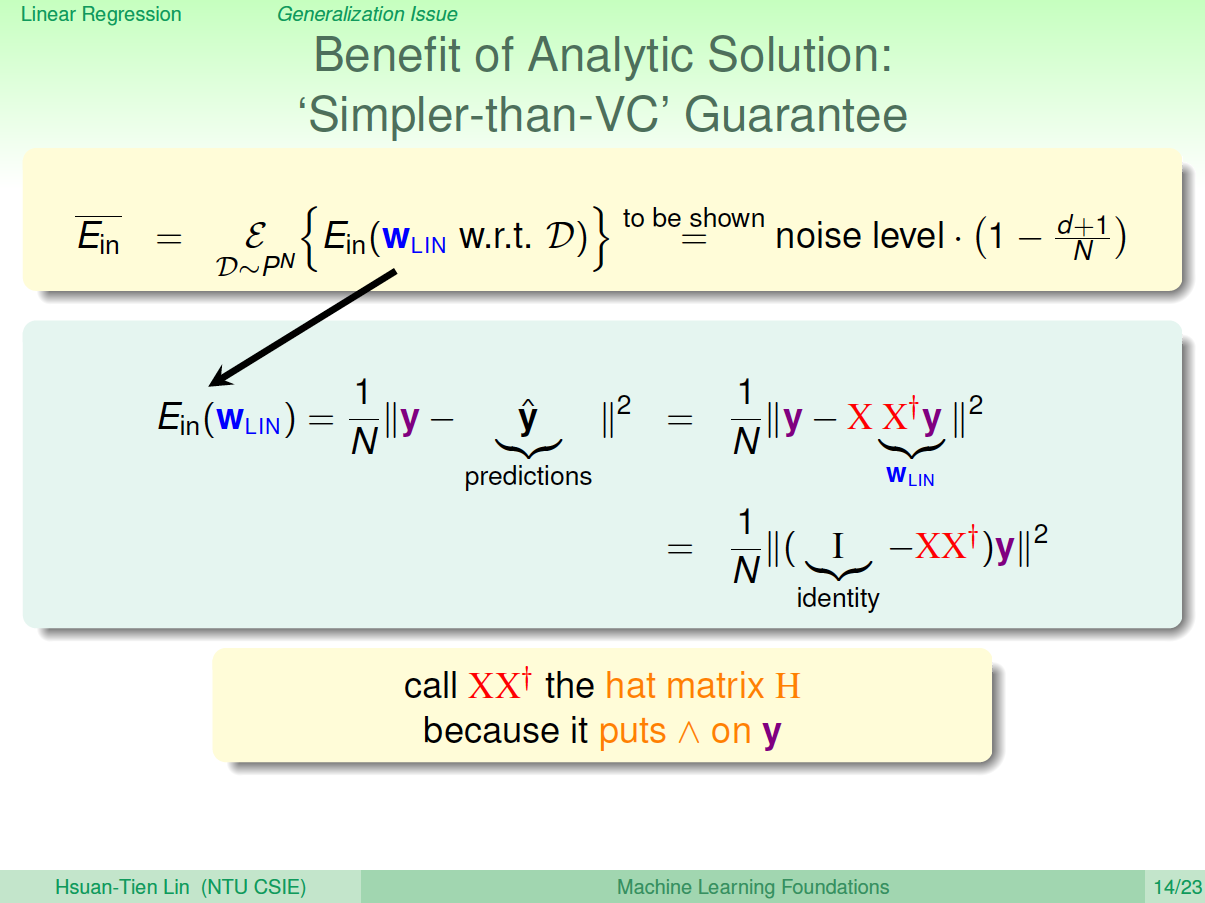
首先，我们根据平均误差的思想，把\(E_{in}(w_{LIN})\)写成如图的形式，经过变换得到:\[E_{in}(w_{LIN})=\frac{1}{N}\|(I-XX^{\dagger})y\|^2\]
称\(XX^{\dagger}\)为帽子矩阵，用\(H\)表示。
下面从几何图形的角度来介绍帽子矩阵H的物理意义。

图中，\(y\)是\(N\)维空间的一个向量，粉色区域表示输入矩阵\(X\)乘以不同权值向量\(w\)所构成的空间，根据所有\(w\)的取值，预测输出都被限定在粉色的空间中。向量\(\hat{y}\)就是粉色空间中的一个向量，代表预测的一种。\(y\)是实际样本数据输出值。

机器学习的目的是在粉色空间中找到一个\(\hat{y}\)，使它最接近真实的\({y}\)，那么我们只要将\(y\)在粉色空间上作垂直投影即可，投影得到的\(\hat{y}\)即为在粉色空间内最接近\(y\)的向量。这样就可以使得平均误差\(\bar{E}\)最小。

从图中可以看出， \(\hat{y}\)是\(y\)的投影，已知\(\hat{y}=Hy\)，那么\(H\)表示的就是将\(y\)投影到\(\hat{y}\)的一种操作。图中绿色的箭头\(y-\hat{y}\)是向量\(y\)与\(\hat{y}\)相减， \(y-\hat{y}\)垂直于粉色区域。已知\((I-H)y=y-\hat{y}\)那么\(I-H\)表示的就是将\(y\)投影到\(y-\hat{y}\)即垂直于粉色区域的一种操作。这样的话，我们就赋予了\(H\)和\(I-H\)不同但又有联系的物理意义。

图中\(trace(I-H)\)称为\(I-H\)的迹，值为\(N-(d+1)\)。这条性质很重要，一个矩阵的trace等于该矩阵的所有特征值(Eigenvalues)之和。下面给出简单证明：\[trace(I-H)=trace(I)-trace(H)=N-trace(XX^{\dagger})=N-trace(X(X^TX)^{-1}X^T)=N-trace(X^T(X^TX)^{-1})=N-trace(I_{d+1})=N-(d+1)\]
介绍下\(I-H\)这种转换的物理意义：原来有一个有\(N\)个自由度的向量\(y\)，投影到一个有\(d+1\)维的空间\(x\)（代表一列的自由度，即单一输入样本的参数，如图中粉色区域），而余数剩余的自由度最大只有\(N-(d+1)\)种。

在存在noise的情况下，上图变为：

图中，粉色空间的红色箭头是目标函数\(f(x)\)，虚线箭头是noise，可见，真实样本输出\(y\)由\(f(x)\)和noise相加得到。由上面推导，已知向量\(y\)经过\(I-H\)转换为\(y-\hat{y}\)，而noise与\(y\)是线性变换关系，根据线性函数知识，可以推导出noise经过\(I-H\)也能转换为\(y-\hat{y}\)。
则对于样本平均误差，有下列推导成立：
\[
E_{in}(w_{LIN})=\frac{1}{N}\|y-\hat{y}\|^2=\frac{1}{N}\|(I-H)noise\|^2=\frac{1}{N}(N-(d+1))\|noise\|^2
\]
即\[\bar{E}_{in}=noiselevel*(1-\frac{d+1}{N})\]
同样地，对\(E_{out}\)有如下结论：
\[\bar{E}_{out}=noiselevel*(1+\frac{d+1}{N})\]
这个证明有点复杂，但是我们可以这样理解： \(\bar{E}_{in}\)与\(\bar{E}_{out}\)形式上只差了\(\frac{d+1}{N}\)项，从哲学上来说， \(\bar{E}_{in}\)是看得到的样本的平均误差，如果有noise，我们把预测往noise那边偏一点，让\(\bar{E}_{in}\)好看一点点，所以减去\(\frac{d+1}{N}\)项。那么同时，新的样本\(\bar{E}_{out}\)是我们看不到的，如果noise在反方向，那么\(\bar{E}_{out}\)就应该加上\(\frac{d+1}{N}\)项。
把\(\bar{E}_{in}\)与\(\bar{E}_{out}\)画出来，得到学习曲线：

当\(N\)足够大时， \(\bar{E}_{in}\)与\(\bar{E}_{out}\)逐渐接近，满足\(\bar{E}_{in}\approx \bar{E}_{out}\)，且数值保持在noise level。这就类似VC理论，证明了当\(N\)足够大的时候，这种线性最小二乘法是可以进行机器学习的，算法有效！

四、Linear Regression方法解决Linear Classification问题

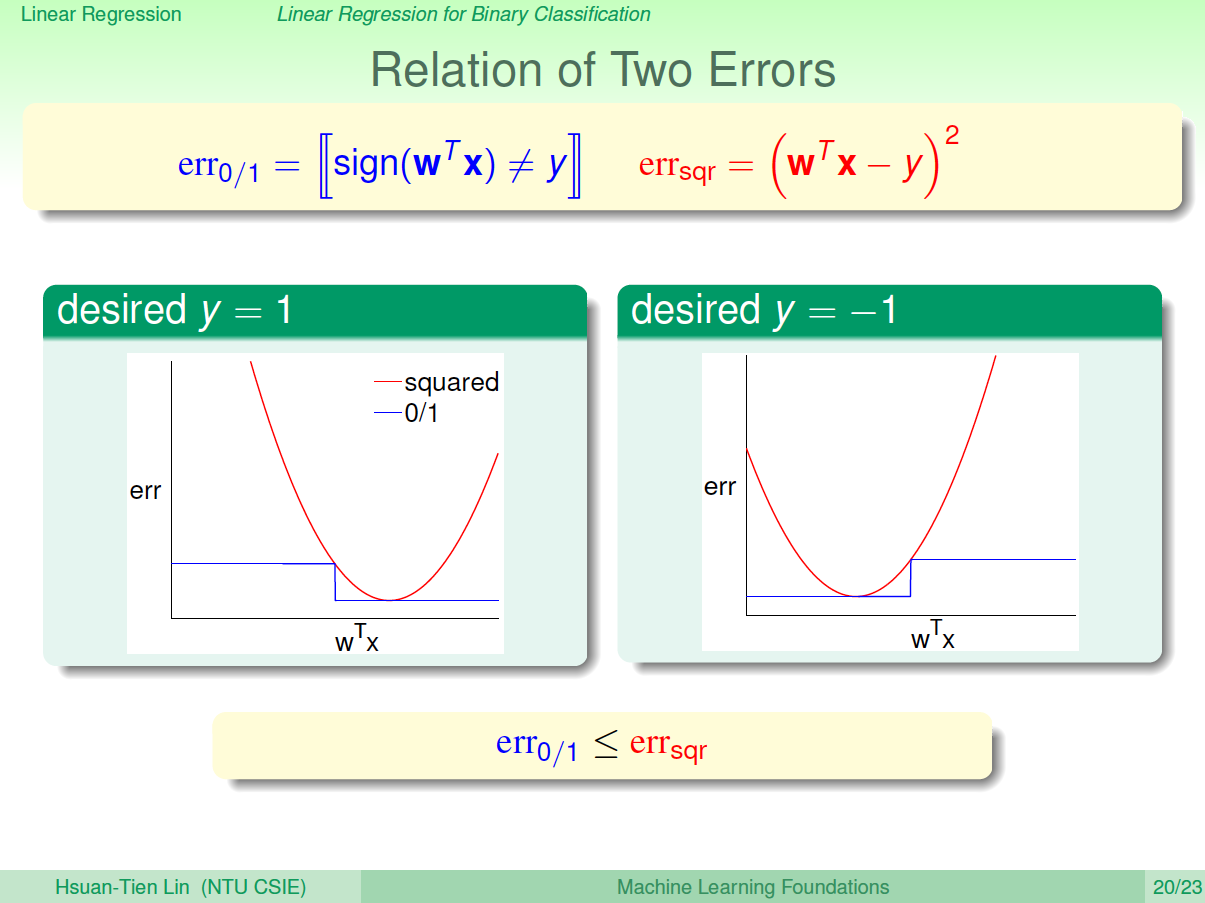
之前介绍的Linear Classification问题使用的Error Measure方法用的是0/1 error，那么Linear Regression的squared error是否能够应用到Linear Classification问题？

下图展示了两种误差的关系，一般情况下，squared error曲线在0/1 error曲线之上。即\(err_{0/1}\leq err_{sqr}\)

根据之前的VC理论，\(E_{out}\) 的上界满足：

从图中可以看出，用\(err_{sqr}\)代替\(err_{0/1}\)， \(E_{out}\)仍然有上界，只不过是上界变得宽松了。也就是说用线性回归方法仍然可以解决线性分类问题，效果不会太差。二元分类问题得到了一个更宽松的上界，但是也是一种更有效率的求解方式。

五、总结

本节课，主要介绍了Linear Regression。首先，我们从问题出发，想要找到一条直线拟合实际数据值；然后，我们利用最小二乘法，用解析形式推导了权重\(w\)的closed-form解；接着，用图形的形式得到\(E_{out}-E_{in}\approx \frac{2(d+1)}{N}\)，证明了linear regression是可以进行机器学习的；最后，我们证明linear regressin这种方法可以用在binary classification上，虽然上界变宽松了，但是仍然能得到不错的学习方法。