基于C++的成功-失败法演示

确定搜索区间的一维搜索算法

求多元函数 f(x) 的最优解通常采用迭代的方法：

1. 在可行域内任取一点 x⁰作为初始点，从 x⁰ 出发，按照一定的方法，一次找到 x¹,x²,x³,…,xⁿ,…, 使得某个xⁿ为函数 f(x) 的最优解，或者点列 x¹,x²,… 收敛到函数 f(x) 的最优解。在这个过程中，我们希望点列满足 f(x^k+1) ≤ f(x^k) ，即在点列上 f(x) 是下降的，这就是所谓的下降算法。
2. 为求函数的最小值点，通常分两步进行：首先确定函数的搜索区间；然后不断缩短搜索区间，直至区间缩短到一点为止。下面介绍第一种搜索区间的方法---成功失败法。

一．成功-失败法

设函数 f(x) 是R¹上的单峰函数，∀x₀∊R¹ ,步长 h>0。

（1）若 f(x₀) > f(x₀+h) ,则当 f(x₀+h) > f(x₀+3h) 时，步长加倍，向前推进。此时令 x₀=x₀+h , h=2h ,重新开始搜索；否则得搜索区间[a,b]=[x₀,x₀+3h]。

（2）若 f(x₀) = f(x₀+h)，则得搜索区间 [a,b] = [x₀,x₀+h]。

（3）若 f(x₀) < f(x₀+h),则缩小步长，向后转，小步后退，即令 x₀=x₀+h ，h= -h/4 ，重新开始搜索。

根据以上思想，确定搜索区间的成功-失败法计算框图如下：

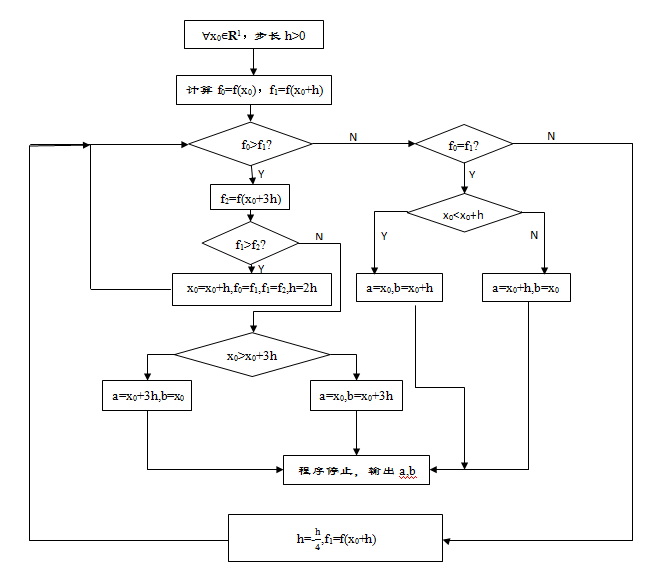
下面我们以一道例题为例说明成功-失败法在 C++ 中的实现：

例：编写成功-失败法的计算程序确定函数 f(x)=x³-27x+10 的最小值的一个搜索区间，初始点取 x₀=4.5 ，初始步长取 h=0.5 。

这里是在 Dev 编译器中实现编程的，具体代码如下：

程序运行结果如下：

以上就是成功失败法的具体样例，由于作者水平有限，希望发现不当之处的朋友及时指正，谢谢！