【P2015】二叉苹果树 (树形DP分组背包)

题目描述

有一棵苹果树，如果树枝有分叉，一定是分2叉（就是说没有只有1个儿子的结点）

这棵树共有N个结点（叶子点或者树枝分叉点），编号为1-N,树根编号一定是1。

现在这颗树枝条太多了，需要剪枝。但是一些树枝上长有苹果。

给定需要保留的树枝数量，求出最多能留住多少苹果。

输入输出格式

输入格式：

第1行2个数，N和Q(1<=Q<= N,1<N<=100)。

N表示树的结点数，Q表示要保留的树枝数量。接下来N-1行描述树枝的信息。

每行3个整数，前两个是它连接的结点的编号。第3个数是这根树枝上苹果的数量。

每根树枝上的苹果不超过30000个。

输出格式：

一个数，最多能留住的苹果的数量。

Solution

树形DP一道模板题，考虑DP

DP[ i ][ j ]表示在以i为结点的子树中保留j个边能得到的最大苹果数量

状态转移方程如下

         for(int j=min(num[cur],m);j;--j)
              for(int k=min(num[ev],j-);k>=;--k)
                DP[cur][j]=max(DP[cur][j],DP[cur][j-k-]+DP[ev][k]+e[i].w);

cur表示当前遍历到的节点，num[cur]表示以cur为节点的子树的边数(可以通过DFS预处理)

j枚举当前节点子树的保留边的个数,k表示当前边的v节点的子树的保留的边的个数,DP[cur][j]可以由保留j-k-1条边的前提下保留一个子树的k个节点转移过来。

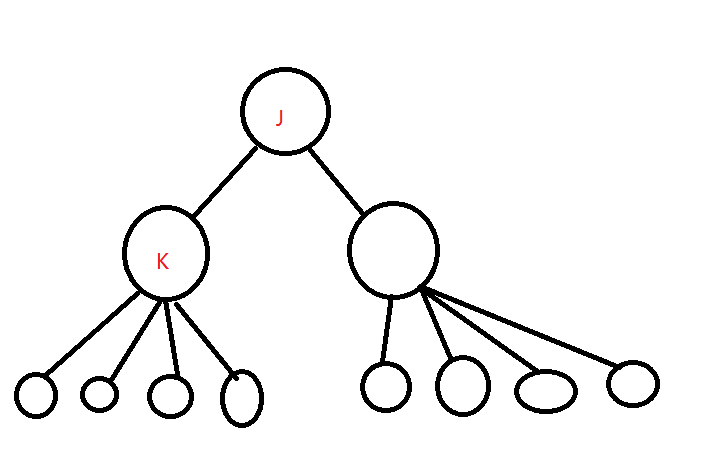
那么问题来了,如果要正确转移我们需要在处理num数组的前提下从叶节点转移，并且枚举到每条边，如何做到呢

考虑DFS的遍历顺序和树的结构是一样的，我们可以在回溯的过程中DP，这样就完美了

Code

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#define maxn 1505
#define re register
using namespace std;
int DP[maxn][maxn<<];
int cnt,ans,n,x,num[maxn],y,z,head[maxn],m;
bool vis[maxn];
struct Edge{
    int v,w,nxt;
}e[maxn<<];
void add(int u,int v,int w)
{
    e[++cnt].v=v;
    e[cnt].w=w;
    e[cnt].nxt=head[u];
    head[u]=cnt;
}
int dfs(int cur)
{
    for(int i=head[cur];i;i=e[i].nxt)
    {
        int ev=e[i].v;
        if(!vis[ev])
        {
            vis[ev]=;
            num[cur]++;
            num[cur]+=dfs(ev);

            for(int j=min(num[cur],m);j;--j)
              for(int k=min(num[ev],j-);k>=;--k)
                DP[cur][j]=max(DP[cur][j],DP[cur][j-k-]+DP[ev][k]+e[i].w);
        }
    }
    return num[cur];
}
int main()
{
    scanf("%d%d",&n,&m);
    for(re int i=;i<=n-;++i)
    {
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z);
        add(y,x,z);
    }
    vis[]=;
    dfs();
    printf("%d\n",DP[][m]);
    return ;
}