树状数组-HDU1541-Stars一维树状数组 POJ1195-Mobile phones-二维树状数组

树状数组，学长很早之前讲过，最近才重视起来，enmmmm。。。

树状数组(Binary Indexed Tree(B.I.T), Fenwick Tree)是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有元素之和，但是每次只能修改一个元素的值；经过简单修改可以在log(n)的复杂度下进行范围修改，但是这时只能查询其中一个元素的值(如果加入多个辅助数组则可以实现区间修改与区间查询)。

树状数组和线段树很像，但能用树状数组解决的问题，基本上都能用线段树解决，而线段树能解决的树状数组不一定能解决。相比较而言，树状数组效率要高很多。

 

观察这个图ヾ(◍°∇°◍)ﾉﾞ

C1 = A1

C2 = A1 + A2

C3 = A3

C4 = A1 + A2 + A3 + A4

C5 = A5

C6 = A5 + A6

C7 = A7

C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8

...

C16 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8 + A9 + A10 + A11 + A12 + A13 + A14 + A15 + A16

 

感觉很神奇，是怎么做到这样的呢。

哈，全靠二进制。

将数组的节点序号都转化成二进制。

 

就是这样的:

1--->001     C1 = A1

2--->010     C2 = A1 + A2

3--->011     C3 = A3

4--->100     C4 = A1 + A2 + A3 + A4

5--->101     C5 = A5

6--->110     C6 = A5 + A6     

7--->111     C7 = A7

8--->1000  C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8

 

但是这又有什么关系呢？!!!∑(ﾟДﾟノ)ノ

度娘说了：

这里有一个有趣的性质：

设节点编号为x，那么这个节点管辖的区间为2^k（其中k为x二进制末尾0的个数）个元素。因为这个区间最后一个元素必然为Ax，

所以很明显：Cn = A(n – 2^k + 1) + A(n-2^k+2)+... + An

 

什么意思呢？举个栗子，1对应的二进制是001，二进制末尾0的个数为0，所以k=0，

所以C1=A(1-2^k+1)+...An 就是C1=A(1-2^0+1)=A(1);

 

再来个栗子，4对应的二进制是100，二进制末尾0的个数为2，所以k=2，

所以C4=A(4-2^2+1)+A(4-2^2+2)+...+A(4)=A(1)+A(2)+A(3)+A(4);

 

再搞不懂就自己再手推几个数试试就可以了。

 

至于怎么得出来的这个神奇的东西，就是靠二进制啦。总结出来这个式子的人好厉害((✧◡✧))

 

接下来就是怎么代码实现这个呢？

就是要靠神奇的lowbit了。

 

int lowbit(int x)
{
 return x&(-x);
}

x&(-x)就是整数x与其相反数(负号取反)的按位与:相同位的两个数字都为1，则为1；若有一个不为1，则为0，即:1&1=1,0&1=0,0&0=0;

计算机中负数使用对应正数的补码来表示。

-x就是x对应的二进制数先各位取反，0变成1，1变成0。然后最低位加1。

举个栗子，4对应二进制为100；-4对应的为011+1=100，所以为(100)&(100)所以为100。

知道这个又能干嘛呀，就可以进行区间查询啦。

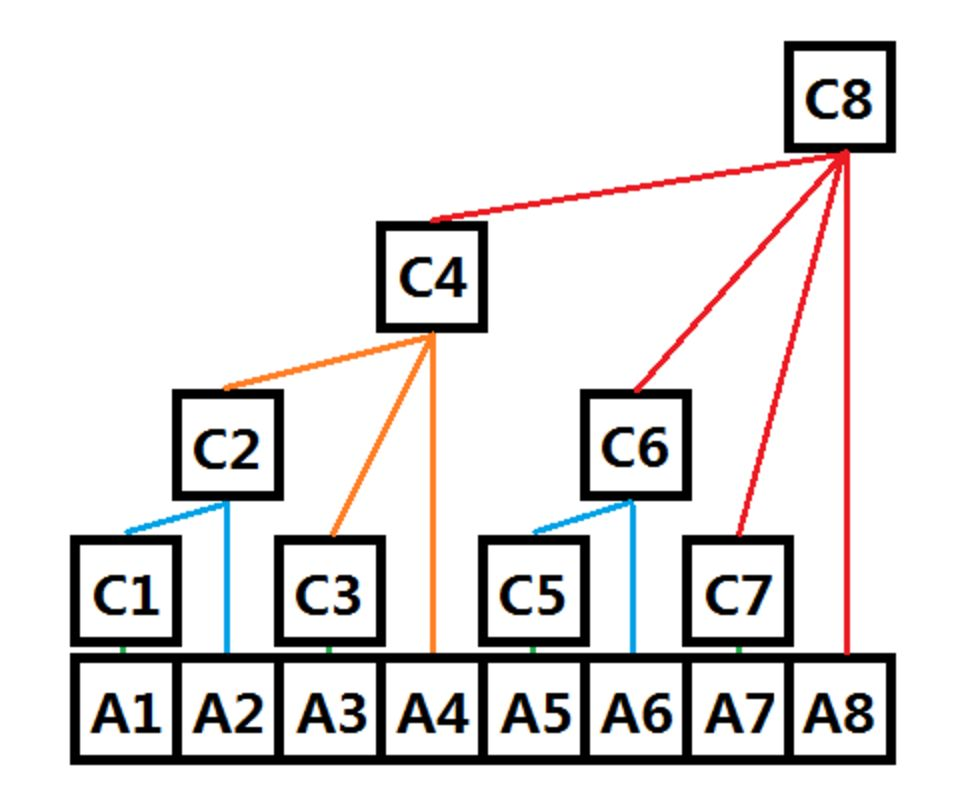
区间查询利用C[i]求A数组前i个的和；

//代码1：
int SUM(int n)
{
    int s=;
    while(n>){
        s+=c[n];
        n-=lowbit(n);
    }
    return s;
}

//代码2：
int SUM(int n)
{
    int s=;
    for(int i=n;i>;i-=lowbit(i))
         s+=c[i];
    return s;
}

两个代码哪个好理解理解哪个。

接着刚刚举的栗子4，求A数组前4个数的和；

lowbit(4)得出100；然后100就是4，所以为s+=c[4];此时i=4,4-lowbit(4)=100-100=0;结束。

再举个栗子7，求前7个数的和，就是s+=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7];

因为

1--->001     C1 = A1

2--->010     C2 = A1 + A2

3--->011     C3 = A3

4--->100     C4 = A1 + A2 + A3 + A4

5--->101     C5 = A5

6--->110     C6 = A5 + A6     

7--->111     C7 = A7

8--->1000  C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8

 

所以为C[4]+C[6]+C[7];

就是C[100]+C[110]+C[111];

 

首先s+=c[7];

然后lowbit[7]=(111)&(001)=001;此时i=7,所以为7-lowbit(7)=111-001=110,110就是6;s+=c[6];

       lowbit(6)=(110)&(010)=010;此时i=6,所以为6-lowbit(6)=110-010=100,100就是4;s+=c[4];

       lowbit(4)=(100)&(100)=100;此时i=4,所以为4-lowbit(4)=100-100=0,结束。

 

所以得到A数组中前7个数的和为C[7]+C[6]+C[4];

不懂的话再自己手推一个数就差不多懂了。

 

接下来就是单点更新。

单点更新要从下往上依次更新。

 

//代码1:
void add(int x)
{
    while(x<=N){
        ++a[x];
        x+=lowbit(x);
    }
}

//代码2:
void add(int x,int y)
{
    for(int i=x;i<=n;i+=lowbit(i))
        c[i]+=y;
}

更新过程仔细想一想就是查询过程的逆过程；

举个栗子，更新A1,还要继续更新C[1],C[2],C[4],C[8];

就是C[001],C[010],C[100],C[1000];

i=1;C[1]+=A[1];

lowbit(1)=(001)&(001)=001;此时i=1,所以为1+lowbit(1)=001+001=010,010就是2;C[2]+=A[1];

lowbit(2)=(010)&(110)=010;此时i=2,所以为2+lowbit(2)=010+010=100,100就是4;C[4]+=A[1];

lowbit(4)=(100)&(100)=100;此时i=4,所以为4+lowbit(4)=100+100=1000,1000就是8;C[8]+=A[1];结束。

好了，理解了树状数组就开始贴代码了。(；´д｀)ゞ

HDU1541-Stars

Stars

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 10611    Accepted Submission(s): 4240

Problem Description

Astronomers often examine star maps where stars are represented by points on a plane and each star has Cartesian coordinates. Let the level of a star be an amount of the stars that are not higher and not to the right of the given star. Astronomers want to know the distribution of the levels of the stars.

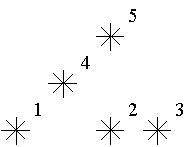
For example, look at the map shown on the figure above. Level of the star number 5 is equal to 3 (it's formed by three stars with a numbers 1, 2 and 4). And the levels of the stars numbered by 2 and 4 are 1. At this map there are only one star of the level 0, two stars of the level 1, one star of the level 2, and one star of the level 3.

You are to write a program that will count the amounts of the stars of each level on a given map.

 

Input

The first line of the input file contains a number of stars N (1<=N<=15000). The following N lines describe coordinates of stars (two integers X and Y per line separated by a space, 0<=X,Y<=32000). There can be only one star at one point of the plane. Stars are listed in ascending order of Y coordinate. Stars with equal Y coordinates are listed in ascending order of X coordinate.

 

Output

The output should contain N lines, one number per line. The first line contains amount of stars of the level 0, the second does amount of stars of the level 1 and so on, the last line contains amount of stars of the level N-1.

 

Sample Input

5

1 1

5 1

7 1

3 3

5 5

 

Sample Output

1

2

1

1

0

 

 

 

 

代码:

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<bitset>
 #include<cassert>
 #include<cctype>
 #include<cmath>
 #include<cstdlib>
 #include<ctime>
 #include<deque>
 #include<iomanip>
 #include<list>
 #include<map>
 #include<queue>
 #include<set>
 #include<stack>
 #include<vector>
 using namespace std;
 typedef long long ll;

 const double PI=acos(-1.0);
 const double eps=1e-;
 const ll mod=1e9+;
 const int inf=0x3f3f3f3f;
 const int maxn=1e5+;
 const int maxm=+;
 #define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);

 int a[maxn],ans[maxn];

 int lowbit(int x)
 {
     return x&(-x);
 }

 int getsum(int n)
 {
     int ans=;
     for(int i=n;i>;i-=lowbit(i))
         ans+=a[i];
     return ans;
 }

 void add(int x)
 {
     for(int i=x;i<=maxn;i+=lowbit(i))
         ++a[i];
 }

 int main(){
     int n,x,y;
     while(~scanf("%d",&n)){
         memset(a,,sizeof(a));
         memset(ans,,sizeof(ans));
         for(int i=;i<n;i++){
             scanf("%d%d",&x,&y);
             x++;
             ans[getsum(x)]++;
             add(x);
         }
         for(int i=;i<n;i++)
             printf("%d\n",ans[i]);
     }
     return ;
 }

溜了溜了。。。