降维之pca算法

pca算法:

算法原理：　pca利用的两个维度之间的关系和协方差成正比，协方差为０时，表示这两个维度无关,如果协方差越大这表明两个维度之间相关性越大，因而降维的时候，

都是找协方差最大的。

 将XX中的数据进行零均值化，即每一列都减去其均值。
 计算协方差矩阵C=1mXTXC=1mXTX
 求出CC的特征值和特征向量
 将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k行组成矩阵P
 Y=XPY=XP就是降维到k维后的数据。

代码：

# coding=utf-
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris

data = load_iris()

y = data.target
X = data.data
print data.feature_names
print data.data;
pca = PCA(n_components=)
reduced_X = pca.fit_transform(X)

red_x, red_y = [], []
blue_x, blue_y = [], []
green_x, green_y = [], []

for i in range(len(reduced_X)):
    if y[i] == :
        red_x.append(reduced_X[i][])
        red_y.append(reduced_X[i][])
    elif y[i] == :
        blue_x.append(reduced_X[i][])
        blue_y.append(reduced_X[i][])
    else:
        green_x.append(reduced_X[i][])
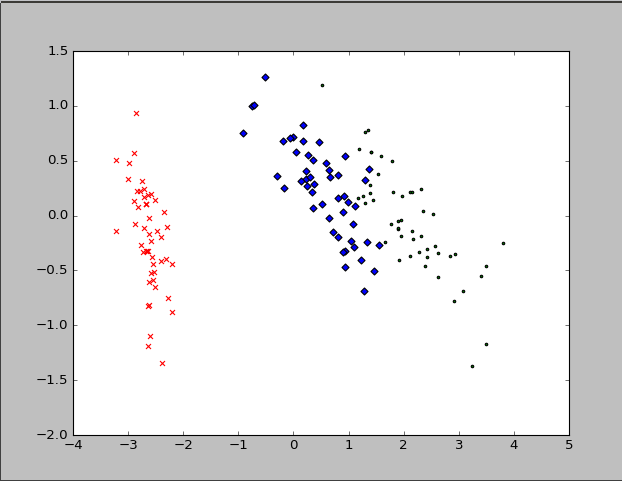
        green_y.append(reduced_X[i][])

plt.scatter(red_x, red_y, c='r', marker='x')
plt.scatter(blue_x, blue_y, c='b', marker='D')
plt.scatter(green_x, green_y, c='g', marker='.')
plt.show()