Rodrigues(罗德里格斯)旋转公式推导
1、
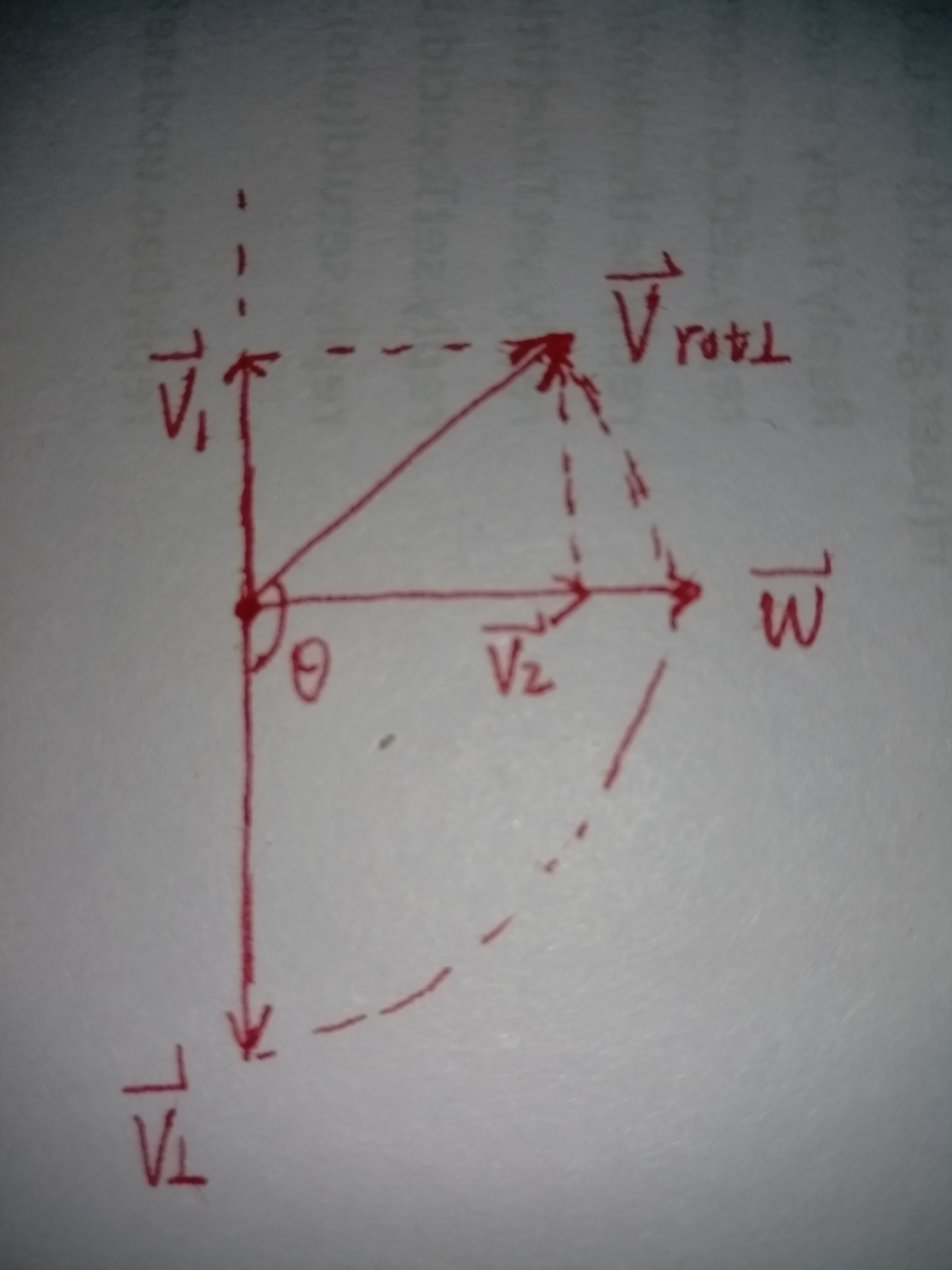
2、推导过程：我们的目的是求得vrot,所以应该求得v||和vrot在垂直于k方向的投影向量。
其中，
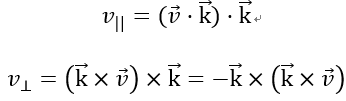
俯视图看：
此外，另一种表示方法为：
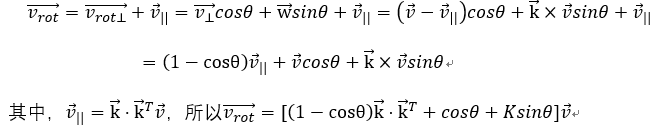
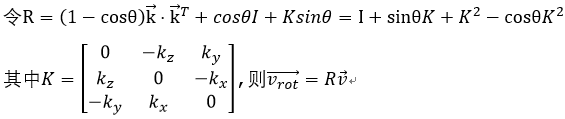
R可以看作旋转矩阵。
Rodrigues(罗德里格斯)旋转公式推导的更多相关文章
- Rodrigues Formula
https://en.wikipedia.org/wiki/Rodrigues%27_formula https://en.wikipedia.org/wiki/Rodrigues%27_rotati ...
- CS184.1X 计算机图形学导论 罗德里格斯公式推导
罗德里格斯公式推导 图1(复制自wiki) 按照教程里,以图1为例子,设k为旋转轴,v为原始向量. v以k为旋转轴旋转,旋转角度为θ,旋转后的向量为vrot. 首先我们对v进行分解,分解成一个平行于k ...
- 罗德里格斯旋转公式（Rodrigues' rotation formula）推导
本文综合了几个相关的维基百科,加了点自己的理解,从比较基础的向量投影和叉积讲起,推导出罗德里格斯旋转公式.公式比较繁杂,如有错误,欢迎评论区指出. 对于向量的三维旋转问题,给定旋转轴和旋转角度,用罗德 ...
- 从零开始一起学习SLAM | 三维空间刚体的旋转
刚体,顾名思义,是指本身不会在运动过程中产生形变的物体,如相机的运动就是刚体运动,运动过程中同一个向量的长度和夹角都不会发生变化.刚体变换也称为欧式变换. 视觉SLAM中使用的相机就是典型的刚体,相机 ...
- cnn公式推导
CNN公式推导 1 前言 在看此blog之前,请确保已经看懂我的前两篇blog[深度学习笔记1(卷积神经网络)]和[BP算法与公式推导].并且已经看过文献[1]的论文[Notes on Convolu ...
- 解释一下核主成分分析(Kernel Principal Component Analysis, KPCA)的公式推导过程（转载）
KPCA,中文名称”核主成分分析“,是对PCA算法的非线性扩展,言外之意,PCA是线性的,其对于非线性数据往往显得无能为力,例如,不同人之间的人脸图像,肯定存在非线性关系,自己做的基于ORL数据集的实 ...
- OpenCV 图像旋转实现
1 旋转矩形 首先建议阅读图像旋转算法原理-旋转矩阵,这篇博客可以让你很好地理解图像中的每一个点是如何进行旋转操作的.其中涉及到了图像原点与笛卡尔坐标原点之间的相互转换以及点旋转的一些公式推导. 这里 ...
- 核主成分分析(Kernel Principal Component Analysis, KPCA)的公式推导过程
KPCA,中文名称”核主成分分析“,是对PCA算法的非线性扩展,言外之意,PCA是线性的,其对于非线性数据往往显得无能为力,例如,不同人之间的人脸图像,肯定存在非线性关系,自己做的基于ORL数据集的实 ...
- PID算法 旋转倒立摆与平衡车的区别。此贴后边会更新。
我做PID算法的背景和经历:本人之前电子信息科学与技术专业,对控制方向颇感兴趣,刚上大学时听到实验室老师说PID算法,那年在暑假集训准备全国电子设计竞赛,我正在练习做一个以前专科的题目,帆板角度控制系 ...
随机推荐
- Qt绘制字体并获取文本宽度
参考资料: https://blog.csdn.net/liang19890820/article/details/51227894 QString text("abc");QPa ...
- 学习笔记-AngularJs（五）
之前的页面太丑了,后来我引入了bootstrap.css,把样式进行修了一番,如下图(一不小心,插入个链接,忽略,http://t.cn/RUbL4rP): (链接:http://www.live08 ...
- 【框架】selenium运行失败后自动截图（三）
思路: 1.写一个类继承TestListenerAdapter,覆写onTestFailure()方法 2.在onTestFailure方法里,调用selenium的TakesScreenShot的g ...
- scratch如何获取透明的图片
scratch中,每个对象都有一个造型,这个造型可以是载入外部的图片,但是外部图片很多是有背景的,放入scratch舞台区,有背景,很是不爽.用wps2016的ppt演示, 把文本框等另存为图片,图片 ...
- day05列表 类型
基本使用 1用途:记录多个值,比如人的多个爱好 # ======================================基本使用================================ ...
- unity中制作模拟第一人称视角下的指南针
private int zRotation; public GameObject obj; public void Update() { //obj = GameObject.Find("C ...
- flask使用配置文件
引入配置 app = Flask(__name__) app.config.from_pyfile('config.py') config.py DEBUG = True SECRET_KEY = '
- Java多线程习题 ===重点 ，错题积累
多线程重点,错题分析 1: 2: 3: 4: 5: 6: 7: 8: 9: 10: . 12: 13: 14: 15:
- mysql数据库存储引擎及区别
MySQL有多种存储引擎,每种存储引擎有各自的优缺点,可以择优选择使用:MyISAM.InnoDB.MERGE.MEMORY(HEAP).BDB(BerkeleyDB).EXAMPLE.FEDERAT ...
- node(2) EventEmitter类 事件队列 事件和error事件方法
事件队列的核心:事件触发与事件监听器功能的封装. // 引入 events 模块 var events = require('events'); // 创建 eventEmitter 对象 var e ...