[洛谷P2261] [CQOI2007]余数求和

洛谷题目链接:[CQOI2007]余数求和

题目背景

数学题，无背景

题目描述

给出正整数n和k，计算G(n, k)=k mod 1 + k mod 2 + k mod 3 + … + k mod n的值，其中k mod i表示k除以i的余数。例如G(10, 5)=5 mod 1 + 5 mod 2 + 5 mod 3 + 5 mod 4 + 5 mod 5 …… + 5 mod 10=0+1+2+1+0+5+5+5+5+5=29

输入输出格式

输入格式：

两个整数n k

输出格式：

答案

输入输出样例

输入样例#1：

10 5

输出样例#1：

29

说明

30%: n,k <= 1000

60%: n,k <= 10^6

100% n,k <= 10^9

一句话题意: 给出\(n,k(n,k<=10^9)\),求$$\sum_{i=1}^{n}k\mod i$$

题解: 学习这个之前我们首先需要知道什么是整除分块.

那么对于一个块内,所有的\(\lfloor \frac n i \rfloor\)都是一样的.但是如果我还想让一个块内所有的\(\lfloor \frac n i \rfloor\)都一样该怎么办呢?我们来看一张图(竖线是块与块的分界线):

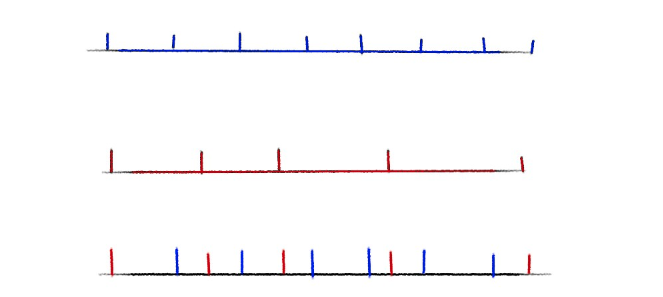
其实我们可以将原来的一个块再拆成几个块再计算.

既然知道了这个方法,我们就可以继续化简式子了.

\[ans=\sum_{i=1}^{n}k\mod i
\]

\[ans=\sum_{i=1}^{n}k-\lfloor \frac{k}{i}\rfloor \times i
\]

根据我们分的块,在同一个块内的\(\lfloor \frac{k}{i}\rfloor\)和\(\lfloor \frac{n}{i}\rfloor\)是一样的,所以这个块内的答案也就可以用\((r-l+1) \times (k \mod l+k \mod r)/2\)表示,然后再判断下一个区间的位置就可以了.

很好想的,代码也很好理解,如果不懂可以看代码再理解一下.

#include<bits/stdc++.h>
using namespace std;
typedef int _int;
#define int long long

int n, k, ans = 0;

_int main(){
    cin >> n >> k;
    int l = 1, rn, rk, lim = min(n, k);
    while(l <= lim){
        rn = n/(n/l), rk = k/(k/l);
        if(rn < rk) ans += (rn-l+1)*(k%l+k%rn)/2, l = rn+1;
        else ans += (rk-l+1)*(k%l+k%rk)/2, l = rk+1;
    }
    if(lim == k) ans += (n-k)*k;
    cout << ans << endl;
    return 0;
}