概率+后效性处理——cf930B好题

之前题目看错了。。

先用双倍字符串处理后效性
首先要确定一个结论：如果原串s中相距为d的ch1和ch2只有一对，那么如果第一个翻开ch1，第二个翻开ch2，就能确定k
现在要求的是当我们第一次翻开的是ch1时，第二次翻哪个位置成功的概率最高
设这个概率为p，ans=sigma(cnti/n * pi),i∈['a','z']
那么我们枚举d，对每种字符找到这个最大的d即可 

.

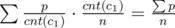#include<bits/stdc++.h>
using namespace std;
int n,mp[][][];
char s[<<];

int main(){
    cin>>s;
    n=strlen(s);
    for(int i=;i<n;i++)
        s[i+n]=s[i];
    for(int i=;i<n;i++)
        for(int j=i+;j<i+n;j++)
            mp[s[i]-'a'][s[j]-'a'][j-i+]++;
    int    sum=;
    for(int i=;i<;i++){//对于每个字符找d
        int Max=;
        for(int d=;d<=n;d++){
            int tmp=;
            for(int j=;j<;j++)
                if(mp[i][j][d]==)tmp++;
            Max=max(Max,tmp);
        }
        sum+=Max;
    }
    printf("%.10lf\n",1.0*sum/n);
}