线性回归和梯度下降代码demo

程序所用文件：https://files.cnblogs.com/files/henuliulei/%E5%9B%9E%E5%BD%92%E5%88%86%E7%B1%BB%E6%95%B0%E6%8D%AE.zip

线性回归

决定系数越接近一那么预测效果越好

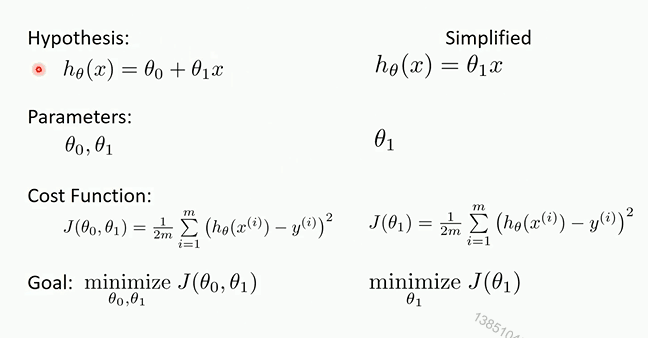
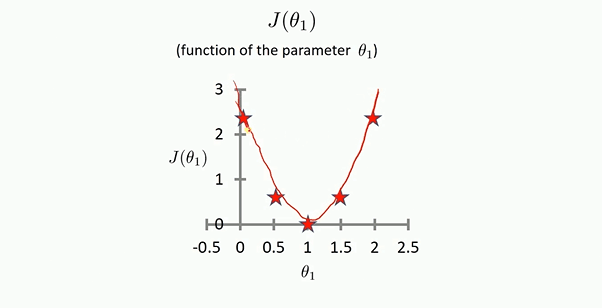
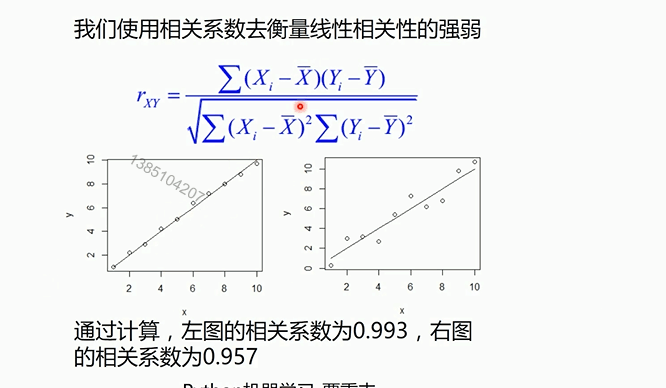
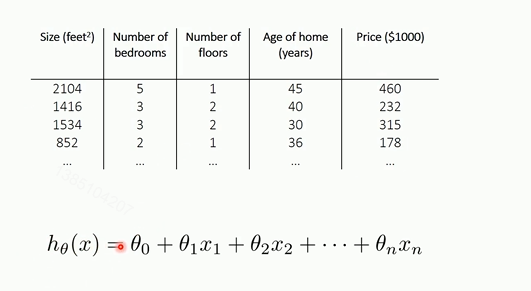
对于多元线性回归和一元线性回归推导理论是一致的，只不过参数是多个参数而已

梯度下降

梯度下降法存在局部最小值

太小迭代次数多，太大将无法迭代到最优质

梯度下降发容易到达局部最小值

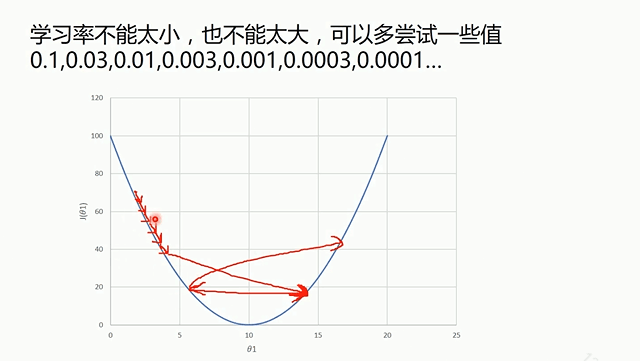
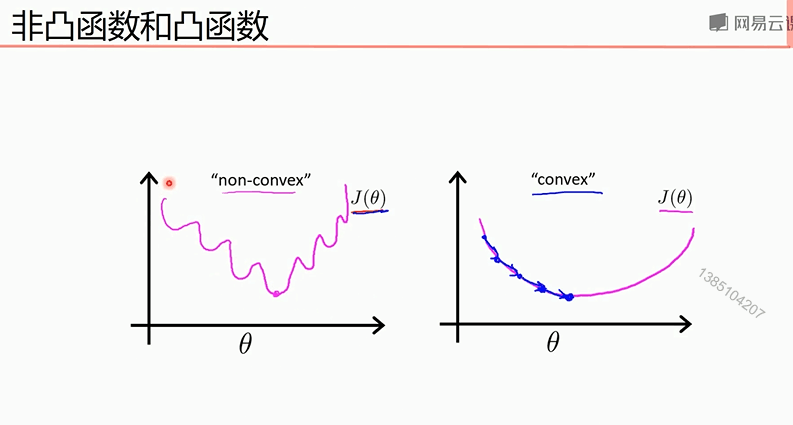
凸函数使用局部下降法一定可以到全部最小值，所以不存在局部最小值才可以

下面两个demo是一元函数的拟合

1使用梯度下降法的数学公式进行的机器学习代码

 import numpy as np
 from matplotlib import  pyplot as plt
 #读取数据
 data = np.genfromtxt('data.csv',delimiter=',')
 x_data = data[:, ]
 y_data = data[:, ]
 #plt.scatter(x_data, y_data)
 #plt.show()
 lr = 0.0001
 k =
 b =
 epochs =
 def compute_loss(x_data, y_data, b, k):#计算损失函数
     m = float(len(x_data))
     sum =
     for i in range(, len(x_data)):
         sum += (y_data[i] - (k*x_data[i] + b))**
     return sum/(*m)
 def gradient(x_data, y_data, k, b, lr, epochs):#进行梯度下降
     m = float(len(x_data))
 
     for i in range(,epochs):
         k_gradient =
         b_gradiet =
         for j in range(,len(x_data)):
             k_gradient += (/m)*((x_data[j] * k + b) - y_data[j])
             b_gradiet += (/m)*((x_data[j] * k + b) - y_data[j]) * x_data[j]
         k -= lr * k_gradient
         b -= lr * b_gradiet
 
         if i %  == :
             print(i)
             plt.plot(x_data, y_data, 'b.')
             plt.plot(x_data, k*x_data + b, 'r')
             plt.show()
 
     return k, b
 
 k,b = gradient(x_data, y_data, , , lr, epochs)
 plt.plot(x_data, k * x_data + b, 'r')
 plt.plot(x_data, y_data, 'b.')
 print('loss =:',compute_loss(x_data, y_data, b, k),'b =:',b,'k =:',k)
 plt.show()

2 使用Python的sklearn库

 import numpy as np
 from matplotlib import  pyplot as plt
 from sklearn.linear_model import LinearRegression
 #读取数据
 data = np.genfromtxt('data.csv',delimiter=',')
 x_data = data[:, ]
 y_data = data[:, ]
 plt.scatter(x_data, y_data)
 plt.show()
 x_data = data[:, , np.newaxis]#使一位数据编程二维数据
 y_data = data[:, , np.newaxis]
 model =LinearRegression()
 model.fit(x_data, y_data)#传进的参数必须是二维的
 plt.plot(x_data, y_data, 'b.')
 plt.plot(x_data, model.predict(x_data), 'r')#画出预测的线条
 plt.show()

3使用梯度下降法完成多元线性回归（以二元为例）

 import numpy as np
 from numpy import genfromtxt
 import matplotlib.pyplot as plt
 from mpl_toolkits.mplot3d import Axes3D #用来画3D图的包
 # 读入数据
 data = genfromtxt(r"Delivery.csv",delimiter=',')
 print(data)
 # 切分数据
 x_data = data[:,:-]
 y_data = data[:,-]
 print(x_data)
 print(y_data)
 # 学习率learning rate
 lr = 0.0001
 # 参数
 theta0 =
 theta1 =
 theta2 =
 # 最大迭代次数
 epochs = 
 
 # 最小二乘法
 def compute_error(theta0, theta1, theta2, x_data, y_data):
     totalError =
     for i in range(, len(x_data)):
         totalError += (y_data[i] - (theta1 * x_data[i,] + theta2*x_data[i,] + theta0)) **
     return totalError / float(len(x_data))
 
 def gradient_descent_runner(x_data, y_data, theta0, theta1, theta2, lr, epochs):
     # 计算总数据量
     m = float(len(x_data))
     # 循环epochs次
     for i in range(epochs):
         theta0_grad =
         theta1_grad =
         theta2_grad =
         # 计算梯度的总和再求平均
         for j in range(, len(x_data)):
             theta0_grad += (/m) * ((theta1 * x_data[j,] + theta2*x_data[j,] + theta0) - y_data[j])
             theta1_grad += (/m) * x_data[j,] * ((theta1 * x_data[j,] + theta2*x_data[j,] + theta0) - y_data[j])
             theta2_grad += (/m) * x_data[j,] * ((theta1 * x_data[j,] + theta2*x_data[j,] + theta0) - y_data[j])
         # 更新b和k
         theta0 = theta0 - (lr*theta0_grad)
         theta1 = theta1 - (lr*theta1_grad)
         theta2 = theta2 - (lr*theta2_grad)
     return theta0, theta1, theta2
 print("Starting theta0 = {0}, theta1 = {1}, theta2 = {2}, error = {3}".
       format(theta0, theta1, theta2, compute_error(theta0, theta1, theta2, x_data, y_data)))
 print("Running...")
 theta0, theta1, theta2 = gradient_descent_runner(x_data, y_data, theta0, theta1, theta2, lr, epochs)
 print("After {0} iterations theta0 = {1}, theta1 = {2}, theta2 = {3}, error = {4}".
       format(epochs, theta0, theta1, theta2, compute_error(theta0, theta1, theta2, x_data, y_data)))
 ax = Axes3D(plt.figure())#和下面的代码功能一样
 #ax = plt.figure().add_subplot(, projection='3d')#plt.figure().add_subplot和plt.subplot的作用是一致的
 ax.scatter(x_data[:, ], x_data[:, ], y_data, c='r', marker='o', s=)  # 点为红色三角形
 x0 = x_data[:, ]
 x1 = x_data[:, ]
 # 生成网格矩阵
 x0, x1 = np.meshgrid(x0, x1)#生成一个网格矩阵，矩阵的每个点的第一个轴的取值来自于x0范围内，第二个坐标轴的取值来自于x1范围内
 z = theta0 + x0 * theta1 + x1 * theta2
 # 画3D图
 ax.plot_surface(x0, x1, z)
 # 设置坐标轴
 ax.set_xlabel('Miles')
 ax.set_ylabel('Num of Deliveries')
 ax.set_zlabel('Time')
 
 # 显示图像
 plt.show()

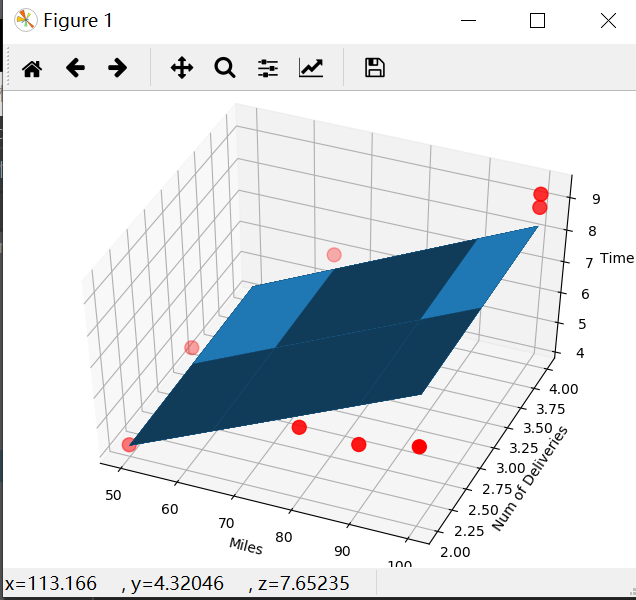
4：使用Python的sklearn库完成多元线性回归

import numpy as np
from numpy import genfromtxt
from sklearn import linear_model
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 读入数据
data = genfromtxt(r"Delivery.csv",delimiter=',')
print(data)
# 切分数据
x_data = data[:,:-]
y_data = data[:,-]
print(x_data)
print(y_data)
# 创建模型
model = linear_model.LinearRegression()
model.fit(x_data, y_data)
# 系数
print("coefficients:",model.coef_)
 
# 截距
print("intercept:",model.intercept_)
 
# 测试
x_test = [[,]]
predict = model.predict(x_test)
print("predict:",predict)
ax = plt.figure().add_subplot(, projection='3d')
ax.scatter(x_data[:, ], x_data[:, ], y_data, c='r', marker='o', s=)  # 点为红色三角形
x0 = x_data[:, ]
x1 = x_data[:, ]
# 生成网格矩阵
x0, x1 = np.meshgrid(x0, x1)
z = model.intercept_ + x0*model.coef_[] + x1*model.coef_[]
# 画3D图
ax.plot_surface(x0, x1, z)#参数是二维的，而model.prodict(x_data)是一维的。
# 设置坐标轴
ax.set_xlabel('Miles')
ax.set_ylabel('Num of Deliveries')
ax.set_zlabel('Time')
 
# 显示图像
plt.show()

5 多项式回归拟合

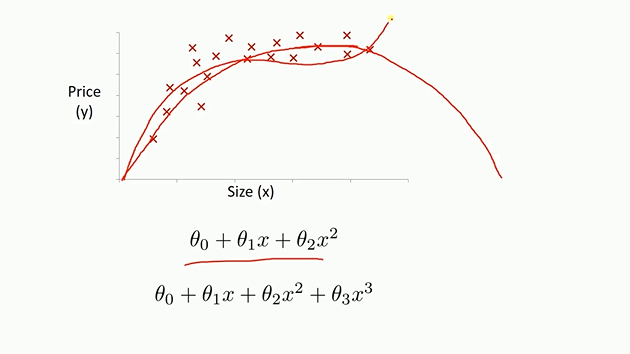
 import numpy as np
 import matplotlib.pyplot as plt
 from sklearn.preprocessing import PolynomialFeatures#多项式
 from sklearn.linear_model import LinearRegression
 
 # 载入数据
 data = np.genfromtxt("job.csv", delimiter=",")
 x_data = data[:,]
 y_data = data[:,]
 plt.scatter(x_data,y_data)
 plt.show()
 x_data
 x_data = x_data[:,np.newaxis]
 y_data = y_data[:,np.newaxis]
 x_data
 # 创建并拟合模型
 model = LinearRegression()
 model.fit(x_data, y_data)
 # 画图
 plt.plot(x_data, y_data, 'b.')
 plt.plot(x_data, model.predict(x_data), 'r')
 plt.show()
 # 定义多项式回归,degree的值可以调节多项式的特征
 poly_reg  = PolynomialFeatures(degree=)
 # 特征处理
 x_poly = poly_reg.fit_transform(x_data)
 # 定义回归模型
 lin_reg = LinearRegression()
 # 训练模型
 lin_reg.fit(x_poly, y_data)
 # 画图
 plt.plot(x_data, y_data, 'b.')
 plt.plot(x_data, lin_reg.predict(poly_reg.fit_transform(x_data)), c='r')
 plt.title('Truth or Bluff (Polynomial Regression)')
 plt.xlabel('Position level')
 plt.ylabel('Salary')
 plt.show()
 # 画图
 plt.plot(x_data, y_data, 'b.')
 x_test = np.linspace(,,)
 x_test = x_test[:,np.newaxis]
 plt.plot(x_test, lin_reg.predict(poly_reg.fit_transform(x_test)), c='r')
 plt.title('Truth or Bluff (Polynomial Regression)')
 plt.xlabel('Position level')
 plt.ylabel('Salary')
 plt.show()