【BZOJ 4663】 （最小割）

4663: Hack

Time Limit: 10 Sec  Memory Limit: 128 MB
Submit: 69  Solved: 26

Description

由于 FZYZ 教学区禁止使用手机，所以如何在一个课间通知到人就成了一个很大的问题。所幸，在不知道被信息传

递不及时坑了多少次之后，小叶子(@97littleleaf11)完美地解决了这个问题。小叶子组建了一张关系网，每一个

人是这张关系网上的一个节点(节点编号为[0,n-1])，两个人之间的通讯关系就是这张网上的一条有向边(一条 u->

v 的边意味着信息可以从u 传递到 v)。小叶子是 0 号节点，也是信息的发出者，n+e 是 n-1 号节点，在这个问

题中，他就是信息的接受者。一条信息从小叶子出发，可以沿着任意的边传递，最终传递给 n+e。在这个过程中，

一个人(包括小叶子和 n+e)可以经过多次，一条边也可以经过多次。经过多年的观察，小叶子发现这张关系网的每

一条边都是有可能被hack 的！当然每条边 hack 的代价是不一样的。所以，小叶子想要评价这个关系网的安全程

度。试想你要入侵这一张关系网，那么你只能事先选择一些边，将这些边hack 掉。如果一条边被 hack 了，就意

味着当信息从这条边传递的时候就会被截获。当然 n+e 也是非常厉害的！如果一条信息在传递过程中被截获两次

及以上，那么 n+e 就能用强大的智商定位出你的位置，那么这一次入侵就必然会失败。当然，如果 n+e 接收到了

消息，但是这条消息没有被截获，那么这次入侵也就是失败的。更精确地说，一次成功的入侵要满足以下条件：对

于任意一种可能的传递信息的方式(对应着一条从 0 到 n-1 的路径)，必须经过恰好一次被hack 的边。一次入侵

的代价就是你选择 hack 掉的边的代价和。小叶子想要知道，如果你拥有 n+e 这样超神的智商，而你又想最小化

代价，那么你入侵的代价会是多少呢？

Input

第一行 n，m。表示点数及边数

接下来 m 行，每行三个整数 u,v,w，表示一条从 u 到 v 的代价为 w 的边。

2<=n<=100,m<=2500,1<=w<=10^9，0<=u,v<n,保证存在至少一条从0到n-1的路径。

Output

输出一行，表示答案。,如果不存在合法的入侵方案，那么输出-1.

Sample Input

6 7
0 1 5
0 2 5
1 3 1
2 4 1
4 1 1
3 5 5
4 5 5

Sample Output

6
//hack 掉 0->1,2->4 这两条边

HINT

Source

【分析】

　　其实反向边建INF的想法有考虑过。但是不会证。很迷人。。。

　　送个迷人的图：

　　

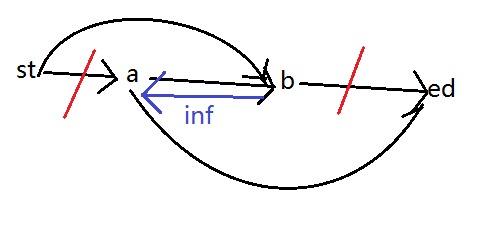
　　就是建了inf反向边，就不会同一路径的割了，因为并不会更好。。

　　然后要注意删掉st到不了的点，不然会有这样迷人的情况：

　　

　　st本来不会经过a到ed，但现在这样建INF，就一定要割掉一些边断掉它了。

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #include<queue>
 #include<stack>
 using namespace std;
 #define Maxn 110
 #define Maxm 2600
 #define LL long long
 const LL INF=(LL)*(LL)1e9;

 LL mymin(LL x,LL y) {return x<y?x:y;}

 struct node{int x,y,o,next;LL f;bool p;}t[Maxm*];
 bool vis[Maxn];
 int first[Maxn],len;

 void ins(int x,int y,LL f)
 {
     t[++len].x=x;t[len].y=y;t[len].f=f;
     t[len].next=first[x];first[x]=len;t[len].o=len+;
     t[++len].x=y;t[len].y=x;t[len].f=INF;
     t[len].next=first[y];first[y]=len;t[len].o=len-;
     t[len-].p=t[len].p=;
 }

 void dfs(int x)
 {
     vis[x]=;
     for(int i=first[x];i;i=t[i].next)
     {
         if(i%==) continue;
         int y=t[i].y;
         if(!vis[y]) dfs(y);
     }
 }

 int st,ed;
 int dis[Maxn];
 queue<int > q;
 bool bfs()
 {
     for(int i=;i<=ed;i++) dis[i]=-;
     while(!q.empty()) q.pop();
     dis[st]=;q.push(st);
     while(!q.empty())
     {
         int x=q.front();
         for(int i=first[x];i;i=t[i].next) if(t[i].p&&t[i].f>)
         {
             int y=t[i].y;
             if(!vis[y]) continue;
             if(dis[y]==-)
             {
                 dis[y]=dis[x]+;
                 q.push(y);
             }
         }
         q.pop();
     }
     if(dis[ed]==-) return ;
     return ;
 }

 LL ffind(int x,LL flow)
 {
     if(x==ed) return flow;
     LL now=;
     for(int i=first[x];i;i=t[i].next) if(t[i].p&&t[i].f>)
     {
         int y=t[i].y;
         if(dis[y]==dis[x]+)
         {
             LL a=ffind(y,mymin(flow-now,t[i].f));
             t[i].f-=a;
             t[t[i].o].f+=a;
             now+=a;
         }
         if(now==flow) break;
     }
     if(now==) dis[x]=-;
     return now;
 }

 void output()
 {
     for(int i=;i<=len;i++) if(t[i].p)
     {
         printf("%d -> %d %d\n",t[i].x,t[i].y,t[i].f);
     }printf("\n");
 }

 LL ans=;
 void max_flow()
 {
     while(bfs())
     {
         ans+=ffind(st,INF);
         if(ans>=INF) break;
     }
 }

 int main()
 {
     int n,m;
     scanf("%d%d",&n,&m);
     len=;
     memset(first,,sizeof(first));
     for(int i=;i<=m;i++)
     {
         int x,y;LL f;
         scanf("%d%d%lld",&x,&y,&f);
         x++;y++;
         ins(x,y,f);
     }
     for(int i=;i<=n;i++) vis[i]=;vis[]=;
     dfs();
     for(int i=;i<=len;i+=) if(vis[t[i].x]==) t[i].p=t[t[i].o].p=;
     st=;ed=n;
     // output();
     max_flow();
     if(ans>=INF) printf("-1\n");
     else printf("%lld\n",ans);
     return ;
 }

2017-03-31 08:26:56