【HDU】6410：序列期望

序列期望

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 247    Accepted Submission(s): 119

Problem Description 
“看似随机，实则早已注定”——光羽

度度熊有n个随机变量x1,x2,...,xnx1,x2,...,xn。给定区间[l1,r1],...,[ln,rn][l1,r1],...,[ln,rn]，变量xixi的值会等概率成为区间[li,ri][li,ri]中的任意一个整数。

显然这n个随机变量的值会有一共∏ni=1(ri−li+1)∏i=1n(ri−li+1) 种情况，且每种情况出现的概率为∏ni=11ri−li+1∏i=1n1ri−li+1

对于某种情况，令h=maxx1,x2,...,xnh=maxx1,x2,...,xn，定义这种情况的权值为：∏ni=1(h−xi+1)∏i=1n(h−xi+1).

度度熊想知道权值的期望是多少？请将答案对109+7取模后输出。

PS：不清楚期望是啥？为什么不问问神奇的百度呢？

Input 
第一行一个数，表示数据组数T。

每组数据第一行一个整数n；接下来n行，每行两个数，表示li和ri。

数据组数T=100，满足：

−1≤n≤100−1≤n≤100 
−1≤li≤ri≤104−1≤li≤ri≤104

其中70%的数据满足ri≤100。

Output 
每组数据输出一行，每行仅包含一个数，表示期望。

假设答案为pq，请输出p×q−1 mod 109+7，此处q−1为q的逆元。

Sample Input 
2 
3 
2 5 
2 4 
2 5 
3 
1 1 
2 3 
1 1

Sample Output 
875000012 
500000010

Hint

第二组数据的解释：序列只有两种情况（1,2,1）和(1,3,1)，权值分别为2*1*2=4和3*1*3=9，答案为(4+9)/2，在模域下为500000010。

 

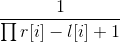 概率期望本来就学的好菜aaa！这道题还是挺有意思的。可以暴力枚举每一个最大值M，计算对应做出的贡献。而至少出现了一次M并且M是出现的最大值的概率就是每一段区间出现l[i]-M的贡献减去l[i]-(M-1)的贡献，因为每种情况出现的概率是，我们先把每个M的贡献加起来最后除以每种情况的概率就是答案。

#include<iostream>
#include<cstdio>
#include<algorithm>
#define RG register
#define ll long long
#define mod 1000000007
using namespace std;

int n;
ll l[], r[];

inline ll mpow ( ll a, ll b ) {
    ll ans = ;
    for ( ; b; b >>= , a = a * a % mod )
        if ( b &  ) ans = ans * a % mod;
    return ans;
}

int main ( ) {
    int T;
    scanf ( "%d", &T );
    while ( T -- ) {
        scanf ( "%d", &n );
        ll sum = , MI = , MA = ;
        for ( int i = ; i <= n; i ++ ) {
            scanf ( "%I64d%I64d", &l[i], &r[i] );
            sum = sum * ( r[i] - l[i] +  ) % mod;
            MI = max( l[i], MI );
            MA = max( MA, r[i] );
        }
        ll ans = ;
        for ( RG ll h = MI; h <= MA; h ++ ) {
            ll sum1 = , sum2 = ;
            for ( RG int i = ; i <= n; i ++ ) {
                ll L = l[i], R = min ( h, r[i] );
                L = h - L + , R = h - R + ;
                sum1 = ( L + R ) * ( L - R +  ) /  * sum1 % mod;
            }
            for ( RG int i = ; i <= n; i ++ ) {
                ll L = l[i], R = min ( h - , r[i] );
                L = h - L + , R = h - R + ;
                sum2 = ( L + R ) * ( L - R +  ) /  * sum2 % mod;
            }
            ans = ( ans + ( sum1 - sum2 + mod ) % mod ) % mod;
        }
        ans = ans * mpow( sum, mod -  ) % mod;
        printf ( "%I64d\n", ans );
    }
    return ;
}