字符串KMP算法详解

引入

字符串kmp算法用于解决字符串匹配的问题：

给出两个字符串 \(s_1\) 和 \(s_2\)，若 \(s_1\) 的区间 \([l, r]\) 子串与 \(s_2\) 完全相同，则称 \(s_2\) 在 \(s_1\) 中出现了，其出现位置为 \(l\)。 现在请你求出 \(s_2\) 在 \(s_1\) 中所有出现的位置。

• 很显然，我们能够想到暴力求解：

cin>>s1>>s2;
ll lena=s1.size(),lenb=s2.size();
for(int i=0;i<=lena-lenb;++i){
  bool flag=0;
  for(int j=i,k=1;j<i+lenb;++j,++k){
      if(s1[j]!=s2[k]){
           flag=1;
           break;
      }
  }
  if(!flag)cout<<i+1<<'\n';
}

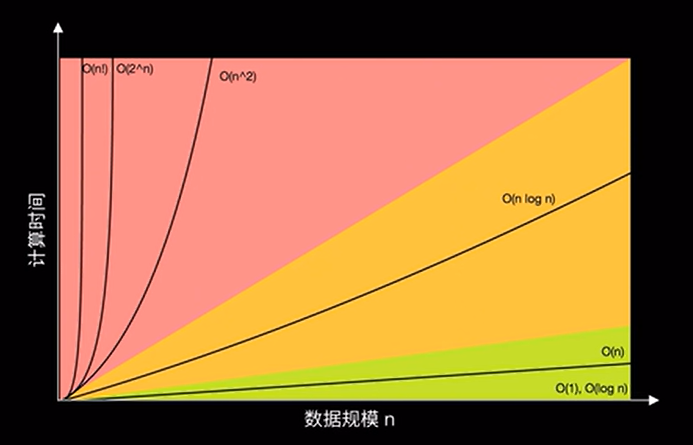
时间复杂度为 \(O(nm)\) ，显然是不被接受的。

• 接下来我们可以想到 字符串哈希

  字符串哈希详解

#include<iostream>
#include<cstdio>
#include<cstring>
#define ull unsigned long long
using namespace std;
const int N=1e6+10;
ull h[N],hs=0;
char s[N],t[N];
ull qp(ull x,ull y)
{
  ull now=x,ans=1;
  while(y)
  {
      if(y&1)
          ans*=now;
      now*=now;
      y>>=1;
  }
  return ans;
}
int main()
{
  cin>>s+1>>t+1;
  int l1=strlen(s+1),l2=strlen(t+1);
  for(int i=1;i<=l1;++i)
      h[i] = h[i-1]*131ull+s[i];
  for(int i=1;i<=l2;++i)
      hs = hs*131ull+t[i];
  int ans=0;
  for(int i=l2;i<=l1;++i)
  {
      ull now=h[i]-h[i-l2]*qp(131,l2);
      if(now==hs)
          ans++;
  }
  cout<<ans<<endl;
  return 0;
}

我们假设所给定的字符串允许 \(k\) 次失配 ， 时间复杂度为：\(O(m+kn· log_2^{m})\)

即使算法加入二分优化也卡不过硬性的匹配数据。

—— 那么，我们就可以考虑 字符串kmp算法

字符串kmp

设 \(s1 = a b a c a b a b , s2 = ababc\)

一开始，我们从 \(i=0\) 开始匹配：

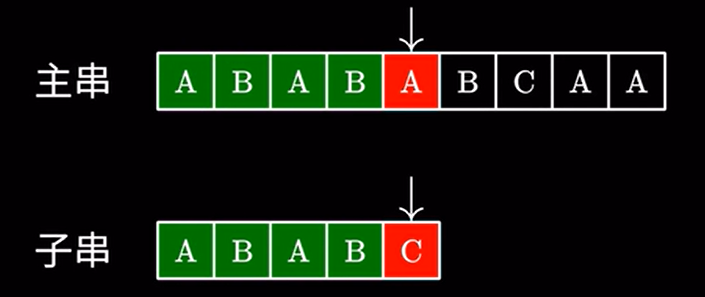
基本思想

kmp算法的具体思路是当我们发现某一个字符串不匹配的时候，由于已经知道之前遍历过的字符，利用这些信息来做一个 backup 的操作。

用上面的例子，我们在主串中搜索 \(ababc\) 发现最后一个字符不匹配。由于我们知道上面读过那些字符，我们将字串移动到这个位置：

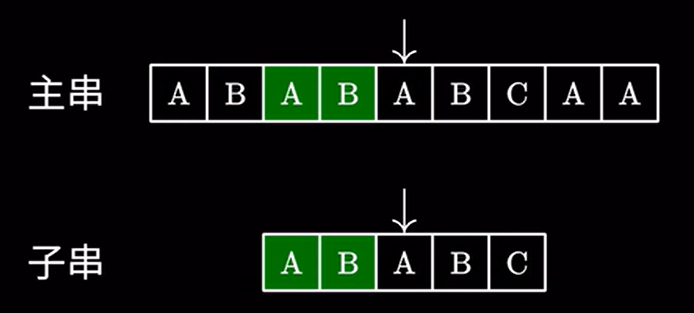
接着进行匹配，由于这里的 \(AB\) 和主串的 \(AB\) 相同，我们完全可以跳过他们，直接进行下一步的匹配：

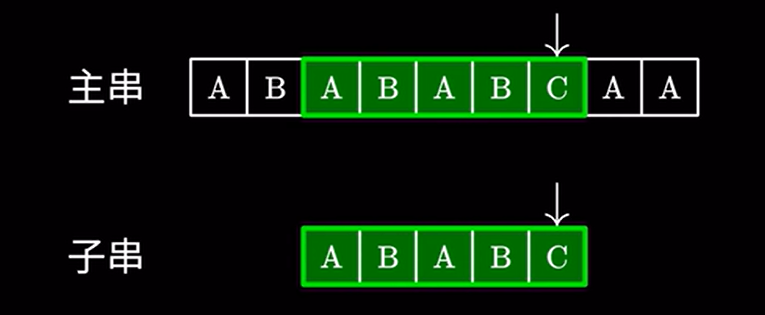
那我们怎么知道要跳过多少个字符呢？

——那就要用到 kmp 算法中的 next 数组了。

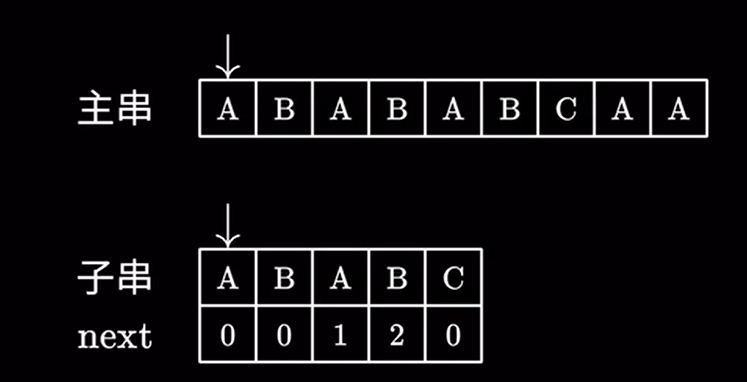
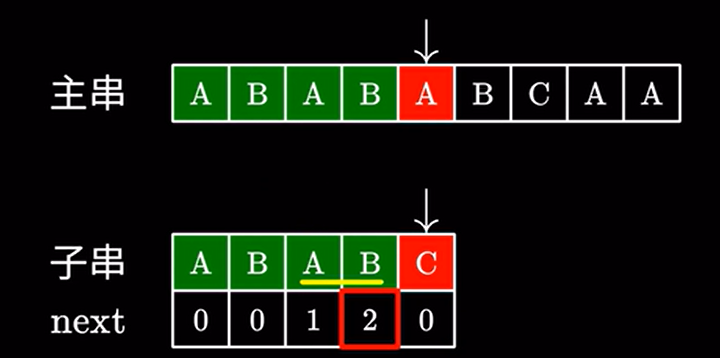
kmp算法在匹配失败的时候：

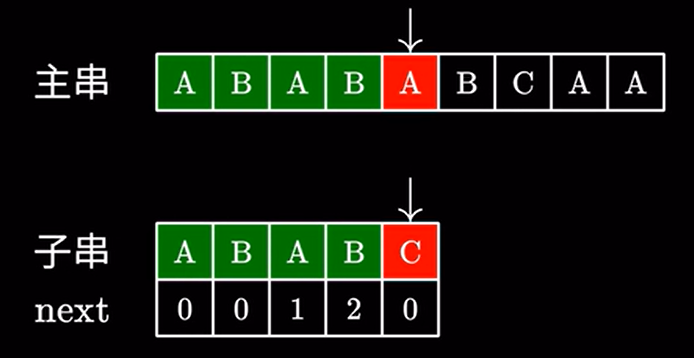
我们回去看最后一个匹配字符的next值：

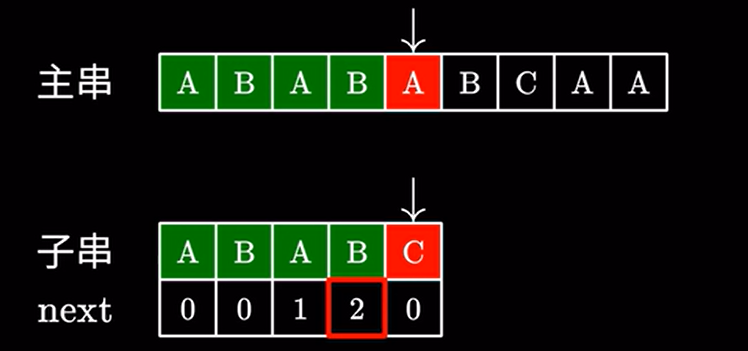
例如此处是 \(2\) 然后直接跳过 \(2\) 个字符：

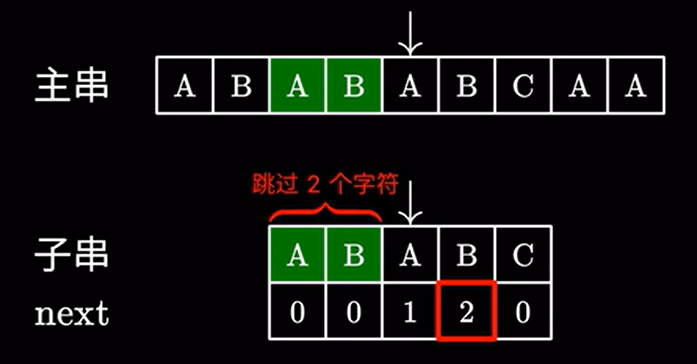
这里 \(2\) 代表子串中我们可以跳过的字符，也就是说前面的这个 \(AB\) 不需要看了，直接进行下一步匹配：

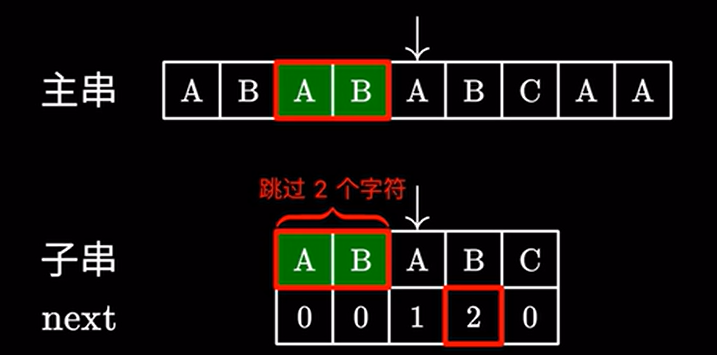
很显然，这样操作是没有问题的，因为主串中跳过的这两个 \(AB\) 确实可以和子串中的 \(AB\) 匹配上。所以我们只需要继续匹配后面的字符即可。

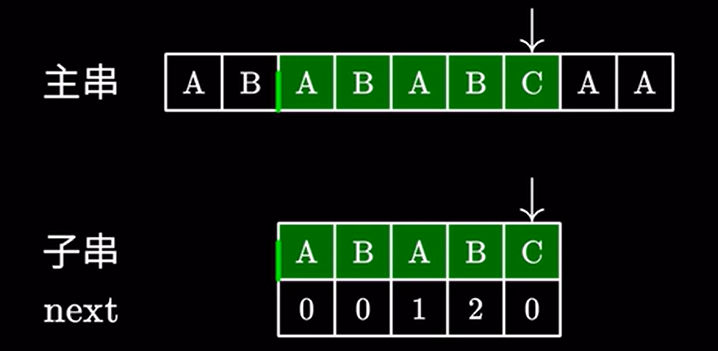
由于不用把时间浪费在无意义的失配上，效率自然也提高了不少。

next 数组的生成

原理&思路

之前我们讲了，next数组是在字符串匹配失败的时候可以跳过的字符数量。但凭什么可以这么做呢？

因为之前我们成功匹配了这两个 \(AB\)

和前面跳过的这两个 \(AB\) 是完全一致的：

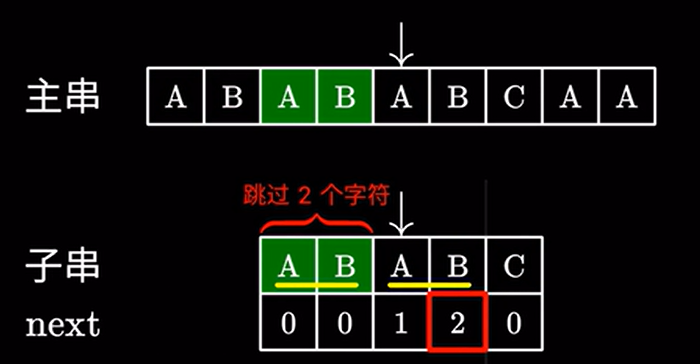
也就是说，多于字串的前 \(4\) 个字符，他们拥有相同的前缀的后缀 \(AB\) 长度为 \(2\)

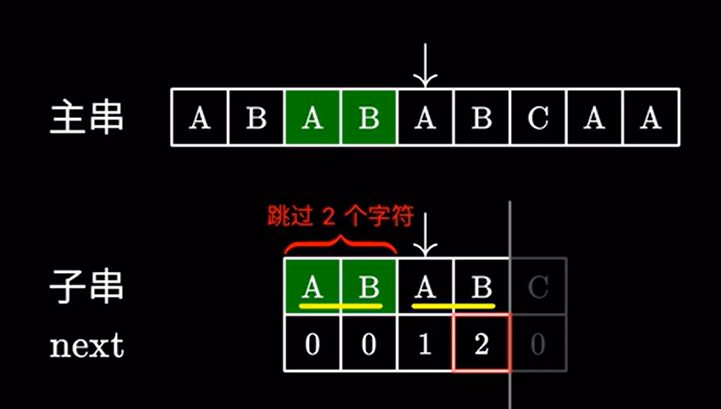
其实 next 数组本质就是寻找子串中相同且最长(真)前后缀的长度。

例如这里的 长度为 \(3\) 的相同前后缀 \(ABA\)

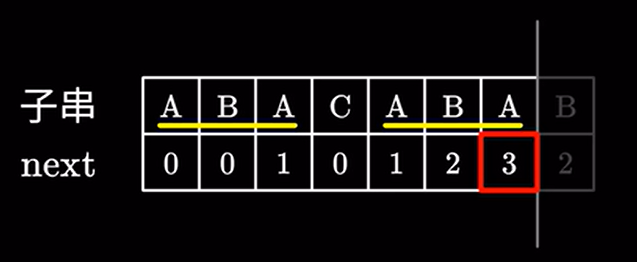
我们要找的前后缀必须是真前缀和真后缀，既不能是字符串本身。

我们还是用刚才的例子来解释，很显然对于第一个字符肯定不存在比他还短的前后缀，next 值直接为 \(0\)

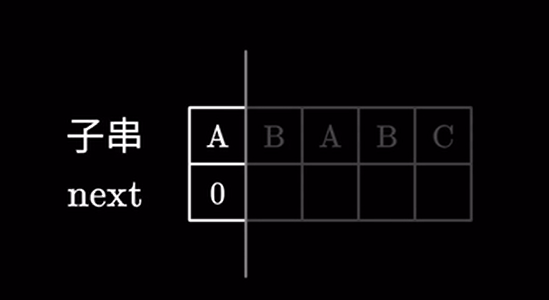
对于前两个字符同样不存在相同的前后缀，next 值为 \(0\)

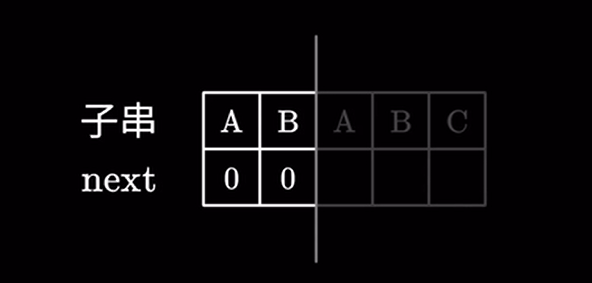
对于前 \(3\) 个字符，由于 \(A\) 是最长且相同的前后缀，所以为 \(1\)

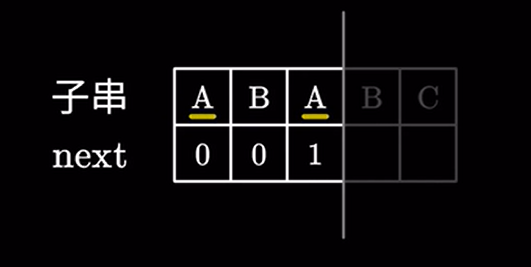
以此类推：

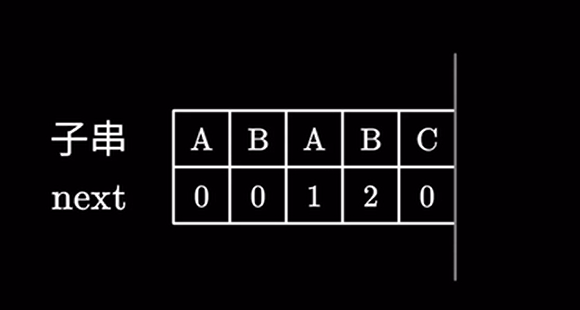
我们就得到了整个 next 数组，那算法应该怎么写呢？

具体操作

算法实现我们可以采用一种递推的思路来求解，他可以不断地利用已经掌握的信息来避免重复的计算。

假设我们已经知道当前共同的前后缀了：

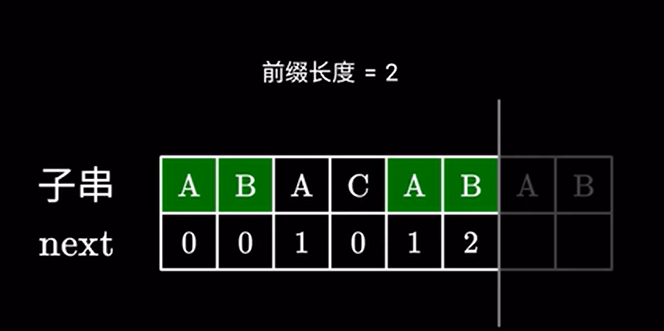
接下来分两种情况讨论，如果下一个字符依然相同：

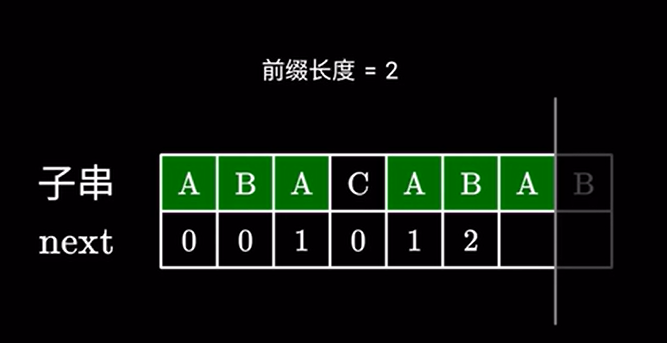
就直接构成了一个更长的前后缀，很显然它的长度等于前面一项加 \(1\) 。

但如果下一个字符不同：

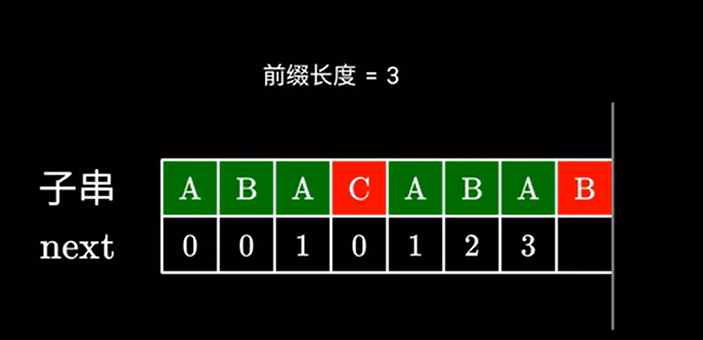
既然 \(ABA\) 无法与下一个字符构成更长的前后缀，

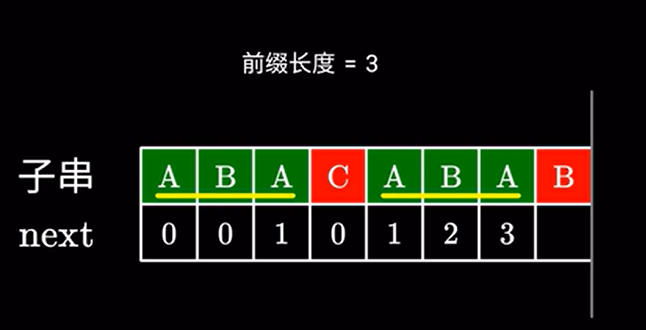
我们就看看是否存在更短的，比如这里的 \(A\) 他其实是有可能与下一个字符构成相同的前后缀的。

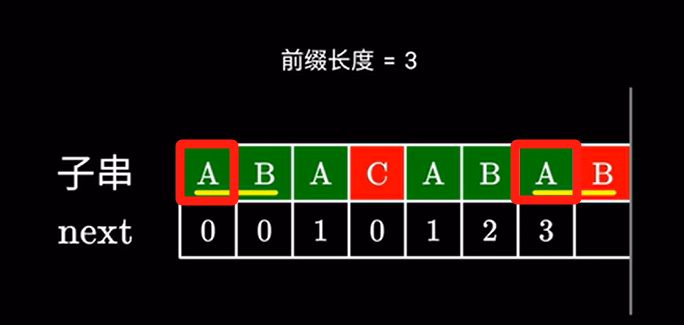
这一步难道要暴力求解？其实不用。

根据之前的计算，我们掌握了一个重要信息，就是字串前后这两部分是相同的。

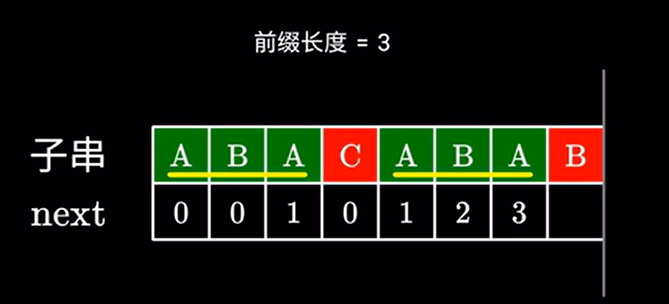
也就是说，右边这部分的后缀等同于左边这部分的后缀，那我们直接在左边这部分查询即可。

左边的前后缀我们之前已经计算过了，查表可得，next值为 \(1\)

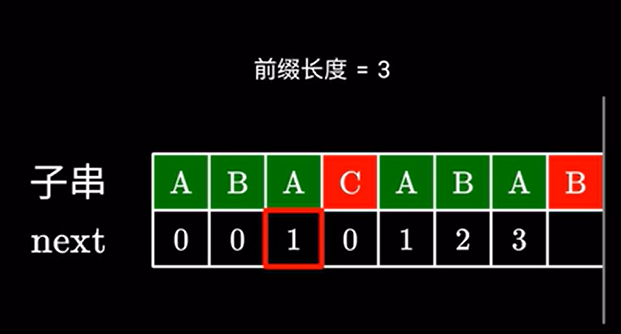
于是我们又回到了最开始的步骤，检查下一个字符是否相同：

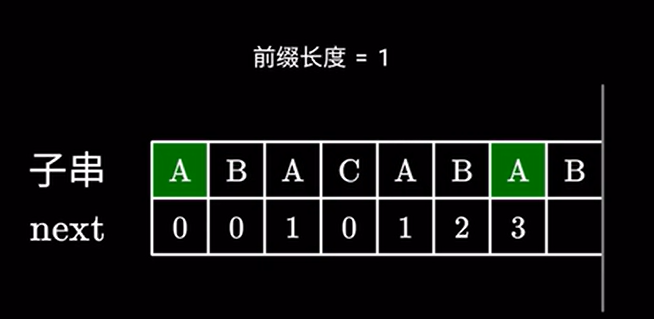
如果相同长度加 \(1\) 即可。

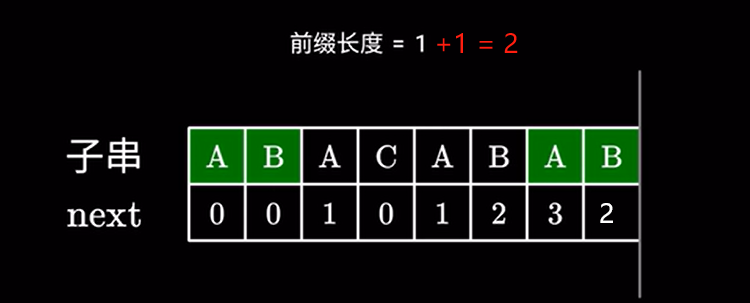
操作正确性

算法实现

我们掌握了next数组的操作原理后，代码就很好实现了。

我们可以采用简单的 \(for\) 和 \(while\) 循环来实现，可以参考以下代码加深理解。

cin>>a>>b;
a='&'+a,b='&'+b;
ll lena=a.size(),lenb=b.size();
nxt[0]=nxt[1]=0;
for(int i=2,j=0;i<lenb;++i){
	while(j&&b[i]!=b[j+1])j=nxt[j];
	nxt[i]=(b[i]==b[j+1])?++j:0;
}

整体实现

来到这一步，我们已经掌握了字符串kmp中90%的部分，只需要最后的利用next数组匹配即可。

注意代码的具体实现可能会有点绕，需仔细理解其每一部分都操作。

可以参考这道题: P3375 【模板】KMP

参考代码（对应上述题目）：

#include<iostream>
#include<cstdio>
#include<string>
using namespace std;
const int N=1e6+10;
#define ll long long
ll nxt[N];
string a,b;
int main(){
	cin>>a>>b;
	a='&'+a,b='&'+b;
	ll lena=a.size(),lenb=b.size();
	nxt[0]=nxt[1]=0;
	for(int i=2,j=0;i<lenb;++i){
		while(j&&b[i]!=b[j+1])j=nxt[j];
		nxt[i]=(b[i]==b[j+1])?++j:0;
	}
	for(int i=1,j=0;i<lena;++i){
		while(j&&a[i]!=b[j+1])j=nxt[j];
		if(a[i]==b[j+1])++j;
		if(j+1==lenb)j=nxt[j],cout<<i-lenb+2<<'\n';
	}
	for(int i=1;i<lenb;++i)cout<<nxt[i]<<' ';
	return 0;
}

参考文献：

1. 基维百科前缀函数与 KMP 算法

2. 最浅显易懂的 KMP 算法讲解

3. 字符串哈希详解