【题解】「UVA11626」Convex Hull

凸包模板题。

之前写过拿 Graham 算法求凸包的，为了不重复/多学点知识，那这次拿 Andrew 算法求凸包吧qaq

*此文章所有图片均为作者手画。

---

Andrew 算法

假设我们有这些点：

首先把所有点以横坐标为第一关键字，纵坐标为第二关键字排序。

相对于 Graham 算法来说，Andrew 算法排序更简单，按 \(x, y\) 坐标排序，时间复杂度也更低（一般的坐标系中排序方法）。

首先将 \(p_1\) 入栈。

然后也将 \(p_2\) 入栈，\(p_2\) 可能在，也可能不在，等着之后判断。

随后，发现 \(p_3\) 偏右，所以我们将 \(p_2\) 出栈。

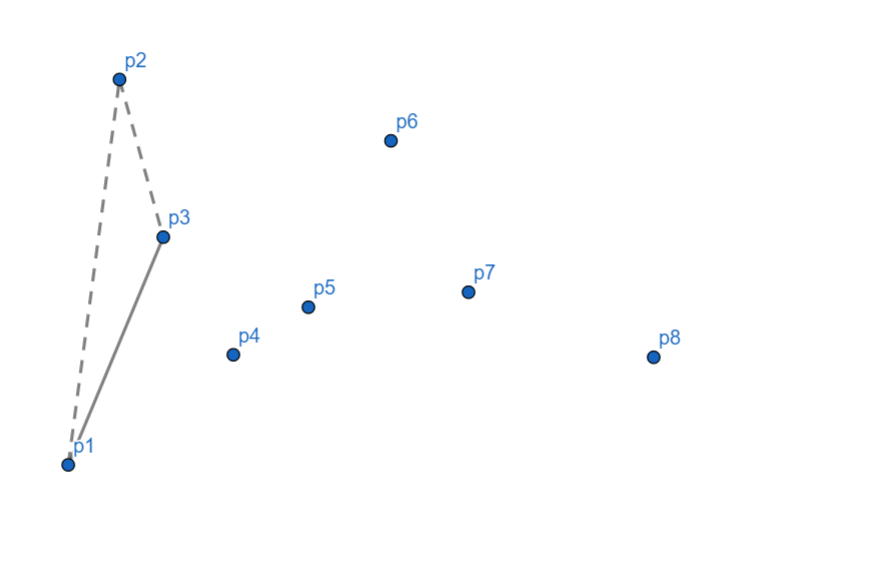
发现 \(p_4\) 依然偏右，\(p_3\) 出栈，\(p_4\) 入栈。

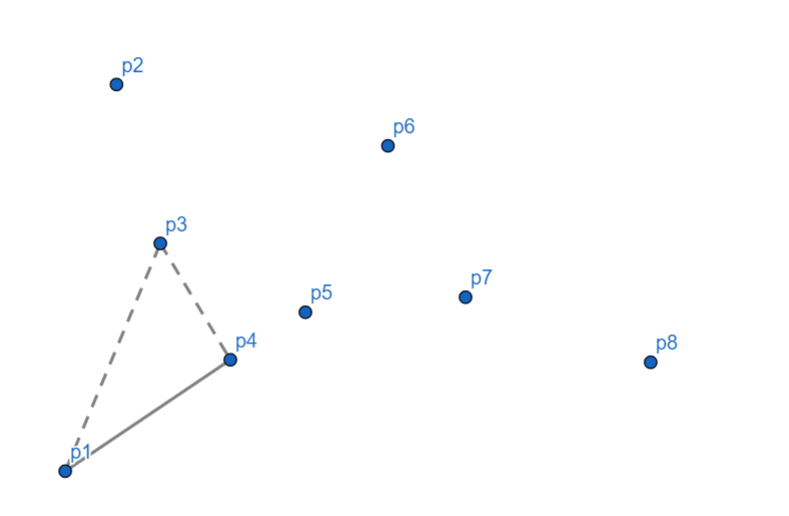
\(p_5\) 向右，\(p_4\) 出栈，\(p_5\) 入栈。

\(p_6\) 向左，入栈。

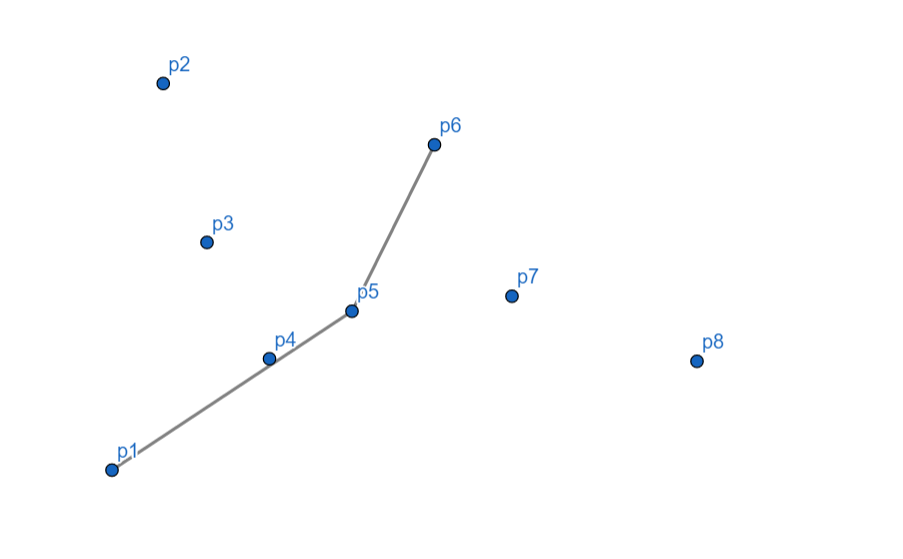
\(p_7\) 向右，\(p_6\) 出栈，\(p_7\) 入栈。

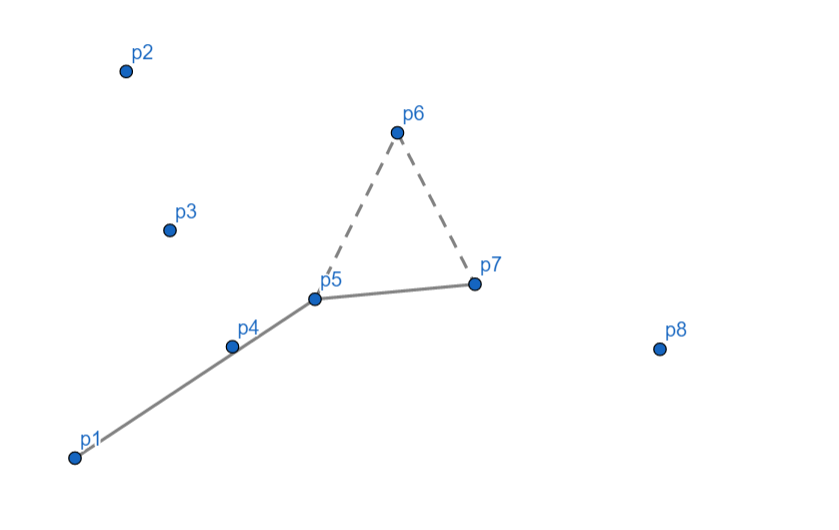
\(p_8\) 向右，\(p_7\) 出栈，继续检查发现相对于 \(p_5\) \(p_8\) 仍然向右，\(p_5\) 出栈，\(p_8\) 入栈。

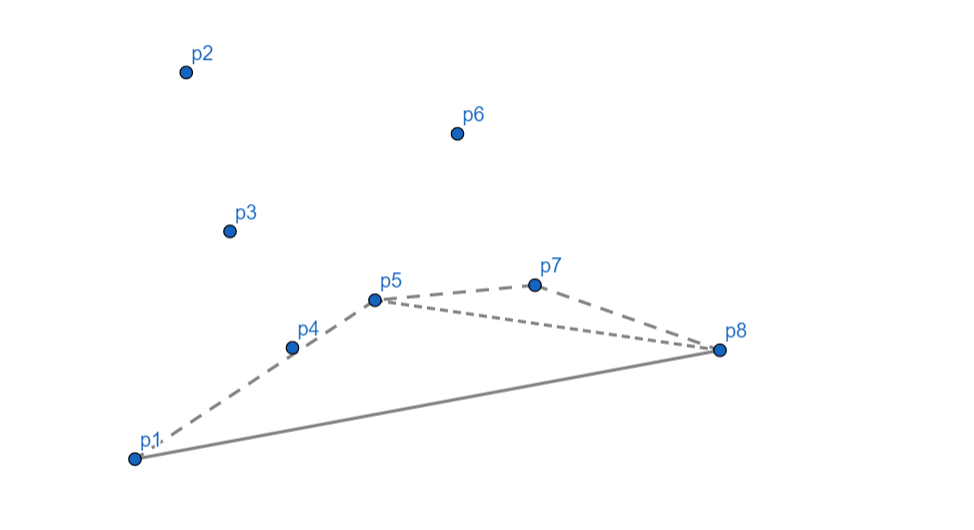
此时，我们发现，凸包明明还空一半就到头了？？？

然而这是意料之中，我们这种算法必然会只算出一半的凸包。

所以我们需要再从排序末尾的点（也就是 \(p_8\)）出发，按照一模一样的方式再算一遍就行了。

当然如果我们走过的点就不许要再走了（除了 \(p_1\)）

从 \(p_8\) 到 \(p_7\)，向左，\(p_7\) 入栈。

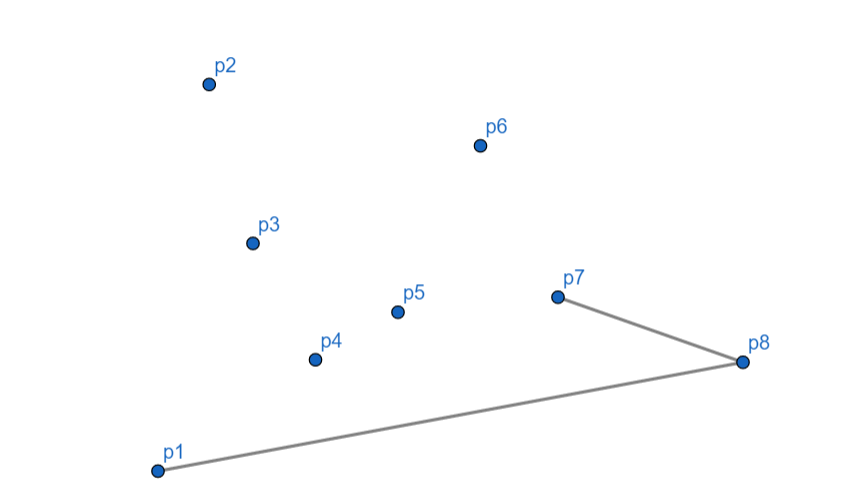
\(p_6\) 向右，\(p_7\) 出栈，\(p_6\) 入栈。

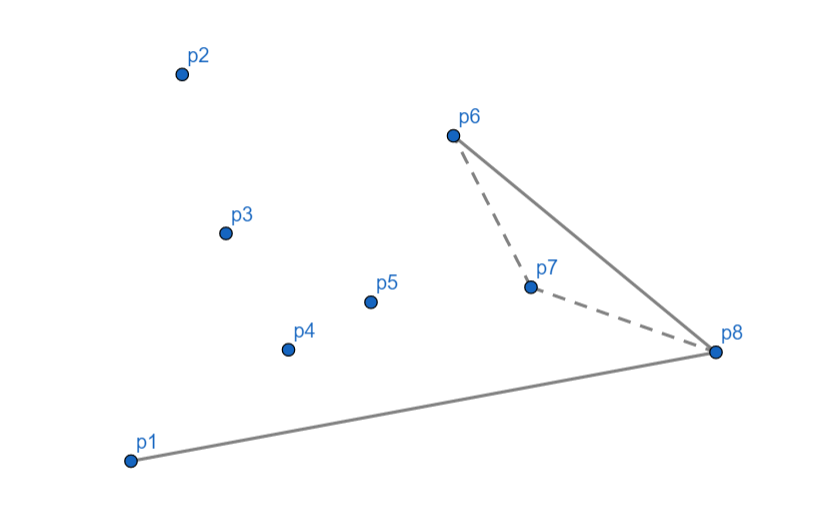
\(p_5\) 向左，入栈。

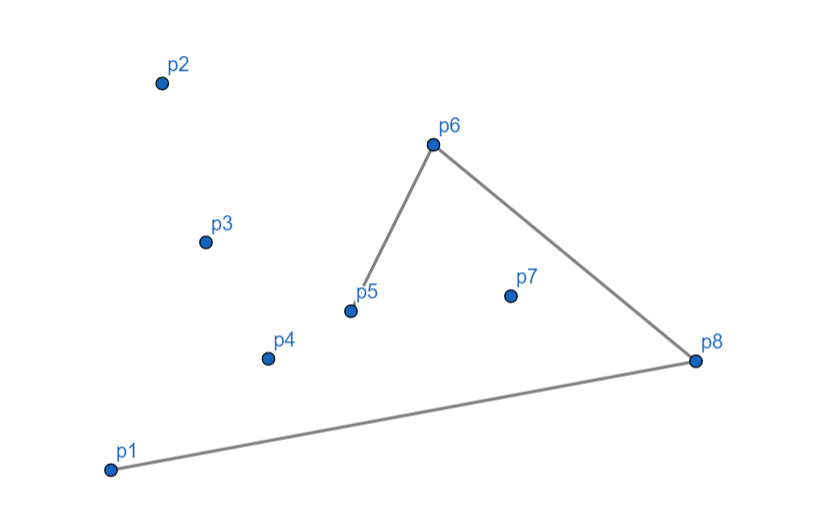
\(p_4\) 向左，入栈。

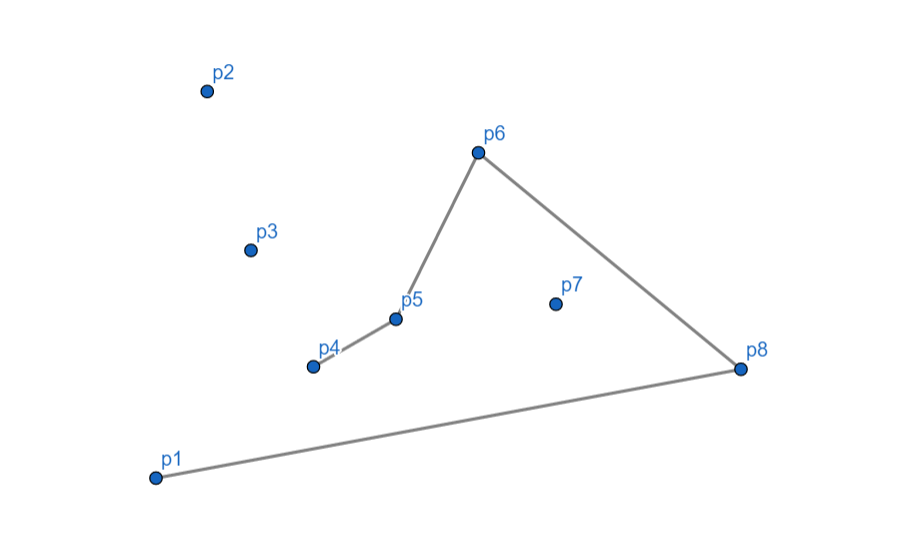
\(p_3\) 向右，\(p_4\) 出栈，对于 \(p_5\) \(p_3\) 依然向右，\(p_5\) 出栈，\(p_3\) 入栈。

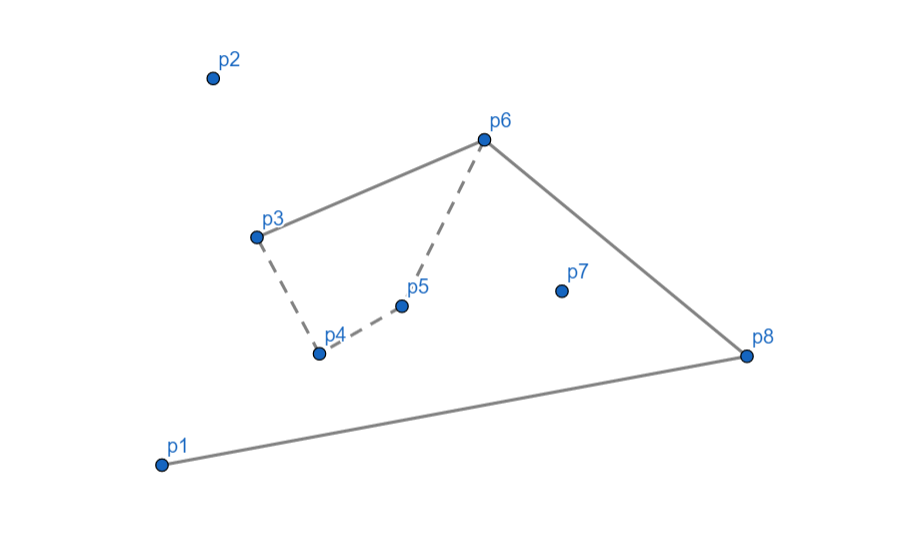
\(p_2\) 向右，\(p_3\) 出栈，\(p_2\) 入栈。

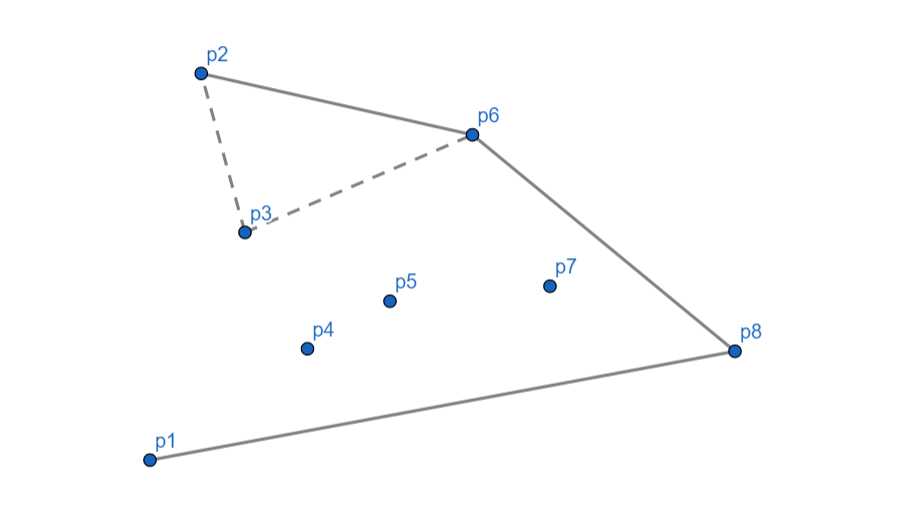
最后将 \(p_2\) 和 \(p_1\) 连起来。

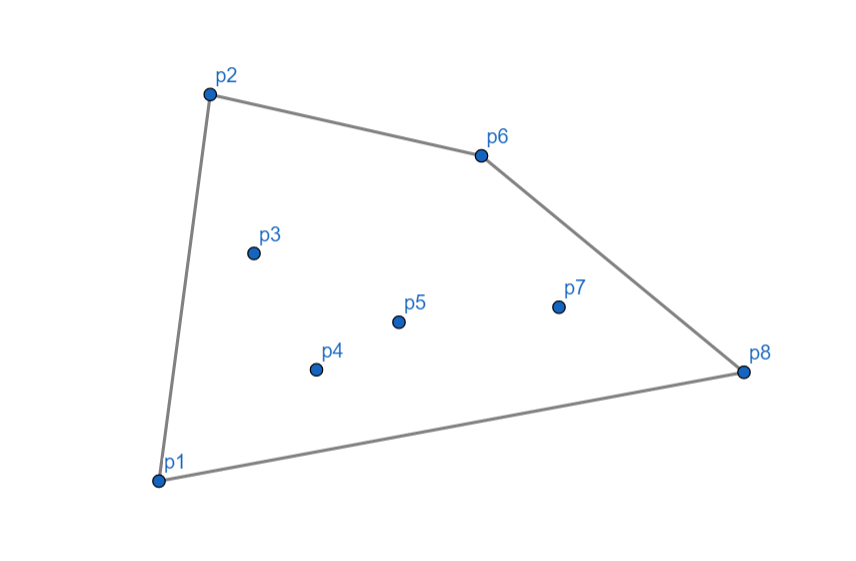
至此，我们的 Andrew 算法就完成了！

扫描的时间复杂度：\(O(n)\)（已过滤常数）

排序时间复杂度：\(O(n \log n)\)

总时间复杂度：\(O(n \log n)\)

---

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<string>
#define line cout << endl
using namespace std;
const int NR = 1e5 + 5;
const double eps = 1e-7;
int n;
struct point {
    double x, y;
    point () {}
    point (double a, double b) : x (a), y (b) {}
    bool operator < (const point &b) const {
        if (x < b.x) return 1;
        if (x > b.x) return 0;
        return y < b.y;
    }
    point operator - (const point &b) {
        return point (x - b.x, y - b.y);
    }
};
point p[NR], sp[NR];
int cmp (double x) {
    if (fabs (x) < eps) return 0;
    return x > 0 ? 1 : -1;
}
double dis (point a, point b) {
    return sqrt ((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
double cp (point a, point b) {
    return a.x * b.y - a.y * b.x;
}
int Andrew () {
    sort (p + 1, p + 1 + n);
    int len = 0;
    for (int i = 1; i <= n; i++) {
        while (len > 1 && cmp (cp (sp[len] - sp[len - 1], p[i] - sp[len - 1])) < 0)
            len--;
        sp[++len] = p[i];
    }
    int k = len;
    for (int i = n - 1; i >= 1; i--) {
        while (len > k && cmp (cp (sp[len] - sp[len - 1], p[i] - sp[len - 1])) < 0)
            len--;
        sp[++len] = p[i];
    }
    return len;
}
int main () {
    int t;
    cin >> t;
    while (t--) {
        cin >> n;
        char c;
        for (int i = 1; i <= n; i++)
            cin >> p[i].x >> p[i].y >> c;
        int t = Andrew();
        cout << t - 1 << endl;
        for (int i = 1; i < t; i++)
            printf ("%.0lf %.0lf\n", sp[i].x, sp[i].y);
    }
    return 0;
}

谢谢qaq