【Notes_9】现代图形学入门——光线追踪(基本原理)

跟着闫令琪老师的课程学习，总结自己学习到的知识点

课程网址GAMES101

B站课程地址GAMES101

课程资料百度网盘【提取码：0000】

目录

• 光线追踪
  • 为什么要光线追踪
    • soft shadow
    • 原因
  • 基本的光线追踪算法（The Basic Ray-Tracing Algorithm）
    • 算法前提:
    • 算法概述
      • 1.Ray Casting
      • 2.Recursive (Whitted-Style) Ray Tracing
  • 线与面的交点
    • 线与面的隐式表示
      • 线的隐式表示
      • 面的隐式表示
    • 光线与面相交
    • 光线与盒子相交
      • Axis-Aligned Bounding Box(AABB) 轴对齐包围盒
    • 加速结构
      • Uniform grids
      • Spatial partitions
      • Object Partitions & Bounding Volume Hierarchy (BVH)

光线追踪

为什么要光线追踪

soft shadow

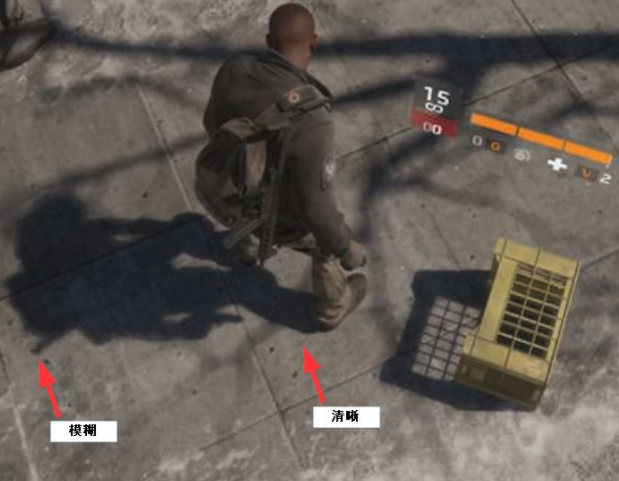
soft shadow相较于hard shadow，其边缘较为模糊。但是我们并不能通过模糊（blur）阴影边界来模拟soft shadow。如下图所示，正确的soft shadow，或者说，符合常理的soft shadow应该表现为，距离投影物体更近的区域，阴影会表现的更清晰。

原因

1. 前面已经学习过光栅化，针对全局光照，我们可以了解到光栅化无法实现或者实现的方法较困难，尤其是有很多的光线共同作用时.

2. 光栅化成像速度很快,但是画质效果不好.光线追踪成像速度慢,但是画质很好

下图1是光栅化,图二是光线追踪

基本的光线追踪算法（The Basic Ray-Tracing Algorithm）

算法前提:

1. 光线是直线传播

2. 不考虑光的波动性

3. 光路互逆性:当你凝视深渊时,深渊也在凝视你.

算法概述

1.Ray Casting

这种算法第一步的简述流程:

1. 视点与每个像素都发射一条光线(射线),射线照射到最近的交点.

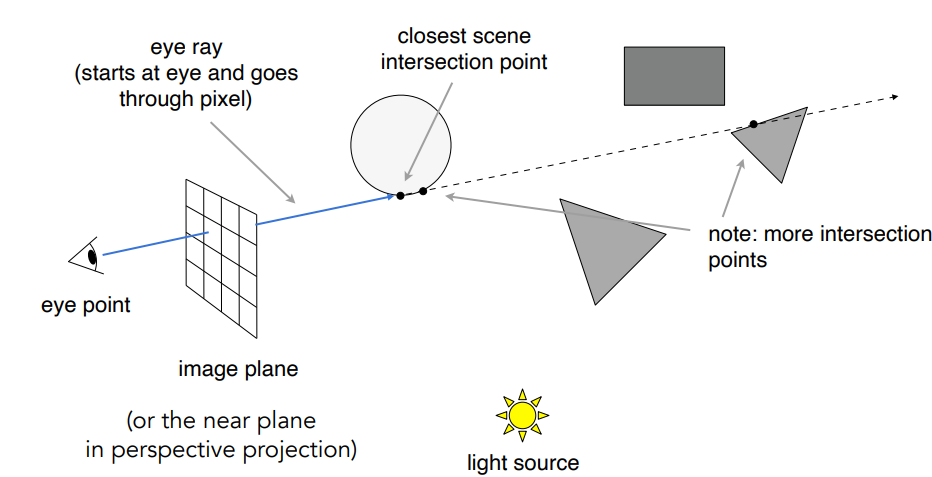
2. 连接交点与光源,判断是否有物体在中间可以知道该交点是否时在阴影中,进行光照模型的计算

2.Recursive (Whitted-Style) Ray Tracing

第一步仅仅实现了光栅化的过程,想要考虑全局光照,就要对全局进行分析.那么第一个交点就会发生光的反射和折射.反射光线与其他物体再相交,也会发生反射和折射现象.交点与光源的连线可以用来检测阴影.

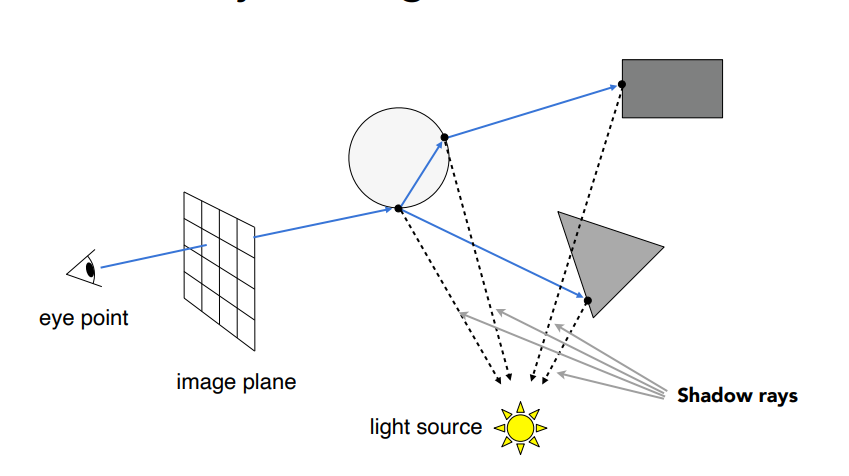
所以每一个交点的颜色来自于直接光照,反射方向间接光照,折现方向的间接光照.

最终实现的效果 :

线与面的交点

线与面的隐式表示

线的隐式表示

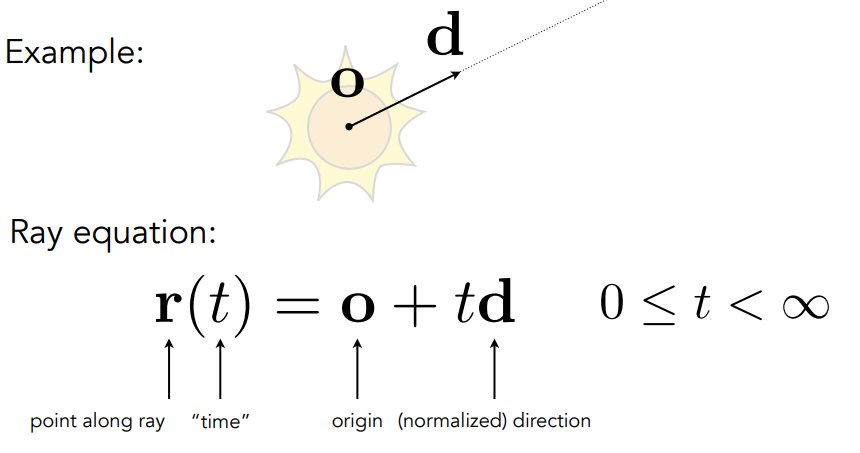
面的隐式表示

光线与面相交

1. 方法一: 等式相等求交点

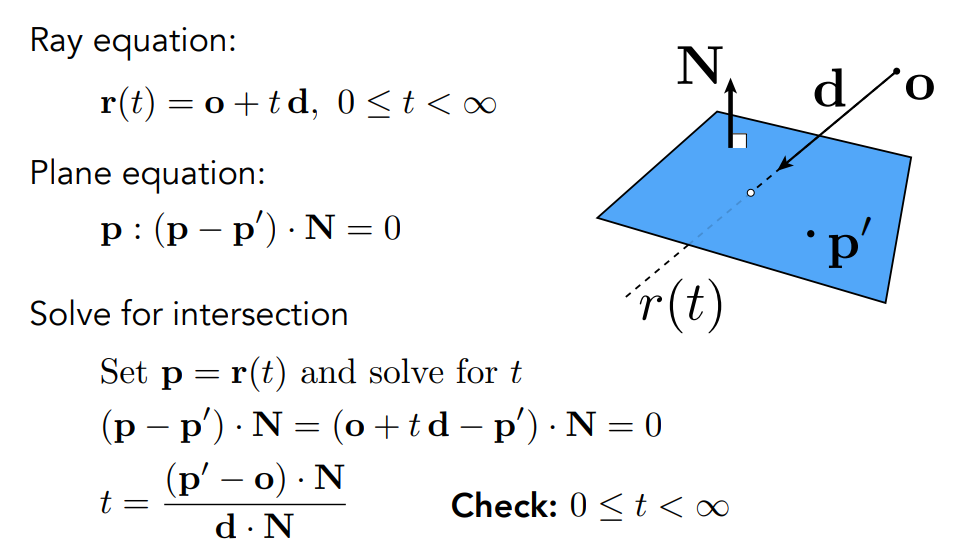
1. 方法二: Möller Trumbore Algorithm

Möller Trumbore Algorithm算法主要是利用重心坐标求解, 具体的实现原理可以算法专栏Möller Trumbore Algorithm

数学原理我们已经知道了,但是具体应用时,如果只是简单的计算模型的每个三角形面与光线是否相交，这样计算的次数有:

\[pixels\times triangles (\times bounces)
\]

太费时，所以通常情况下，我们通常将所有的三角形用box包围其来，这样,我们可以用计算光线与box是否相交，如果光线与box没有交点，那么光线肯定也不会与box内的三角形面相交。如果光线与box有交点，那么再计算光线与box内的三角形是否相交，这样可以节省很多计算量。

基于上面表述,有两个主要的问题：

1. 怎样判断盒子与光线相交

2. 怎么划分盒子,计算量最小(加速结构)

光线与盒子相交

Axis-Aligned Bounding Box(AABB) 轴对齐包围盒

我们可以这样理解光线：光线是一条射线。也可以这样理解一个盒子：盒子是三对平面相交形成的。基于此，AABB盒子就很容易理解了。AABB盒子是平行于\(x,y,z\)轴的平面形成的。

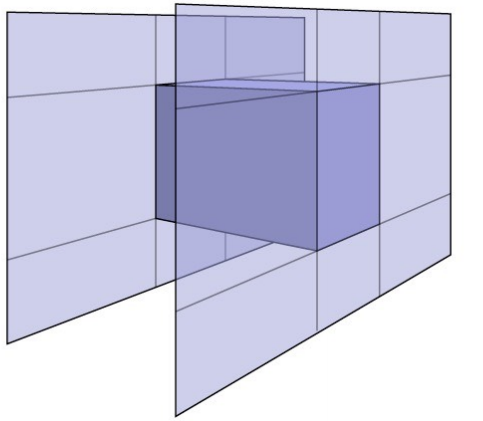
为什么要用AABB盒

计算光线与平面相交的时候更简单

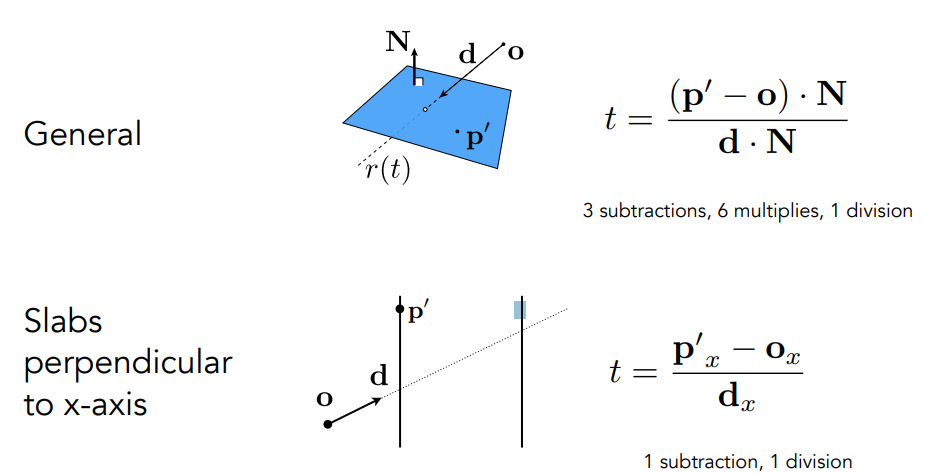
判断AABB盒与光线相交

再看光线与三维box相交之前，我们先从简单二维box的看：光线分别于\(x,y\)平面相交，分别记录照射的时间\(t_{min},t_{max}\)。

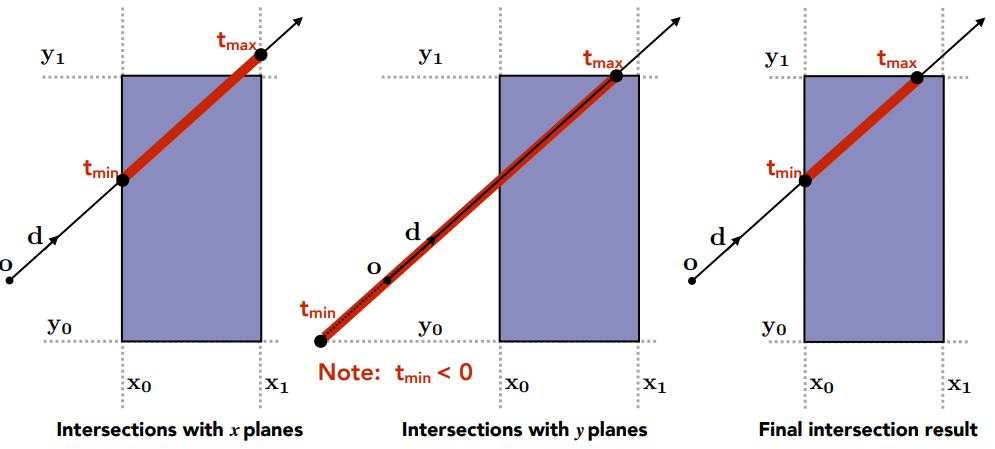
同样的对三维box，也分别对应有三组\(t_{min},t_{max}\)。接下来判断光线与box相交。关键点：

1. 只有当光线进入三组与轴平行的平面才可以判断处光线进入box。

2. 如果光线出任意一个平面，那么光线已经出box了。所以，$$t_{enter} = max(t_{min}) , \quad

t_{exit} = min(t_{max})$$

当\(t_{enter}<t_{exit}\),我们知道光线再box中停留了一段时间。基于此，总结：

1. 当 \(t_{exit}<0\)时，说明光线与box没有交点

2. 当 \(t_{exit}>=0 \quad and \quad t_{enter}<0\)时，说明光线在box内部，与box有交点

3. 当 \(t_{exit}>t_{enter} \quad and \quad t_{exit}>=0\)时，说明光线在box内部，与box有交点

加速结构

通过之前的学习，我们基本上已经实现了Whitted-Style Ray Tracing,但是我们还可以改进算法，来加速光线追踪的速度。

Uniform grids

Spatial partitions

Object Partitions & Bounding Volume Hierarchy (BVH)