week_5

Andrew Ng机器学习笔记---by Orangestar

Week_5

---

重点：反向传播算法，backpropagation

1. Cost Function神经元的代价函数

回顾定义：(上节回顾)

L是☞层数

\(s_l\)指第l层的节点数，注意，该节点数不包含bais偏置项

Ｋ则是输出项的个数。也就是分类的个数

图解回顾：二元分类，多元分类

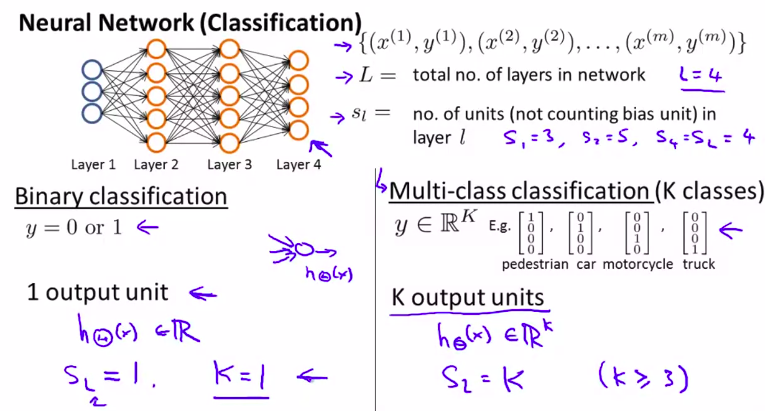
接下来定义神经元的代价函数：

回顾：

逻辑回归中，代价函数（正则化）：

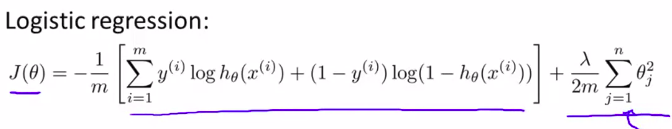
对于神经网络：

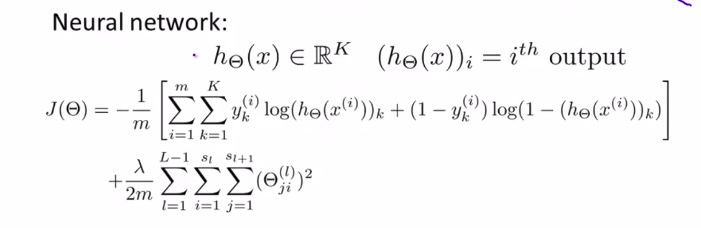
解释：

这其实是一般逻辑回归的代价函数的一般形式。

前面这一大坨，计算的是每一个连线的代价函数，想想那个神经元。所以有２个求和符号。

后一坨，是对于所有的i,j来求和。当然，是每一层。所以有３个求和符号。

原汁原味的解释：

笔记：

• the double sum simply adds up the logistic regression costs calculated for each cell in the output layer.
• the triple sum simply adds up the squares of all the individual \(\Theta\)s in the entire network
• the i in the triple sum does NOT　refer to training example!!!

2. ※　Backprpagation Algorithm　反向传播算法

回顾上节，我们需要计算一个非常复杂的式子，并要对这个式子求最小值：

在本节我们重点讨论如何计算这个偏导项

首先，回顾前向传播算法：

下面，为了计算偏导项，我们需要使用反向传播算法

首先引入一个eroror:

用来计算真实值和假设函数值的差值

\(\delta^{(i)}_j = a^{(i)}_j-y_j\)

这个$ a^{(i)}_j$ 就是\((h_\theta^{(x)})_j\)

注意，这时候，算的是输出层（即最后一层）

毕竟是反向传播算法嘛

当然，可以写成向量形式

\(\delta^{(4)}=a^{(4)}-Y\)

下一步，就要算前面几层的误差了

如图所示:

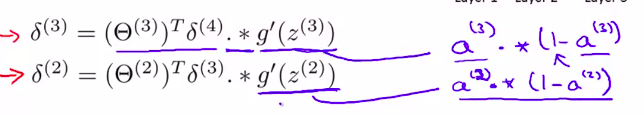
记住ｇ的函数表达式，利用微积分知识很容易证明

当然，要注意的是，这里没有第一层，因为第一层是引入层，输入层，所以不可能有误差

经过十分复杂的证明：

我们可以证明出：

\(\frac\part{\part\theta}J(\theta) = a^{(l)}_j \delta^{(l+1)}_i\)　　这里，我们忽略了标准项

• 那么，如何实现？（很大的训练样本）
  
  基本思路是，先算出所有假设函数，在用训练样本中的值来计算error
  
  

  跳出循环体后，可以计算：
  
  

  然后，就可以计算出偏导项

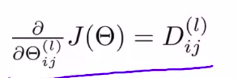
例题：

好难理解啊啊啊啊啊啊

---

再来理一遍!!!:

Back propagation Algorithm

解释：Where L is our total number of layers and $a^{(L)} $is the vector of outputs of the activation units for the last layer. So our "error values" for the last layer are simply the differences of our actual results in the last layer and the correct outputs in y. To get the delta values of the layers before the last layer, we can use an equation that steps us back from right to left:

然后：

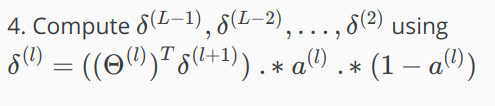
解释：The delta values of layer l are calculated by multiplying the delta values in the next layer with the theta matrix of layer l. We then element-wise multiply that with a function called g', or g-prime, which is the derivative of the activation function g evaluated with the input values given by \(z^{(l)}\).

最后

好的，我知道我理解不了.......

我来偷一下懒：

https://zhuanlan.zhihu.com/p/25081671

https://zhuanlan.zhihu.com/p/25416673

这两篇文章讲的挺好的

3. 反向传播算法－－直观感受

我们先来观察一下，前向传播算法是如何实现的：

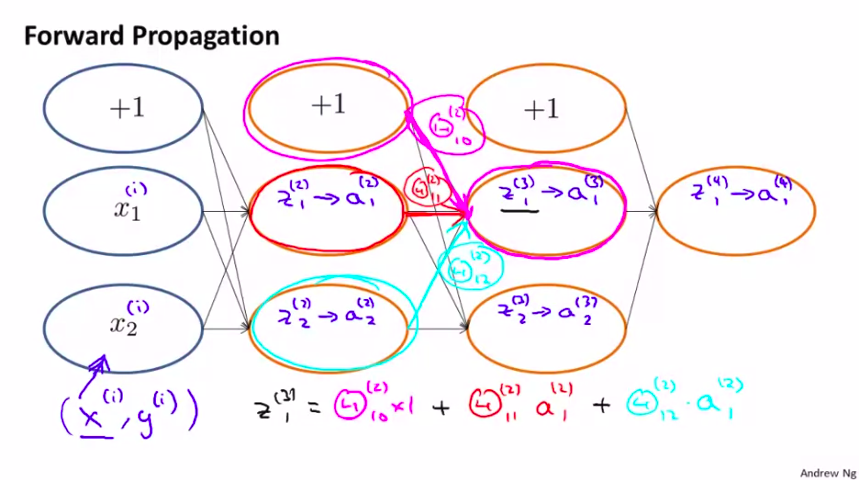
很容易理解。

接下来看看，后向传播算法到底在干嘛？

仔细观察，\delta是如何得到的

前面的误差\delta，由后面的误差来得到

4. 细节实现过程

主要讲如何实现数据向量化

好吧，我没学octave。放过我

例子：

我不会。放过我。

我就截图爽了，混课时长度

5. Gradient Checking

减少算法误差，减少模型错误，bug等

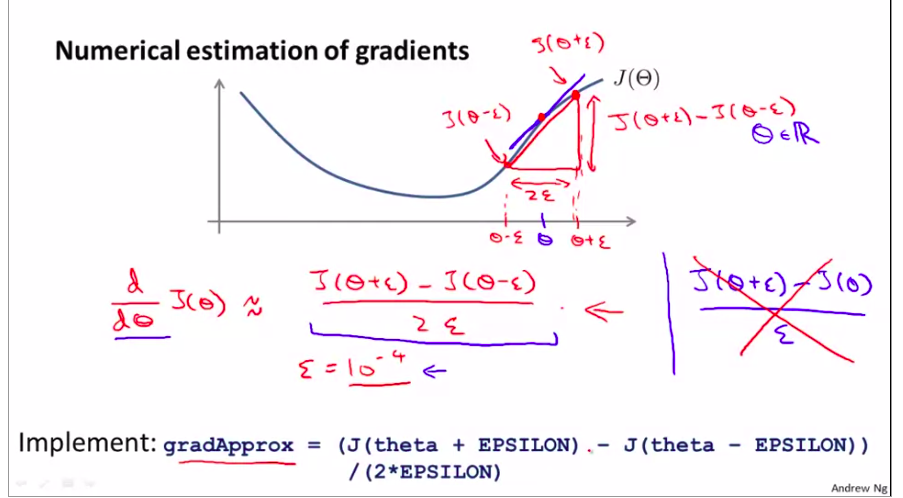
双边导数比单边导数的精度更高

下面看看向量如何来估计？

下面又用octave了。饶了我！

最后，只要确认：

注意：

检测完反向传播算法没问题后，一定要关掉梯度检验！

总结：

本节挺简单的，就是讲了下如何验证反向传播算法的正确性来估计！

6. Random Initialization

随机初始化，我们需要设置随机初始化。很多高级算法都需要

(https://d3c33hcgiwev3.cloudfront.net/imageAssetProxy.v1/y7gaS7pXEeaCrQqTpeD5ng_8868ccda2c387f5d481d0c54ab78a86e_Screen-Shot-2016-12-04-at-11.27.28-AM.png?expiry=1563580800000&hmac=JyszF0nKHl7sZtxzpVzfeMOKskkmga1gdi2K3TGnrkI)

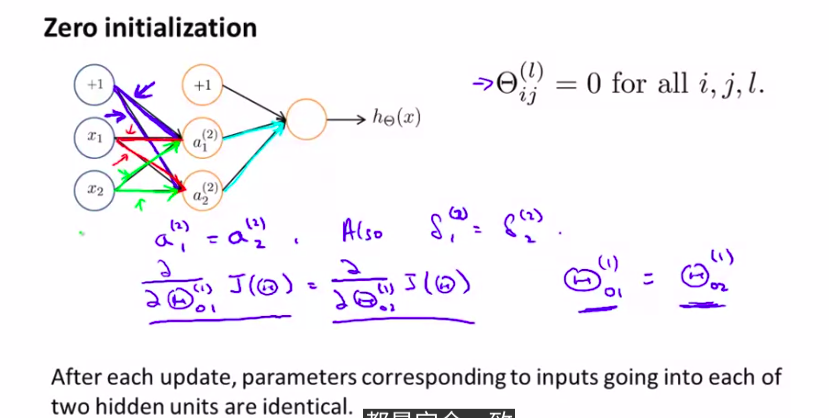
这节学的不是很好》》》》

octave害人

7.Put it Together

---

注明：博客写来完全是给我自己看的！自我满足。

而且，这周学的非常不好，好多知识感觉知识一带而过，

没有真正的理解，有可能是数学知识不够的原因，当然

也可能是最近有些浮躁，为了做笔记而做笔记，急于求成，之类的

希望我自己下次能改进，日后待知识足够，一定要把这周的知识理顺

共勉！