【学习笔记】 Adaboost算法

前言

之前的学习中也有好几次尝试过学习该算法，但是都无功而返，不仅仅是因为该算法各大博主、大牛的描述都比较晦涩难懂，同时我自己学习过程中也心浮气躁，不能专心。

现如今决定一口气肝到底，这样我明天就可以正式开始攻克阿里云天池大赛赛题，所以今天一天必须把Adaboost算法拿下！！！

Adaboost

boosting与bagging

• boosting
  
  个体学习器间存在强依赖关系、必须串行生成的序列化方法，提高那些在前一轮被弱分类器分错的样本的权值，减小那些在前一轮被弱分类器分对的样本的权值，
  
  使误分的样本在后续受到更多的关注。
  
  体现了串行
  
  加法模型将弱分类器进行线性组合
  
  代表模型：Adaboost，GBDT,XGBoost,LightGBM
• bagging
  
  个体学习器不存在强依赖系，可同时生成的并行化方法

Adaboost算法

关于adaboost，我找到了一段非常易懂的描述，具体说来，整个Adaboost 迭代算法就3步：

• 初始化训练数据的权值分布。如果有N个样本，则每一个训练样本最开始时都被赋予相同的权值：1/N。
• 训练弱分类器。具体训练过程中，如果某个样本点已经被准确地分类，那么在构造下一个训练集中，它的权值就被降低；相反，如果某个样本点没有被准确地分类，那么它的权值就得到提高。然后，权值更新过的样本集被用于训练下一个分类器，整个训练过程如此迭代地进行下去。
• 将各个训练得到的弱分类器组合成强分类器。各个弱分类器的训练过程结束后，加大分类误差率小的弱分类器的权重，使其在最终的分类函数中起着较大的决定作用，而降低分类误差率大的弱分类器的权重，使其在最终的分类函数中起着较小的决定作用。换言之，误差率低的弱分类器在最终分类器中占的权重较大，否则较小。
  
  所谓的弱学习器，其实就是之前学的一些模型，比如逻辑斯蒂回归模型，决策树模型，都可以称之为弱学习器。而强学习器，就是以后会接触到的一些神经网络模型，而集成学习的思想，就使用多个弱学习器组合来达成强学习器的思想

算法流程

首先确定一个二分类的训练数据集，然后定义基分类器（弱分类器），例如回归就用cart里的回归树，分类就用cart里的分类树等等，然后开始循环

• 第一步，分为初始化和更新两种可能
  
  1.初始化当前训练数据的权值分布
  
  2.更新，首先是当前分类器所算出的每个样本的权值赋给Dm
  
  
  
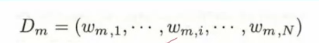
  而这里的w（m，i）实际是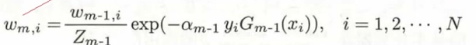
  
  逐步解释一下，首先是分母部分的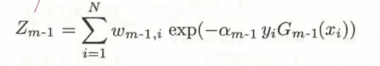，看上去复杂的不得了，实际上是一个归一化操作，为的是让整个分布变成一个概率分布
  
  而对于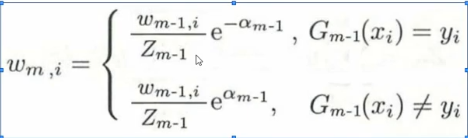，这个式子他简单来说就是一个具有我们所需要的功能的函数，因为我们要的功能很复杂，所以函数设计的很吓人，但是其实我只需要记住她，然后知道他具有能够在分类正确时降低函数值，分类错误时提高函数值，从而达到更新权重的目的
• 第二步，训练当前基分类器
• 第三步，确定权值
  
  1.权值的计算公式简单来说就是如果分类正确就不计入统计，分类错误的话其权值就会被累加计算，而最后算出来的结果记为em，有0≤em≤0.5
  
  2.根据em，计算基分类器的权重系数，给出的公式可以保证当em越小，基分类器的权值越大
  
  
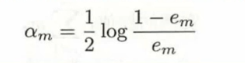
• 第四步，把权值和训练好的分类器放入加法模型
• 第五步，判断是否满足循环条件
  
  1.分类器个数是否达到M
  
  2.总分类器误差率是否满足要求

AdaBoost分类问题的损失函数优化

正如刘老师博客中所说：刚才上一节我们讲到了分类Adaboost的弱学习器权重系数公式和样本权重更新公式。但是没有解释选择这个公式的原因，让人觉得是魔法公式一样。其实它可以从Adaboost的损失函数推导出来。

通过视频 https://www.bilibili.com/video/BV1x44y1r7Zc?p=6 的讲解，自己推了三遍，终于成功！附上稿纸

Adaboost小结

Adaboost的主要优点有：

• Adaboost作为分类器时，分类精度很高
• 在Adaboost的框架下，可以使用各种回归分类模型来构建弱学习器，非常灵活。
• 作为简单的二元分类器时，构造简单，结果可理解。
• 不容易发生过拟合

Adaboost的主要缺点有：

• 对异常样本敏感，异常样本在迭代中可能会获得较高的权重，影响最终的强学习器的预测准确性。

小结

下一篇我会具体的学习GBDT和XgBoost