Webstorm如何配置自动补全前缀--autoprefixer
我们在写样式代码时,对不同平台会有不同的兼容性写法,会在代码前加前缀,但是手动加前缀很费时间而且很容易弄错。Webstorm编辑器是有自带补全前缀功能的,那为什么还要写这篇配置博客,因为Webstorm编辑器并不能把所有的样式代码给你补全,此时加上autoprefixer双剑合璧确保万全。下面是配置步骤:
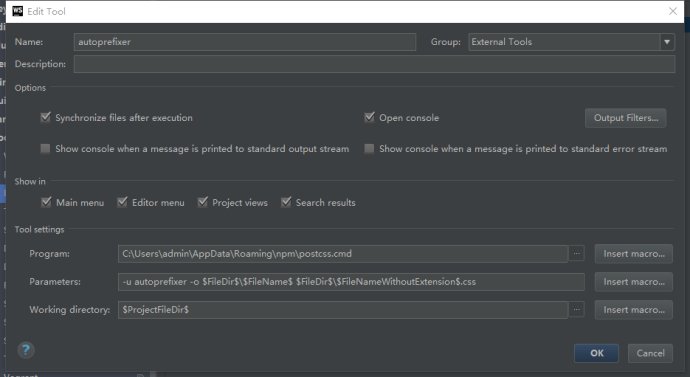
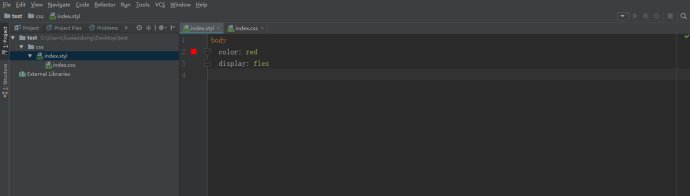
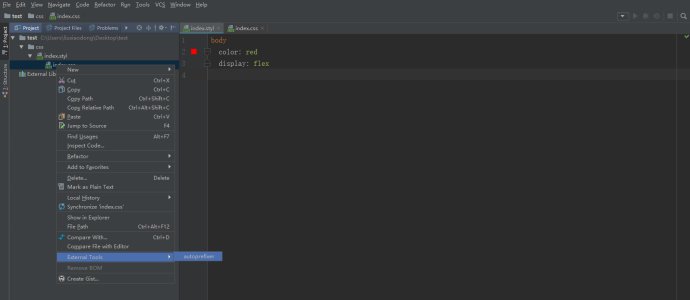
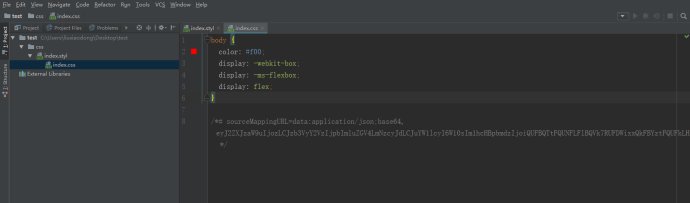
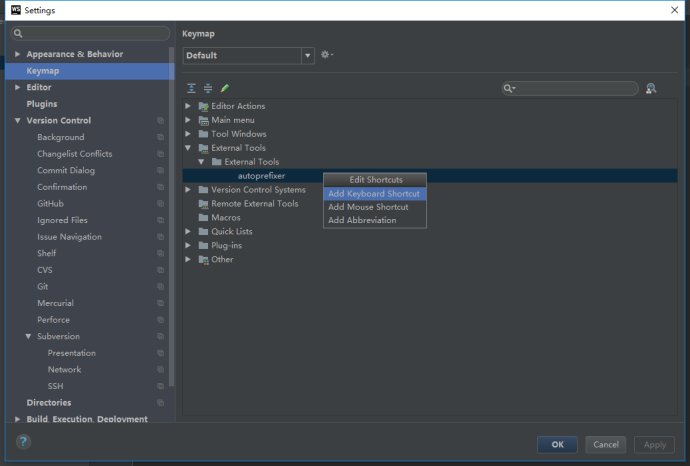
Webstorm如何配置自动补全前缀--autoprefixer的更多相关文章
- Webstorm配置CSS/SCSS自动补全兼容前缀autoprefixer插件
关于Autoprefixer Autoprefixer是一个后处理程序,不象Sass以及Stylus之类的预处理器.它适用于普通的CSS,可以实现css3代码自动补全.也可以轻松跟Sass,LESS及 ...
- 如何配置webpack让浏览器自动补全前缀
一.postcss-loader有什么用? PostCSS 本身是一个功能比较单一的工具.它提供了一种方式用 JavaScript 代码来处理 CSS.它负责把 CSS 代码解析成抽象语法树结构(Ab ...
- 我的Vim配置(自动补全/树形文件浏览)
配置文件的下载路径在这里 http://files.cnblogs.com/files/oloroso/vim.configure.xz.gz 这实际上是一个 xz 格式的文件,添加的 gz 文件后 ...
- 前端css3样式前缀自动补全工具--autoprefixer
最近在学习一份来自git的动画框架源码,看懂70%的核心代码后,打算自己动手实践一版,然鹅,所有框架搭起来以后,在动画这块却出了问题: 想设计一个slideInLeft的动画,必然想到了要从偏移-10 ...
- 【BigData】Java基础_Eclipse配置自动补全new
需求描述 在使用Eclipse的时候,每次new一个对象,写起来比较麻烦,以下是配置Eclipse,然后使用快捷键补全new方法的步骤,此配置使用官方属于叫做:配置自动分配局部变量 配置步骤 打开Wi ...
- termux vim 配置 自动补全 遇到的问题
// 自动不全需要安装 pkg install proot -y // 用proot可以为手机没有root的用户来模拟一个root的环境,这里主要是经典的 Linux 文件系统布局上的模拟. //执行 ...
- EditPlus自动补全、模板配置
EditPlus真的是一款非常好用的编辑器,虽然小,但是短小精悍,速度快.只要配置好了,功能也是很强大的.下面来总结一下如何配置EditPlus的自动补全,和模板配置. 一.配置自动补全:(以开发CS ...
- eclipse代码自动提示设置、如何配置eclipse的代码自动提示功能(同时解决自动补全变量名的问题)?
对于编程人员来说,要记住大量的类名或类方法的名字,着实不是一件容易的事情.如果要IDE能够自动补全代码,那将为我们编程人员带来很大帮助. eclipse代码里面的代码提示功能默认是关闭的,只有输入“. ...
- Vim自动补全神器YouCompleteMe的配置
简介:YouCompleteMe号称Vim的自动补全神器,该项目在github的地址:YouCompleteMe:以下在10.0.1 build-1379776平台配置完成 插件安装操作: 1.确保V ...
随机推荐
- 杂项-Java:Tomcat
ylbtech-杂项-Java:Tomcat 1.返回顶部 1. Tomcat是Apache 软件基金会(Apache Software Foundation)的Jakarta 项目中的一个核心项目, ...
- IDEA中 Spark 读Hbase 报错处理:
SLF4J: Actual binding is of type [org.slf4j.impl.Log4jLoggerFactory] // :: ERROR RecoverableZooKeepe ...
- 19.Extjs主页面显示js
1. /** * @author sux * @time 2011-1-11 * @desc main page */ var mainPage = Ext.extend(Ext.Viewport,{ ...
- 2-4 Vue中的属性绑定和双向数据绑定
<!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...
- justify-content属性
justify-content 用于设置或检索弹性盒子元素在主轴方向上的对齐方式. 属性值:flex-start 属性值:flex-end 属性值:center 属性值:space-between 属 ...
- lodop打印图片
LODOP = getLodop(document.getElementById('LODOP_OB'), document.getElementById('LODOP_EM')); //LODOP. ...
- Ajax 知识点总结
1.AJAX的优缺点都有什么? 最大的一点是页面无刷新,用户的体验非常好.使用异步方式与服务器通信,具有更加迅速的响应能力.可以把以前一些服务器负担的工作转嫁到客户端,利用客户端闲置的能力来处理,减轻 ...
- ACM博弈论总结
一.Bash博弈 1.问题模型:只有一堆n个物品,两人轮流从这堆物品中取物,最多取m个,最后取光者胜. 2.解决思路:当n=m+1时,由于一次最多取m个,无论先取者拿走多少个,后取者都能一次拿走剩余的 ...
- 312 Burst Balloons 戳气球
现有 n 个气球按顺序排成一排,每个气球上标有一个数字,这些数字用数组 nums 表示.现在要求你戳破所有的气球.每当你戳破一个气球 i 时,你可以获得 nums[left] * nums[i] * ...
- 生成清除某个数据库下的所有表的SQL语句
方法1:重建库和表 用mysqldump --no-data把建表SQL导出来,然后drop database再create database,执行一下导出的SQL文件: 方法2:生成清空所有表的SQ ...
