[TJOI2012]桥(最短路+线段树)

有n个岛屿， m座桥，每座桥连通两座岛屿，桥上会有一些敌人，玩家只有消灭了桥上的敌人才能通过，与此同时桥上的敌人会对玩家造成一定伤害。而且会有一个大Boss镇守一座桥，以玩家目前的能力，是不可能通过的。而Boss是邪恶的， Boss会镇守某一座使得玩家受到最多的伤害才能从岛屿1到达岛屿n(当然玩家会选择伤害最小的路径)。问， Boss可能镇守岛屿有哪些。

Solution

我们可以先找出一条最短路，那么我们要删去一条边的话，肯定要从这条路中删。

那么接着考虑一条不在这条路径上的边能够产生的贡献。

看起来有点麻烦，我们可以对于每个不在最短路上的点求一个pre一个nex，大概是这个意思(不太好用文字表述)。

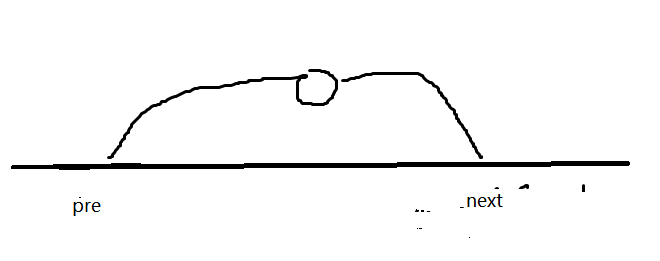
这里的pre是最靠右的，next是最靠左的、

那么这条边能够产生贡献的条件是pre到next中的某条边被删掉。此时的最短路可能为dis[1][x]+l+dis[x][n].。

所以我们要对所有情况取min，这时可以用线段树维护最短路链，区间取min。

Code

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#define N 100002
#define mm make_pair
#define inf 0x3f3f3f3f
using namespace std;
queue<int>q;
int head[N],tot,n,m,dis[][N],pre[N],tr[N<<],la[N<<],ans1,ans2,tag[N],s_t[N],l[N],top,r[N];
bool vis[N],gan[N<<];
struct node{
    int n,to,l;
}e[N<<];
inline void add(int u,int v,int l){
    e[++tot].n=head[u];
    e[tot].to=v;
    e[tot].l=l;
    head[u]=tot;
}
inline void dij(int s,int tag){
    memset(dis[tag],0x3f,sizeof(dis[tag]));
    memset(vis,,sizeof(vis));
    priority_queue<pair<int,int> >q;
    q.push(mm(,s));dis[tag][s]=;
    while(!q.empty()){
        int u=q.top().second;q.pop();
        if(vis[u])continue;vis[u]=;
        for(int i=head[u];i;i=e[i].n){
            int v=e[i].to;
            if(dis[tag][v]>dis[tag][u]+e[i].l){
                dis[tag][v]=dis[tag][u]+e[i].l;pre[v]=u;
                q.push(mm(-dis[tag][v],v));
            }
        }
    }
}
void BFS(int s,int *a,int ta){
    q.push(s);a[s]=s;
    while(!q.empty()){
        int u=q.front();q.pop();
        for(int i=head[u];i;i=e[i].n)if(!a[e[i].to]&&!tag[e[i].to]){
            if(dis[ta][e[i].to]!=dis[ta][u]+e[i].l)continue;
            int v=e[i].to;a[v]=s;q.push(v);
        }
    }
}
inline void pushdown(int cnt){
    if(la[cnt]<tr[cnt<<]){tr[cnt<<]=la[cnt];la[cnt<<]=la[cnt];}
    if(la[cnt]<tr[cnt<<|]){tr[cnt<<|]=la[cnt];la[cnt<<|]=la[cnt];}
    la[cnt]=inf;
}
void upd(int cnt,int l,int r,int L,int R,int x){
    if(l>=L&&r<=R){
        if(x<tr[cnt]){tr[cnt]=x;la[cnt]=x;}
        return;
    }
    int mid=(l+r)>>;
    if(la[cnt]!=inf)pushdown(cnt);
    if(mid>=L)upd(cnt<<,l,mid,L,R,x);
    if(mid<R)upd(cnt<<|,mid+,r,L,R,x);
    tr[cnt]=max(tr[cnt<<],tr[cnt<<|]);
}
void dfs(int cnt,int l,int r){
    if(l==r){
        if(l!=){
        if(tr[cnt]>ans1){ans1=tr[cnt];ans2=;}
        else if(tr[cnt]==ans1)ans2++;
        }
        return;
    }
    int mid=(l+r)>>;
    if(la[cnt]!=inf)pushdown(cnt);
    dfs(cnt<<,l,mid);dfs(cnt<<|,mid+,r);
}
int main(){
    scanf("%d%d",&n,&m);int u,v,w;tot=;
    for(int i=;i<=m;++i){
        scanf("%d%d%d",&u,&v,&w);
        add(u,v,w);add(v,u,w);
    }
    dij(,);int s=n;while(s!=)s_t[++top]=s,tag[s]=top,s=pre[s];s_t[++top]=;tag[]=top;
    dij(n,);
    for(int i=;i<=n;++i)
      for(int j=head[i];j;j=e[j].n){
          int v=e[j].to;
          if(dis[][i]+dis[][v]+e[j].l==dis[][n]&&tag[i]&&tag[v])gan[j]=gan[j^]=;
     }
    for(int i=;i<=top;++i)BFS(s_t[i],l,);    //t->s
    for(int i=top;i>=;--i)BFS(s_t[i],r,);    //s->t
    memset(tr,0x3f,sizeof(tr));memset(la,0x3f,sizeof(la));
    for(int i=;i<=n;++i)
      for(int j=head[i];j;j=e[j].n)if(!gan[j]&&tag[l[i]]>tag[r[e[j].to]]){
          int v=e[j].to;
      //    cout<<tag[r[v]]+1<<" "<<tag[l[i]]<<" "<<dis[0][i]+e[j].l+dis[1][v]<<endl;
          upd(,,top,tag[r[v]]+,tag[l[i]],dis[][i]+e[j].l+dis[][v]);
      }
    dfs(,,top);if(ans1==dis[][n])ans2=m;
    cout<<ans1<<" "<<ans2<<endl;
    return ;
}