BZOJ 1064 假面舞会

http://www.lydsy.com/JudgeOnline/problem.php?id=1064

思路:第一眼看的时候以为是差分约束，但是是做不了的，不过能保证的就是这题绝对是图论题。。。(废话)

分联通块考虑，如果每个联通块都是没有有向环的话，那么各个联通块中，最长链就是最大答案，3就是最小答案。

只要有一个联通块有环，那么答案一定是这个环长度的因数，最大答案，就是这些环长度的gcd

不过，要是有这个非正常的环怎么办?

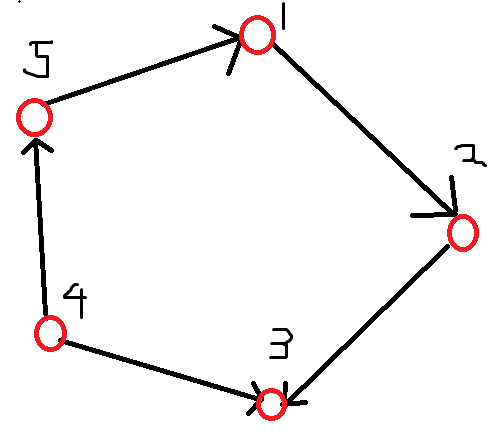
我们可以看到,4->3和2->3都指向了3，这怎么办？那么我们只要在一开始建图的时候，原来的有向边权值为1，再同时建一个反向边权值为-1，把有向图变成无向图。

为什么?，因为如图，4可以到3,2也可以到3，说明2的编号和4相同，所以2->3->4的路径实际上是"走出去一步，又走回来一步"，也就是我常说的"有来有回",按照我们刚才的建图方式，这个环的长度就是:1+1+1+1-1=3，事实上，答案也是如此，3和5编号相同，2和4编号相同，这样图中实际上是只有3种面具。

 #include<algorithm>
 #include<cstdio>
 #include<cmath>
 #include<cstring>
 #include<iostream>
 int tot,go[],next[],first[];
 int c[],dis[],vis[],n,m,len,val[];
 int read(){
     int t=,f=;char ch=getchar();
     while (ch<''||ch>''){if (ch=='-') f=-;ch=getchar();}
     while (''<=ch&&ch<=''){t=t*+ch-'';ch=getchar();}
     return t*f;
 }
 void insert(int x,int y,int z){
     tot++;
     go[tot]=y;
     next[tot]=first[x];
     first[x]=tot;
     val[tot]=z;
 }
 void add(int x,int y){
     insert(x,y,);insert(y,x,-);
 }
 int gcd(int a,int b){
     if (b==) return a;
     else return gcd(b,a%b);
 }
 int bfs(int x){
     int h=,t=;c[]=x;vis[x]=;dis[x]=;
     int mxdis=,mndis=;
     while (h<=t){
         int now=c[h++];
         for (int i=first[now];i;i=next[i]){
             int pur=go[i];
             if (vis[pur]){
                 len=gcd(len,val[i]+dis[now]-dis[pur]);
                 continue;
             }
             vis[pur]=;
             c[++t]=pur;
             dis[pur]=dis[now]+val[i];
             mxdis=std::max(mxdis,dis[pur]);
             mndis=std::min(mndis,dis[pur]);
         }
     }
     return mxdis-mndis+;
 }
 int main(){
     n=read();m=read();
     for (int i=;i<=m;i++){
         int x=read(),y=read();
         add(x,y);
     }
     int sum=;
     for (int i=;i<=n;i++)
      if (!vis[i]) sum+=bfs(i);
     len=std::abs(len);
     if (len){
         if (len<) {
             printf("-1 -1\n");
             return ;
         }
         printf("%d ",len);
         for (int i=;i<=len;i++)
          if (len%i==) {
                 printf("%d\n",i);
                 break;
          }
         return ;
     }else
     if (sum<){
         printf("-1 -1\n");
         return ;
     }else{
         printf("%d 3\n",sum);
         return ;
     }
 }