浮点数与快速log2

请先于浮点数的文章：http://blog.jobbole.com/86371/

先贴一张关于float和double的图：

float:

double: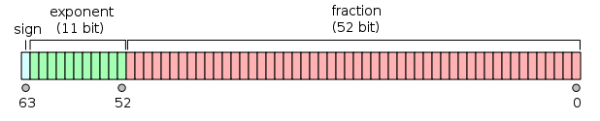

快速log2长这样：

 int flog2(float x) {
     return ((unsigned&)x>>&)-;
 }

由于float是这样储存数的：一个字节的符号位，8个字节的指数，还有23个字节的基数。指数以127为偏移量，以2为基。基数以2进制表示。一个float就是：

符号*2^指数-127*(1+基数*2^-23)

因此，float能表示的范围是2^-127到2¹²⁷，但是只有lg（2²³）+1≈7位有效数字。

我们发现，这个float的log就是指数-127。。

于是我们可以解释flog2了。(unsigned&)表示将x的地址看做是unsigned int（暂不知道原理），这样x才能右移。接着，x右移23位，表示舍弃基位。然后x&255，表示舍弃符号位（因为x不能为负数）。最后减去偏移量127，就是log了。

但是float不是只有7位有效数字吗？万一精度损耗怎么办？事实上对于任何127位以内的整数（c++内置最大64位），flog2都能求出正确答案。因为一个正整数log2的值一定由它的最高位位置决定，而在转换时最高位一定会被当做整数部分中的1，不会被舍弃，所以求出来的值一定正确。