【bzoj1965】: [Ahoi2005]SHUFFLE 洗牌 数论-快速幂-扩展欧几里得

【bzoj1965】: [Ahoi2005]SHUFFLE 洗牌

观察发现第x张牌

当x<=n/2 x=2x

当x>n/2 x=2x-n-1

好像就是 x=2x mod (n+1)

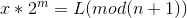 就好了

 /* http://www.cnblogs.com/karl07/ */
 #include <cstdlib>
 #include <cstdio>
 #include <cstring>
 #include <cmath>
 #include <algorithm>
 using namespace std;
 #define LL long long
 
 LL n,m,l,g,x,y;
 
 LL gcd(LL a,LL b){return !b ? a : gcd(b,a%b);}
 
 void ex_gcd(LL a,LL b,LL &x,LL &y){
     if (b==){x=; y=; return;}
     ex_gcd(b,a%b,y,x);
     y-=x*(a/b);
 }
 
 LL Q_pow(LL x,LL y){
     LL ans=;
     while(y){
         if (y&) ans=ans*x%(n+);
         x=x*x%(n+);
         y=(y>>);
     }
     return ans;
 }
 
 int main(){
     scanf("%lld%lld%lld",&n,&m,&l);
     m=Q_pow(,m);
     g=gcd(n+,m);
     ex_gcd(m/g,(n+)/g,x,y);
     x=x*(l/g)%(n+);
     printf("%lld\n",(x+(n+))%(n+));
     return ;
 }