AI 高等数学、概率论基础
一、概论
基础引入:
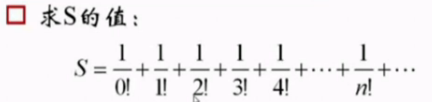
原理一:【两边夹定理】
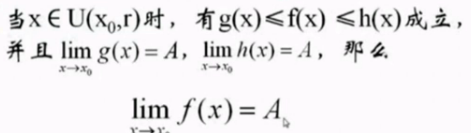
原理二:【极限】

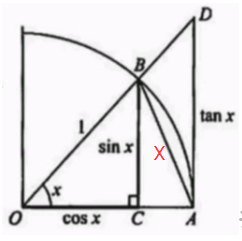
X为角度x对应的圆弧的点长;
原理三【单调性】:

引入:


二、导数

常见函数的导数:

四、应用:

求解:

泰勒展式和麦克劳林展式:

泰勒展式在x0 = 0处展开得到麦克劳林展式
Taylor公式的应用1:

变种:

Taylor公式应用2:
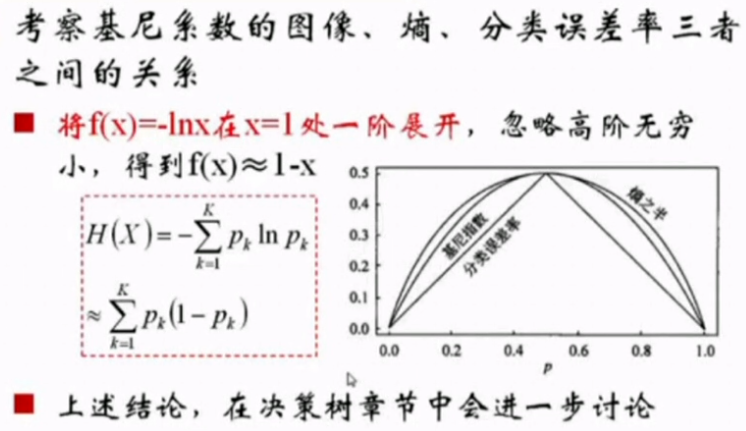
方向导数:

梯度:

函数的凸凹性:

函数凸凹性判定:


凸函数性质的应用:
 、
、

五、概率论

概率为0例子: 把一枚针投在一个平面上,则概率为0(一个点 之于 一个面)
古典概型:

思路:

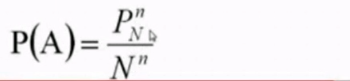
古典概型变种问题:
生日悖论:


古典概型总结:

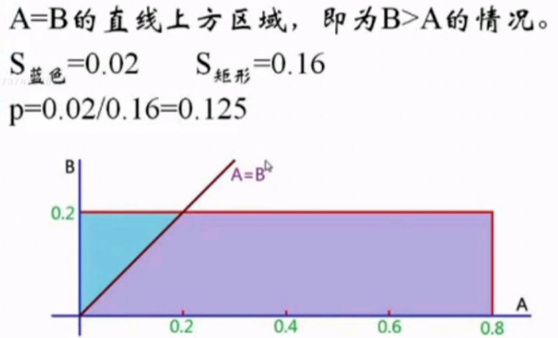
几何概型:

条件概率:
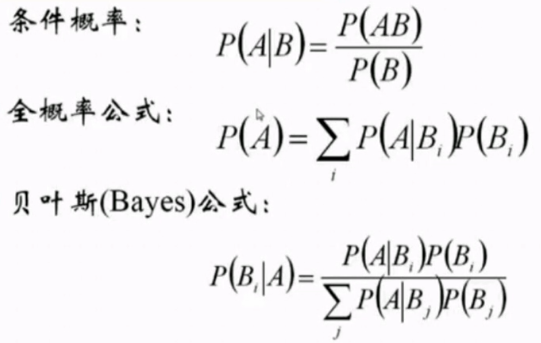
条件概率: 在已知B发送的条件下,A发生的概率
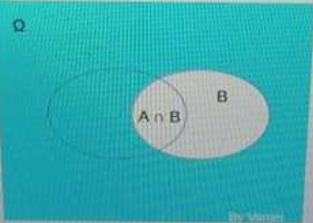
全概率:

全概率公式的意义在于: 当直接计算P(A)比较困难,而P(Bi),P(A|Bi) (i=1,2,...)的计算较为简单时,可以利用全概率公式计算P(A)。思想就是,将事件A分解成几个小事件,通过求小事件的概率,然后相加从而求得事件A的概率,而将事件A进行分割的时候,不是直接对A进行分割,而是先找到样本空间Ω的一个个划分B1,B2,...Bn,这样事件A就被事件AB1,AB2,...ABn分解成了n部分,即A=AB1+AB2+...+ABn, 每一Bi发生都可能导致A发生相应的概率是P(A|Bi),由加法公式得
P(A)=P(AB1)+P(AB2)+....+P(ABn)
=P(A|B1)P(B1)+P(A|B2)P(B2)+...+P(A|Bn)P(PBn)
贝叶斯公式:
与全概率公式解决的问题相反,贝叶斯是建立在条件概率的基础上寻找事件发生的原因(即大事件A已经发生的条件下,分割中的小事件Bi的概率),设B1,B2,...是样本空间Ω的一个划分,则对任一事件A(P(A)>0),有

Bi 常被视为导致试验结果A发生的”原因“,P(Bi)(i=1,2,...)表示各种原因发生的可能性大小,故称先验概率;P(Bi|A)(i=1,2...)则反映当试验产生了结果A之后,再对各种原因概率的新认识,故称后验概率。
贝叶斯公式的应用:

 、
、
两学派的认知:【频率学派 && 贝叶斯学派】

贝叶斯公式扩展:

两点分布:

二项分布:【伯努力分布】



泊松分布【Taylor展式结合】:



泊松分布的应用:

连续分布之均匀分布:

连续分布之指数分布:


指数分布的无记忆性:

连续分布之正态分布【高斯分布】:


总结:
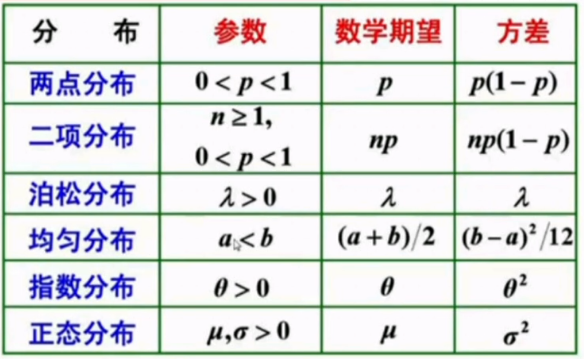
指数族:
二项分布【伯努力分布】,正态分布【高斯分布】属于指数族
logistic函数【sigmod函数】:
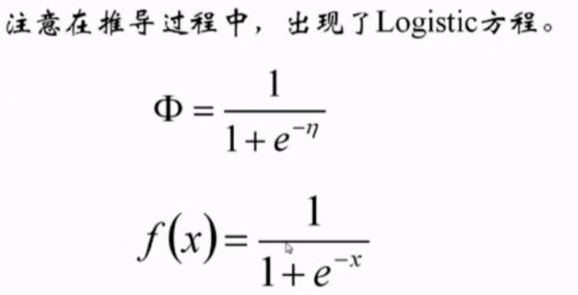

Logistic函数的导数:
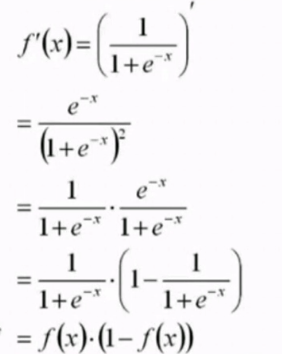
期望:

期望的性质:

note: P(xy) = P(x) P(y) --> x, y独立
方差:

协方差:

协方差、独立、不相关关系:

协方差的意义:

协方差的上界:


独立一定不相关,不相关不一定独立,不相关只是线性独立,可能是非线性不独立;
相关系数:

其中:Var(x): 标准差;
协方差矩阵:

原点矩 和 中心矩

期望为一阶原点矩, 方差为2阶中心矩
概念总结:

偏度:


偏度为0, 则是正态分布
偏度公式:

峰度:

应用:


引入切比雪夫不等式:

大数定理:


中心极限定理:

标准的中心极限定理的问题:


中心极限定理的意义:

样本的统计量:

样本的矩:

随机变量的矩 和 样本的矩, 有什么关系呢??

矩估计:【非常重要】


正态分布的矩估计:

均匀分布的矩估计:

贝叶斯公式带来的思考:

最大似然估计:

极大似然估计的具体实践:

极大似然估计的应用:


正态分布的极大似然估计:


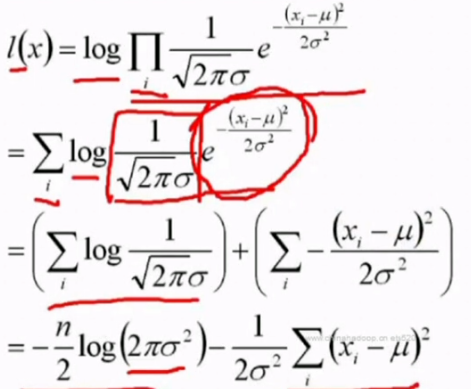

总结:

极大似然估计与过拟合:

5、 10 为超参数;
AI 高等数学、概率论基础的更多相关文章
- PGM:概率论基础知识
http://blog.csdn.net/pipisorry/article/details/52459847 概率图模型PGM:概率论基础知识 独立性与条件独立性 独立性 条件独立性 也就是表示给定 ...
- 新手立体四子棋AI教程(1)——基础扫盲
一.引言 最近身边好几个朋友开始玩立体四子棋,激起了我的好奇心.那么首先来说什么是[立体四子棋],规则又是如何呢? 上图即为立体四子棋,规则类似于五子棋四子连在一起,但是四子棋更加多样.丰富.不仅可以 ...
- 概率论基础教程 (Sheldon M. Ross 著)
第1章 组合分析 1.1 引言 1.2 计数基本法则 1.3 排列 1.4 组合 1.5 多项式系数 *1.6 方程的整数解个数 第2章 概率论公里 2.1 引言 2.2 样本空间和事件 2.3 概率 ...
- 读书笔记:Sheldon Ross:概率论基础教程:随机变量
例1b 一个坛子里装有编号1-20的球,无放回抽取3个,取出球中至少一个号码大于等于17的概率是多少? 除了书上的解法外,还有一种解法: 考虑相反的情况:三个球的号码都小于17. 第一次从编号1-16 ...
- 读书笔记:Sheldon.M.Ross:概率论基础教程:2014.01.22
贝叶斯公式与全概率公式 全概率公式:如果一件事情的发生有多个可能途径,那么这件事情的发生概率就是在不同途径下此事件发生的条件概率的加权平均.权值为各途径本身的发生概率. 贝叶斯公式:通过例子说明其含义 ...
- 概率论基础知识(Probability Theory)
概率(Probability):事件发生的可能性的数值度量. 组合(Combination):从n项中选取r项的组合数,不考虑排列顺序.组合计数法则:. 排列(Permutation):从n项中选取r ...
- AI人工智能顶级实战工程师 课程大纲
课程名称 内容 阶段一.人工智能基础 — 高等数学必知必会 1.数据分析 "a. 常数eb. 导数c. 梯度d. Taylore. gini系数f. 信息熵与组合数 ...
- 想做AI测试,需要学习哪些数学知识?
摘自知乎的回答 作者:者也 以上是个人读研以来感受用得最多的数学基础课,挂一漏万,大侠请补充指正 高等数学是基础中的基础,研究生以上级别的一切理工科都需要这个打底,数据挖掘.人工智能.模式识别此类跟数 ...
- MMORPG大型游戏设计与开发(服务器 AI 控制器)
上一篇我们说了基础接口的组成,想必大家对AI中的基础方法有了一定的了解,而基础接口只能一个通用的,要实现不同的类别还需子类中实现,这就形成了玩家.主动.被动.木桩这些类型.不同类型的AI需要有一个统一 ...
随机推荐
- 面试题04_替换空格_剑指Offer系列
题目描写叙述 请实现一个函数,将一个字符串中的空格替换成"%20". 比如,当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy. 解题思路 ...
- 【Python】torrentParser1.03
#------------------------------------------------------------------------------------ # torrentParse ...
- 【Python】torrentParser1.01
在昨天的版本上做了一些改进,如增加getAll,修改getSingleFileName等 代码: #-------------------------------------------------- ...
- CentOS7安装Docker与使用篇
一.在CentOS7上安装Docker篇 1. 查看系统版本: $ cat /etc/redhat-release CentOS Linux release 7.0.1406 (Core) 2. 安装 ...
- CSS外框高度自动适应
当有浮动float时,最外框会不跟随内容的高度而高: 解决办法一:清除浮动 clear:both <!DOCTYPE html> <html xmlns="http:// ...
- SQL Server 中断开连接到指定数据库的所有连接
常用的情形是在部署测试数据库时需要通过SQL代码自动重新创建数据库,在删除的时候往往会发生错误,错误信息一般会指出目前有用户连接到这个数据库上,因此不能删除. 实现的方式是通过查询指定数据库中活跃的 ...
- Centos7中安装Python3
环境:CentOS 7 1. 安装依赖环境 # yum -y install zlib-devel bzip2-devel openssl-devel ncurses-devel sqlite-dev ...
- C++ 第六课:C/C++关键字及其用法
asm 插入一个汇编指令. auto 声明一个本地变量. bool 声明一个布尔型变量. break 结束一个循环. case 一个switch语句的一部分. catch 处理 thrown 产生的异 ...
- Go语言使用Beego的ORM插入Mysql后,时区不一致的解决方案
一.解决方案: 方案一: orm.Debug = false orm.DefaultTimeLoc = time.UTC orm.RegisterDriver("mysql", o ...
- kafka性能测试(转)KAFKA 0.8 PRODUCER PERFORMANCE
来自:http://blog.liveramp.com/2013/04/08/kafka-0-8-producer-performance-2/ At LiveRamp, we constantly ...
